|
协方差矩阵在统计学和机器学习中随处可见,一般而言,可视作方差和协方差两部分组成,即方差构成了对角线上的元素,协方差构成了非对角线上的元素。本文旨在从几何角度介绍我们所熟知的协方差矩阵。
1.方差和协方差的定义
在统计学中,方差是用来度量单个随机变量的离散程度,而协方差则一般用来刻画两个随机变量的相似程度,其中,方差的计算公式为 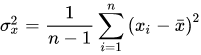 其中,
n
n
n 表示样本量,符号
x
‾
\overline x
x 表示观测样本的均值,这个定义在初中阶段就已经开始接触了。 在此基础上,协方差的计算公式被定义为 其中,
n
n
n 表示样本量,符号
x
‾
\overline x
x 表示观测样本的均值,这个定义在初中阶段就已经开始接触了。 在此基础上,协方差的计算公式被定义为 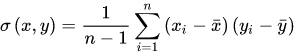 在公式中,符号
x
‾
\overline x
x,
y
‾
\overline y
y 分别表示两个随机变量所对应的观测样本均值,据此,我们发现:方差
σ
x
2
\sigma_x^2
σx2可视作随机变量
x
x
x关于其自身的协方差
σ
(
x
,
x
)
\sigma(x,x)
σ(x,x). 在公式中,符号
x
‾
\overline x
x,
y
‾
\overline y
y 分别表示两个随机变量所对应的观测样本均值,据此,我们发现:方差
σ
x
2
\sigma_x^2
σx2可视作随机变量
x
x
x关于其自身的协方差
σ
(
x
,
x
)
\sigma(x,x)
σ(x,x).
2.从方差/协方差到协方差矩阵
根据方差的定义,给定
d
d
d个随机变量
x
k
,
k
=
1
,
2
,
.
.
.
d
x_k,k=1,2,...d
xk,k=1,2,...d,则这些随机变量的方差为 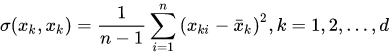 其中,为方便书写,
x
k
i
x_ki
xki表示随机变量
x
k
x_k
xk 中的第
i
i
i 个观测样本,
n
n
n 表示样本量,每个随机变量所对应的观测样本数量均为
n
n
n。 对于这些随机变量,我们还可以根据协方差的定义,求出两两之间的协方差,即 其中,为方便书写,
x
k
i
x_ki
xki表示随机变量
x
k
x_k
xk 中的第
i
i
i 个观测样本,
n
n
n 表示样本量,每个随机变量所对应的观测样本数量均为
n
n
n。 对于这些随机变量,我们还可以根据协方差的定义,求出两两之间的协方差,即 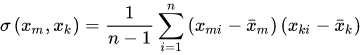 因此,协方差矩阵为 因此,协方差矩阵为 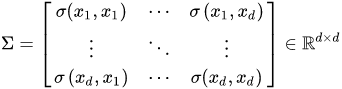 其中,对角线上的元素为各个随机变量的方差,非对角线上的元素为两两随机变量之间的协方差,根据协方差的定义,我们可以认定:矩阵
∑
\sum
∑为对称矩阵(symmetric matrix),其大小为
x
×
x
x\times x
x×x。 其中,对角线上的元素为各个随机变量的方差,非对角线上的元素为两两随机变量之间的协方差,根据协方差的定义,我们可以认定:矩阵
∑
\sum
∑为对称矩阵(symmetric matrix),其大小为
x
×
x
x\times x
x×x。
3.多元正态分布与线性变换
假设一个向量
x
x
x 服从均值向量为
u
u
u 、协方差矩阵为
∑
\sum
∑ 的多元正态分布(multi-variate Gaussian distribution),则 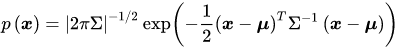 令该分布的均值向量为
u
=
0
u=0
u=0,由于指数项外面的系数
∣
2
π
∑
∣
−
1
/
2
|2\pi\sum|^{-1/2}
∣2π∑∣−1/2通常作为常数,故可将多元正态分布简化为 令该分布的均值向量为
u
=
0
u=0
u=0,由于指数项外面的系数
∣
2
π
∑
∣
−
1
/
2
|2\pi\sum|^{-1/2}
∣2π∑∣−1/2通常作为常数,故可将多元正态分布简化为 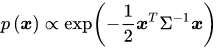 再令
x
=
(
y
,
z
)
T
x=(y,z)^T
x=(y,z)T ,包含两个随机变量
y
y
y和
z
z
z ,则协方差矩阵可写成如下形式: 再令
x
=
(
y
,
z
)
T
x=(y,z)^T
x=(y,z)T ,包含两个随机变量
y
y
y和
z
z
z ,则协方差矩阵可写成如下形式:
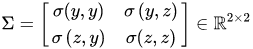
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = (12, 8)
# Normal distributed x and y vector with mean 0 and standard deviation 1
x = np.random.normal(0, 1, 500)
y = np.random.normal(0, 1, 500)
X = np.vstack((x, y)).T
plt.scatter(X[:, 0], X[:, 1])
plt.title('Generated Data')
plt.axis('equal');
用单位矩阵(identity matrix)
I
I
I 作为协方差矩阵,随机变量
y
y
y 和
z
z
z的方差均为1,则生成若干个随机数如图1所示  在生成的若干个随机数中,每个点的似然为 在生成的若干个随机数中,每个点的似然为 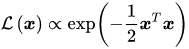 对图1中的所有点考虑一个线性变换(linear transformation):
t
=
A
x
t=Ax
t=Ax,我们能够得到图2. 对图1中的所有点考虑一个线性变换(linear transformation):
t
=
A
x
t=Ax
t=Ax,我们能够得到图2.  在线性变换中,矩阵 [公式] 被称为变换矩阵(transformation matrix),为了将图1中的点经过线性变换得到我们想要的图2,其实我们需要构造两个矩阵: 尺度矩阵(scaling matrix): 在线性变换中,矩阵 [公式] 被称为变换矩阵(transformation matrix),为了将图1中的点经过线性变换得到我们想要的图2,其实我们需要构造两个矩阵: 尺度矩阵(scaling matrix): 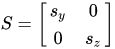 旋转矩阵(rotation matrix) 旋转矩阵(rotation matrix) 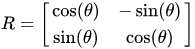 其中, [公式] 为顺时针旋转的度数。 其中, [公式] 为顺时针旋转的度数。
变换矩阵、尺度矩阵和旋转矩阵三者的关系式:
A
=
R
S
A=RS
A=RS
在这个例子中,尺度矩阵为 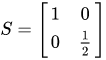 , 旋转矩阵为 , 旋转矩阵为 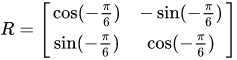 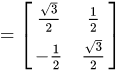 , 故变换矩阵为 , 故变换矩阵为 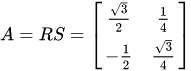
另外,需要考虑的是,经过了线性变换, [公式] 的分布是什么样子呢? 将
x
=
A
−
1
t
x=A^-1t
x=A−1t 带入前面给出的似然 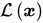 有 有 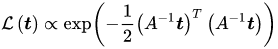 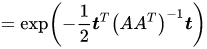 由此可以得到,多元正态分布的协方差矩阵为 由此可以得到,多元正态分布的协方差矩阵为 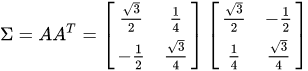 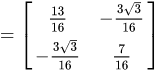
4.协方差矩阵的特征值分解
回到我们已经学过的线性代数内容,对于任意对称矩阵
∑
\sum
∑,存在一个特征值分解(eigenvalue decomposition, EVD):
∑
=
U
A
U
T
\sum=UAU^T
∑=UAUT 其中,
U
U
U的每一列都是相互正交的特征向量,且是单位向量,满足
U
T
U
=
I
U^TU=I
UTU=I ,
Λ
\Lambda
Λ对角线上的元素是从大到小排列的特征值,非对角线上的元素均为0。 当然,这条公式在这里也可以很容易地写成如下形式:
∑
=
(
U
Λ
1
/
2
)
(
U
Λ
1
/
2
)
T
=
A
A
T
\sum=(U\Lambda^{1/2})(U\Lambda^{1/2})^T=AA^T
∑=(UΛ1/2)(UΛ1/2)T=AAT 其中,
A
=
U
Λ
1
/
2
A=U\Lambda^{1/2}
A=UΛ1/2,因此,通俗地说,任意一个协方差矩阵都可以视为线性变换的结果。 在上面的例子中,特征向量构成的矩阵为 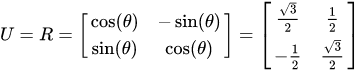 特征值构成的矩阵为 特征值构成的矩阵为 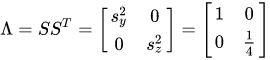 到这里,我们发现:多元正态分布的概率密度是由协方差矩阵的特征向量控制旋转(rotation),特征值控制尺度(scale),除了协方差矩阵,均值向量会控制概率密度的位置,在图1和图2中,均值向量为 [公式] ,因此,概率密度的中心位于坐标原点。 到这里,我们发现:多元正态分布的概率密度是由协方差矩阵的特征向量控制旋转(rotation),特征值控制尺度(scale),除了协方差矩阵,均值向量会控制概率密度的位置,在图1和图2中,均值向量为 [公式] ,因此,概率密度的中心位于坐标原点。
参考:Understanding the Covariance MatrixWhat is the Covariance Matrix?
| 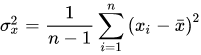 其中,
n
n
n 表示样本量,符号
x
‾
\overline x
x 表示观测样本的均值,这个定义在初中阶段就已经开始接触了。 在此基础上,协方差的计算公式被定义为
其中,
n
n
n 表示样本量,符号
x
‾
\overline x
x 表示观测样本的均值,这个定义在初中阶段就已经开始接触了。 在此基础上,协方差的计算公式被定义为 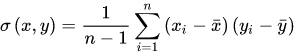 在公式中,符号
x
‾
\overline x
x,
y
‾
\overline y
y 分别表示两个随机变量所对应的观测样本均值,据此,我们发现:方差
σ
x
2
\sigma_x^2
σx2可视作随机变量
x
x
x关于其自身的协方差
σ
(
x
,
x
)
\sigma(x,x)
σ(x,x).
在公式中,符号
x
‾
\overline x
x,
y
‾
\overline y
y 分别表示两个随机变量所对应的观测样本均值,据此,我们发现:方差
σ
x
2
\sigma_x^2
σx2可视作随机变量
x
x
x关于其自身的协方差
σ
(
x
,
x
)
\sigma(x,x)
σ(x,x).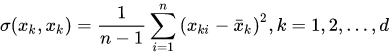 其中,为方便书写,
x
k
i
x_ki
xki表示随机变量
x
k
x_k
xk 中的第
i
i
i 个观测样本,
n
n
n 表示样本量,每个随机变量所对应的观测样本数量均为
n
n
n。 对于这些随机变量,我们还可以根据协方差的定义,求出两两之间的协方差,即
其中,为方便书写,
x
k
i
x_ki
xki表示随机变量
x
k
x_k
xk 中的第
i
i
i 个观测样本,
n
n
n 表示样本量,每个随机变量所对应的观测样本数量均为
n
n
n。 对于这些随机变量,我们还可以根据协方差的定义,求出两两之间的协方差,即 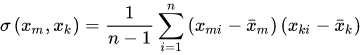 因此,协方差矩阵为
因此,协方差矩阵为 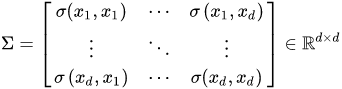 其中,对角线上的元素为各个随机变量的方差,非对角线上的元素为两两随机变量之间的协方差,根据协方差的定义,我们可以认定:矩阵
∑
\sum
∑为对称矩阵(symmetric matrix),其大小为
x
×
x
x\times x
x×x。
其中,对角线上的元素为各个随机变量的方差,非对角线上的元素为两两随机变量之间的协方差,根据协方差的定义,我们可以认定:矩阵
∑
\sum
∑为对称矩阵(symmetric matrix),其大小为
x
×
x
x\times x
x×x。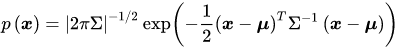 令该分布的均值向量为
u
=
0
u=0
u=0,由于指数项外面的系数
∣
2
π
∑
∣
−
1
/
2
|2\pi\sum|^{-1/2}
∣2π∑∣−1/2通常作为常数,故可将多元正态分布简化为
令该分布的均值向量为
u
=
0
u=0
u=0,由于指数项外面的系数
∣
2
π
∑
∣
−
1
/
2
|2\pi\sum|^{-1/2}
∣2π∑∣−1/2通常作为常数,故可将多元正态分布简化为 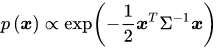 再令
x
=
(
y
,
z
)
T
x=(y,z)^T
x=(y,z)T ,包含两个随机变量
y
y
y和
z
z
z ,则协方差矩阵可写成如下形式:
再令
x
=
(
y
,
z
)
T
x=(y,z)^T
x=(y,z)T ,包含两个随机变量
y
y
y和
z
z
z ,则协方差矩阵可写成如下形式: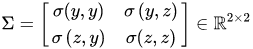
 在生成的若干个随机数中,每个点的似然为
在生成的若干个随机数中,每个点的似然为 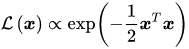 对图1中的所有点考虑一个线性变换(linear transformation):
t
=
A
x
t=Ax
t=Ax,我们能够得到图2.
对图1中的所有点考虑一个线性变换(linear transformation):
t
=
A
x
t=Ax
t=Ax,我们能够得到图2.  在线性变换中,矩阵 [公式] 被称为变换矩阵(transformation matrix),为了将图1中的点经过线性变换得到我们想要的图2,其实我们需要构造两个矩阵: 尺度矩阵(scaling matrix):
在线性变换中,矩阵 [公式] 被称为变换矩阵(transformation matrix),为了将图1中的点经过线性变换得到我们想要的图2,其实我们需要构造两个矩阵: 尺度矩阵(scaling matrix): 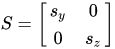 旋转矩阵(rotation matrix)
旋转矩阵(rotation matrix) 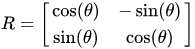 其中, [公式] 为顺时针旋转的度数。
其中, [公式] 为顺时针旋转的度数。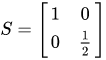 , 旋转矩阵为
, 旋转矩阵为 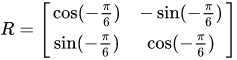
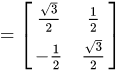 , 故变换矩阵为
, 故变换矩阵为 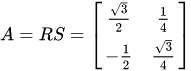
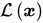 有
有 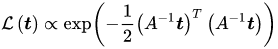
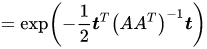 由此可以得到,多元正态分布的协方差矩阵为
由此可以得到,多元正态分布的协方差矩阵为 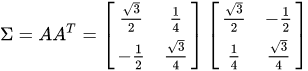
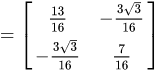
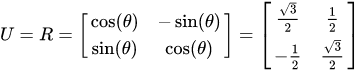 特征值构成的矩阵为
特征值构成的矩阵为 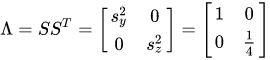 到这里,我们发现:多元正态分布的概率密度是由协方差矩阵的特征向量控制旋转(rotation),特征值控制尺度(scale),除了协方差矩阵,均值向量会控制概率密度的位置,在图1和图2中,均值向量为 [公式] ,因此,概率密度的中心位于坐标原点。
到这里,我们发现:多元正态分布的概率密度是由协方差矩阵的特征向量控制旋转(rotation),特征值控制尺度(scale),除了协方差矩阵,均值向量会控制概率密度的位置,在图1和图2中,均值向量为 [公式] ,因此,概率密度的中心位于坐标原点。