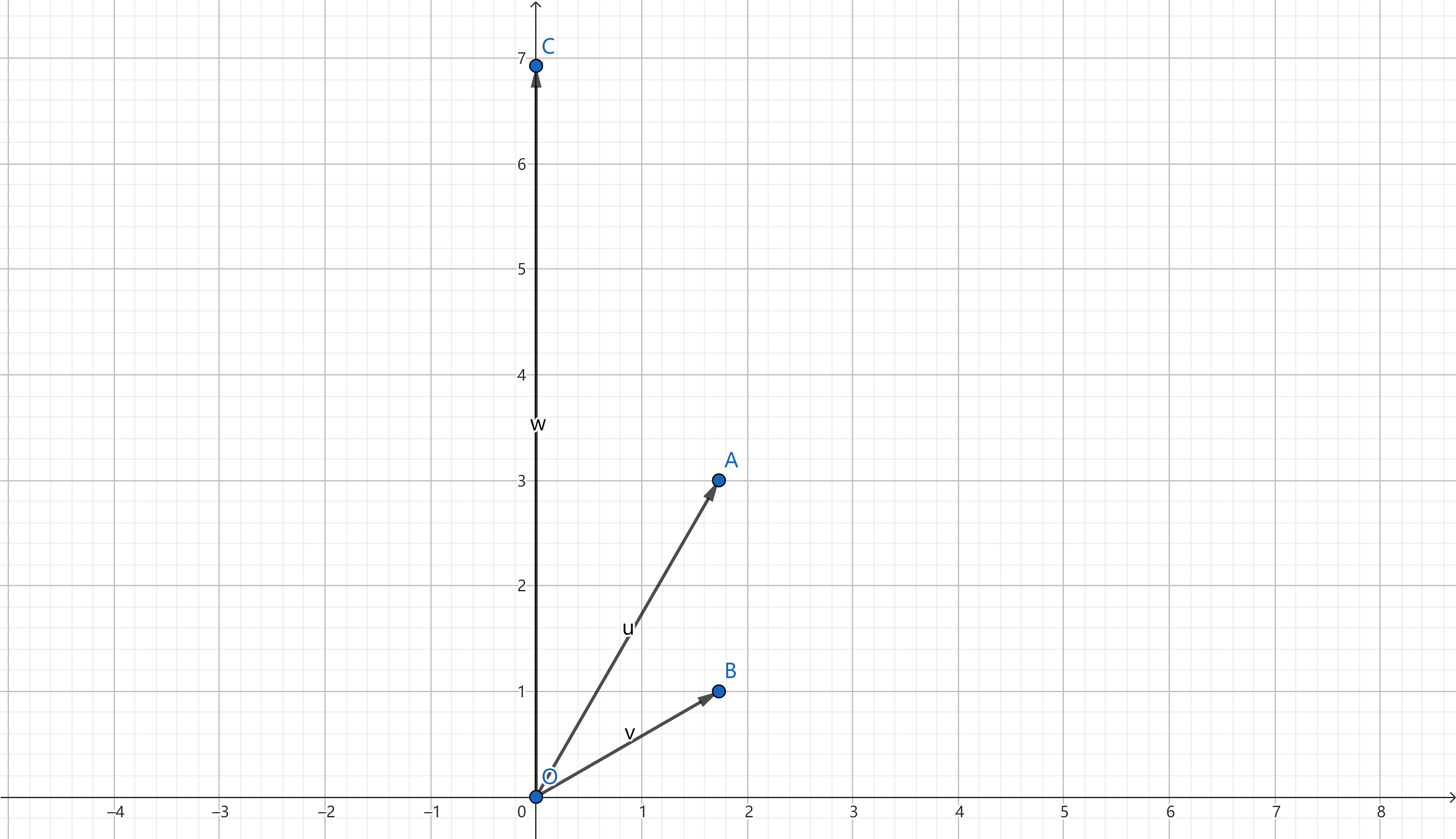
本文作者为 JustinRochester。

目录地址

上一篇

下一篇

我们考虑一个递推方程：\(f_n= \begin{cases} \begin{aligned} 2f_{n-1}-2f_{n-2}&,n\geq 2\\ n&,n\in\{0, 1\}\\ \end{aligned} \end{cases}\) 。我们可以递推出这个方程的前几项：

同时，我们可以通过特征方程法求出通项公式：\(\displaystyle f_n={(1+\sqrt{-1})^n-(1-\sqrt{-1})^n\over 2\sqrt{-1}}\)

很可惜，方程中涉及到了 \(\sqrt{-1}\) ，它在实数上是无解的。然而，假设我们将 \(\sqrt{-1}\) 当成一个单独的变元，计算后再通过 \((\sqrt{-1})^2=-1\) 可以重新得到上述的递推结果。例如：

\(\begin{aligned} f_5&={(1+\sqrt{-1})^5-(1-\sqrt{-1})^5\over 2\sqrt{-1}}\\ &={[1+5\sqrt{-1}+10(\sqrt{-1})^2+10(\sqrt{-1})^3+5({\sqrt{-1}})^4+({\sqrt{-1}})^5]-[1-5\sqrt{-1}+10(\sqrt{-1})^2-10(\sqrt{-1})^3+5({\sqrt{-1}})^4-({\sqrt{-1}})^5]\over 2\sqrt {-1}}\\ &={2[5\sqrt{-1}+10({\sqrt{-1}})^3+({\sqrt{-1}})^5]\over 2\sqrt{-1}}\\ &=5+10(\sqrt{-1})^2+(\sqrt{-1})^4 \end{aligned}\)

我们代入 \((\sqrt{-1})^2=-1\) 得到： \(f_5=5+10\cdot (-1)+(-1)^2=-4\) ，这和我们递推得到的结果一致。

这启示我们，\(\sqrt{-1}\) 是一个具有数学意义的单位。我们将其记为 \(i=\sqrt{-1}\) ，并命名为虚数，方便我们进一步研究它的性质。

我们称，形如 \(z=a+bi(a,b\in R, i=\sqrt{-1}, \text{ 下同})\) 的数字为虚数，其中必须满足 \(b\neq 0\) ，否则式子将退化为实数。

我们统称虚数（imaginary number）和实数（real number）为复数（complex number），因此复数的形式同上式一致，但不必满足 \(b\neq 0\) 条件。我们记复数集为字母 \(C\) 。

对于复数 \(z=a+bi\)，我们称 \(a\) 为它的实部，记为 \(\Re z=a\) 或 \(\text{Re }a\)；同理，称 \(b\) 为它的虚部，记为 \(\Im z=b\) 或 \(\text{Im }b\)。

我们称实部相同，虚部互为相反数的两个复数互为共轭复数。对于复数 \(z=a+bi\) ，我们记它的共轭复数 \(\bar z=a-bi\) 。

于是，根据定义，我们可以很快定义两个复数的加减乘三个运算：

\(z_1=a_1+b_1i,z_2=a_2+b_2i\)

则 \(z_1\pm z_2=(a_1\pm a_2)+(b_1\pm b_2)i\)

而 \(z_1\cdot z_2=a_1a_2+(a_1b_2+a_2b_1)i+b_1b_2i^2=a_1a_2+(a_1b_2+a_2b_1)i-b_1b_2=(a_1a_2-b_1b_2)+(a_1b_2+a_2b_1)i\)

对于除法，我们想直接写成上述的形式则比较困难了。有什么办法解决呢？

首先，我们观察一下，两个共轭复数的乘积会有什么特点：

\(z_2\cdot \bar{z_2}=(a_2a_2+b_2b_2)+(-a_2b_2+a_2b_2)i=a_2^2+b_2^2\in R\)

因此，当我们计算 \({z_1\over z_2}\) 时，我们往往会分子分母同乘一个 \(\bar z_2\) 使得分母实数化。如若需要展开来写，则是：

\(\displaystyle {z_1\over z_2}={z_1\cdot \bar{z_2}\over z_2\cdot \bar{z_2}}={(a_1a_2+b_1b_2)+(-a_1b_2+a_2b_1)i\over a_2^2+b_2^2}={a_1a_2+b_1b_2\over a_2^2+b_2^2}+{-a_1b_2+a_2b_1\over a_2^2+b_2^2}i\)

我们可以发现，复数在加减乘除的运算下，得到的答案仍然是复数；即复数和实数一样，在四则运算下是封闭的。

但是这仍然有个问题：实数在开方运算下不封闭，例如 \(-1\) 开平方运算后得到了 \(\sqrt{-1}=i\not\in R\) ，复数能满足这个要求吗？

若 \(\sqrt{i}\not\in C\) ，我们还需要定义“复复数”、“复复复数”、......这样的递归定义将显得非常鸡肋。

我们观察到，复数的加减法运算和二维直角坐标系上的向量的加减法运算形式一致。这启示我们，会不会复数的四则运算和二维直角坐标系上的一些几何性质相关。

显然，当复数进行加减法时，若 \(z_1=a_1+b_1i,z_2=a_2+b_2i\) 则 \(z_1\pm z_2=(a_1\pm a_2)+(b_1\pm b_2)i\) ；它等价于向量 \(\boldsymbol v_1=(a_1,b_1)^T\) 与向量 \(\boldsymbol v_2=(a_2,b_2)^T\) 进行加减法 \(\boldsymbol v_1\pm \boldsymbol v_2=(a_1\pm a_2, b_1\pm b_2)^T\) 。

但很可惜，二维向量并没有定义从两个二维向量到一个二维向量的乘法运算。因此，我们需要重新观察复数乘法的几何性质。

我们取两个复数 \(z_1=\sqrt 3+3 i, z_2=\sqrt 3+i\) ，两个向量的复数为 \(z=z_1\cdot z_2=4\sqrt 3i\) 。

这时候，我们如果在二维直角坐标系上画出三个向量，进行观察，会发现两个特殊的性质：

第一个向量的一个幅角（即从 \(x\) 正半轴逆时针旋转到向量的角度）为 \({\pi\over 3}\) ，第二个为 \({\pi\over 6}\) ，第三个为 \({\pi\over 2}\) 。而 \({\pi\over 2}={\pi\over 3}+{\pi\over 6}\) 。

此外，第一个向量的模长（即从原点到向量端点的长度）为 \(2\sqrt{3}\) ，第二个为 \(2\) ，第三个为 \(4\sqrt {3}\) 。而 \(4\sqrt{3}=2\sqrt{3}\cdot 2\) 。

似乎两个复数的乘积满足幅角相加和模长相乘两个性质。这是否是真的呢？

为了证明这个性质，首先我们对于向量 \(z=a+bi\) ，定义其模长 \(|z|=\sqrt{a^2+b^2}\) ，定义其幅角 \(\arg(z)=2k\pi+\text{Arg}(z)= \begin{cases} \begin{aligned} 2\arctan{b\over \sqrt{a^2+b^2}+a}&,b\neq 0\\ 0&,b=0\wedge a>0\\ \pi&,b=0\wedge a> (istream& in, vir &v) { return in>>v.r>>v.i; } inline friend ostream& operator >a>>b>>c>>d; cout