本文稍微有一点长，不过耐心读下去一定会有所收获的！

可以参考（电子版下载）

【圆锥曲线】第三定义以及斜率之积为定值模型

\color{green}{注意：}

以下内容均以焦点在 x 轴的椭圆和双曲线为研究对象，对于焦点在 y 轴上的椭圆和双曲线，以下所有结论的等号右边变更为 \color{red}{\frac{1}{e^2-1}}

理解∶ 在结论推导过程中，焦点在 x 轴与焦点在 y 轴上的唯一变化的是 x ， y 两个符号位置互换。

\color{red}{内容：} 平面内的动点到两定点 A_1(a_1，0) 、 A_2(a_2，0) （或A_1(0,a_1) A_2(0,a_2)）的斜率乘积等于常数 e²-1 的点的轨迹叫做椭圆或双曲线，其中两定点分别为椭圆或双曲线的顶点；

当常数大于 -1 小于 0 时为椭圆，当常数大于 0 时为双曲线。

由第三定义知∶ A 、 B 为椭圆或双曲线的顶点， P 是椭圆上异于 A 、 B 的一点，若 k_{PA} 、 k_{PB} 存在，

则有∶ \color{red}{k_{PA}\cdot k_{PB}=e^2-1} .

\color{red}{证明:}

（以椭圆∶ \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ( a>b>0 )为例）

如图，在椭圆∶\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ( a>b>0 ) 中， A(-a，0) 、 B(a，0) 是椭圆的左右顶点， P(x_0,y_0) 是椭圆上异于 A 、 B 的一点，

因为A(-a，0)、 P(x_0,y_0) 在椭圆上，

所以 \left\{ \begin {array}{rcl}\frac{a^2}{a^2}+\frac{0^2}{b^2}=1…\color{blue}{(1)}\\ \frac{x_0^2}{a^2}+\frac{y_0^2}{b^2}=1…\color{blue}{(2)}\end {array}\right.\ \ ，

\color{blue}{(1)}-\color{blue}{(2)} 得： \frac{(x_0+a)(x_0-a)}{a^2}+\frac{y_0^2}{b^2}=0 ，

即 \frac{y_0^2}{(x_0+a)(x_0-a)} =-\frac{b^2}{a^2} =e^2-1 …… \color{blue}{(3)}

取 AP 中点 M(\frac{x_0+(-a)}{2},\frac{y_0}{2}) ，连接 OM ，则 OM//PB ，

于是 k_{PA}\cdot k_{PB} =k_{PA}\cdot k_{OM} =\frac{y_0}{x_0-(-a)}\cdot\frac{\frac{y_0}{2}}{\frac{x_0-a}{2}} .

由\color{blue}{(3)}知，\color{red}{k_{PA}\cdot k_{PB}}=k_{PA}\cdot k_{OM} =\frac{y_0}{x_0+a}\cdot\frac{y_0}{x_0-a}=\color{red}{e^2-1} .

通过上述证明过程，不难发现，只要 A 、 B 两点关于原点对称，上述证明过程即成立，于是我们有如下推广∶

A 、 B 为椭圆或双曲线上关于原点对称的两点， P 是椭圆上异于 A、 B的一点，若k_{PA} 、 k_{PB}存在，

则有∶ \color{red}{k_{PA}\cdot k_{PB}=e^2-1} .

\color{red}{证明:}

（以椭圆∶ \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ( a>b>0 )为例）

如图，在椭圆∶\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ( a>b>0 )中， A(x_1，y_1) 、 B(x_2，y_2) 是椭圆的关于原点对称的两点， P(x_0,y_0) 是椭圆上异于 A 、 B 的一点，

因为A(x_1，y_1)、 P(x_0,y_0) 在椭圆上，所以∶ \left\{ \begin {array}{rcl}\frac{x_1^2}{a^2}+\frac{y_1^2}{b^2}=1…\color{blue}{(1)}\\ \frac{x_0^2}{a^2}+\frac{y_0^2}{b^2}=1…\color{blue}{(2)}\end {array}\right.\ \ ，

\color{blue}{(1)}-\color{blue}{(2)} 得： \frac{(x_0+x_1)(x_0-x_1)}{a^2}+\frac{(y_0+y_1)(y_0-y_1)}{b^2}=0 即 \frac{(y_0+y_1)(y_0-y_1)}{(x_0+x_1)(x_0-x_1)} =-\frac{b^2}{a^2} =e^2-1 …… \color{blue}{(3)}

取 AP 中点 M(\frac{x_0+x_1}{2},\frac{y_0+y_1}{2}) ，连接 OM ，则 OM//PB ，

于是 k_{PA}\cdot k_{PB} =k_{PA}\cdot k_{OM} =\frac{y_0-y_1}{x_0-x_1}\cdot\frac{\frac{y_0+y_1}{2}}{\frac{x_0+x_1}{2}} .

由\color{blue}{(3)}知，\color{red}{k_{PA}\cdot k_{PB}}=k_{PA}\cdot k_{OM} =\frac{y_0-y_1}{x_0-x_1}\cdot\frac{y_0+y_1}{x_0+x_1} =\color{red}{e^2-1} .

A 、 B 为椭圆或双曲线上关于原点对称的两点， P 是椭圆上异于A 、 B 的一点，若k_{PA} 、 k_{PB}存在，

则有∶ \color{red}{k_{PA}\cdot k_{PB}=e^2-1} .

细心的朋友能够发现，一次推广和二次推广的证明过程都得到了一个附加结论\color{red}{k_{PA}\cdot k_{OM}=e^2-1} ，

由此我们进行第三次推广∶

A 、 B 为椭圆或双曲线上任意两点， M 是 AB 的中点，则有∶\color{red}{k_{AB}\cdot k_{OM}=e^2-1} .

\color{red}{证明:} \color{blue}{（点差法）}

（以椭圆∶ \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ( a>b>0 )为例）

如图，在椭圆∶ \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ( a>b>0 )中， A(x_1，y_1) 、 B(x_2，y_2) 是椭圆上任意两点，

因为A(x_1，y_1)、B(x_2，y_2) 在椭圆上，

所以∶ \left\{ \begin {array}{rcl}\frac{x_1^2}{a^2}+\frac{y_1^2}{b^2}=1…\color{blue}{(1)}\\ \frac{x_2^2}{a^2}+\frac{y_2^2}{b^2}=1…\color{blue}{(2)}\end {array}\right.\ \ ，

\color{blue}{(1)}-\color{blue}{(2)} 得： \frac{(x_1+x_2)(x_1-x_2)}{a^2}+\frac{(y_1+y_2)(y_1-y_2)}{b^2}=0

即 \frac{(y_1+y_2)(y_1-y_2)}{(x_1+x_2)(x_1-x_2)} =-\frac{b^2}{a^2} =e^2-1 …… \color{blue}{(3)}

取 AB 中点 M(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}) ，连接 OM ，

于是 \color{red}{k_{AB}\cdot k_{OM}} =\frac{y_1-y_2}{x_1-x_2}\cdot\frac{\frac{y_1+y_2}{2}}{\frac{x_1+x_2}{2}} =\color{red}{e^2-1} .

在此再补充一个结果是 \color{red}{e^2-1} 的结论，方便读者朋友记忆∶直线 AB 与椭圆相切于点 M ，连接 OM ，则有∶ \color{red}{k_{AB}\cdot k_{OM}=e^2-1} .

结论的证明可以结合仿射变化相关内容进行证明，也可以运用A 、 B 两点无限趋近为一点时的点差法理解，如图。

\color{blue }{综上所述：} 我们有如下七种斜率乘积为 \color{red}{e^2-1} 的模型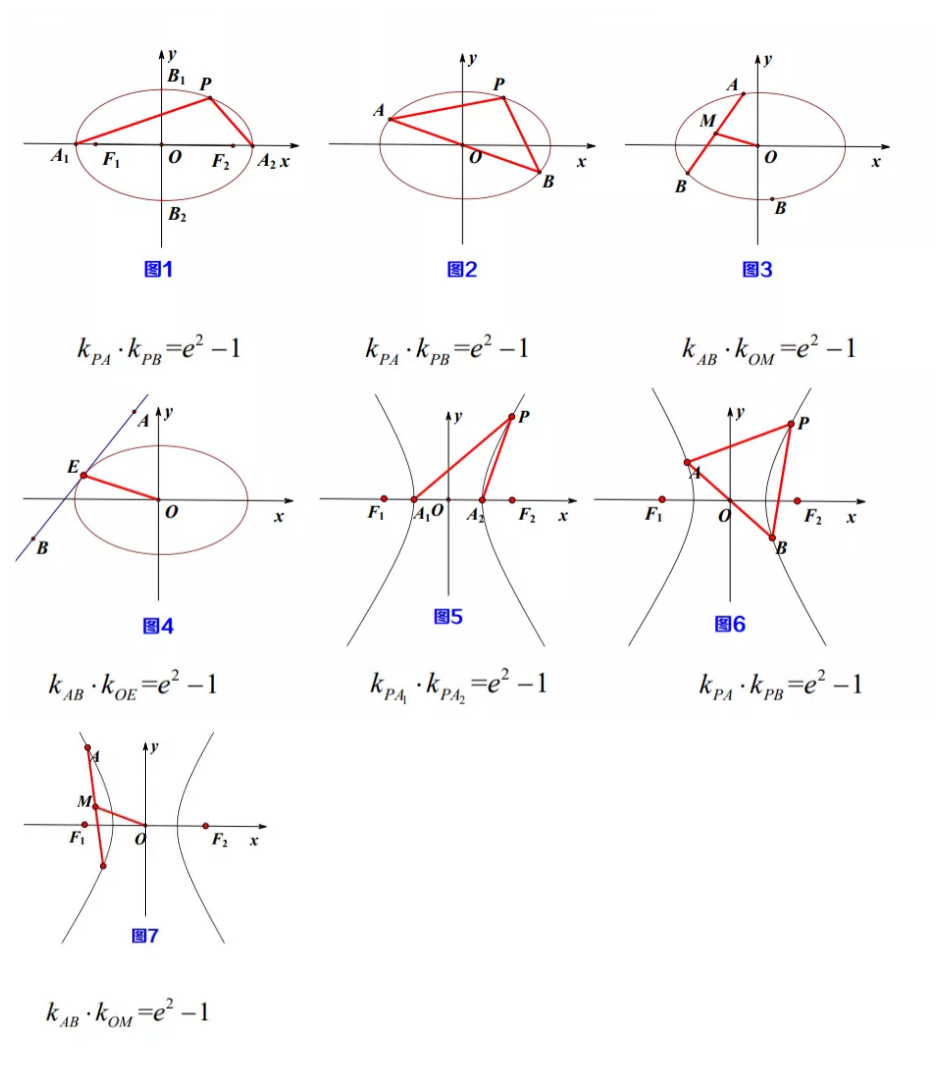

\color{green}{例1. } P 是双曲线∶\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 ( a>0 b>0 ) 上一点， M ， N 分别是双曲线的左右顶点，直线 PM ， PN 的斜率之积为 \frac{1}{5} ，则双曲线离心率为_______.

\color{purple}{解析∶}

由第三定义知，k_{PM}\cdot k_{PN}=e^2-1 =\frac{1}{5} 解得： e=\frac{\sqrt{30}}{5} .

\color{green}{例2.} 已知双曲线 C ∶ x²-y²=2020 的左右顶点分别为 A 、 B ， P 为双曲线右支一点，且 \angle{PAB}=4\angle{APB} ，求 \angle{APB}= _______.

\color{purple}{解析∶}

令 \angle{APB}=\alpha ，由题意得 \alpha\in(0,\frac{\pi}{4}) ，外角 \angle{PBx}=\angle{APB}+\angle{PAB} ， \angle{PBx}=5\alpha ，则由双曲线的第三定义知∶k_{PA}\cdot k_{PB}=e^2-1 =\tan4α\cdot\tan5α =1 则 \tan4α=\frac{1}{\tan5α} =\tan (\frac{\pi}{2}-5\alpha) ，

所以 4\alpha=\frac{\pi}{2}-5\alpha ，即 \alpha=\frac{\pi}{18} .

\color{green}{例3.} 已知 A 、 B 是椭圆\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ( a>b>0 )长轴的两个端点， M 、 N 是椭圆上关于 x 轴对称的两点，直线 AM 、 BN 的斜率分别为 k_1 、 k_2 ，且 k_1k_2≠0 若 \left| k_1 \right|+\left| k_2 \right| 的最小值为 1 ，则椭圆的离心率为____.

\color{purple}{解析∶}

由题意可作图如下∶

连接 MB ，由椭圆的第三定义可知∶k_{AM}\cdot k_{BM}=e^2-1 =-\frac{b^2}{a^2} ，

而 k_{BM}=-k_{BN} ，所以 k_1k_2 =\frac{b^2}{a^2} ，

\left| k_1 \right|+\left| k_2 \right| \geq 2\sqrt{ \left| k_1 \right|\cdot\left| k_2 \right| } =\frac{2b}{a} =1 ，

因此 e=\frac{\sqrt{3}}{2} .

\color{green}{例 4.} 已知 A 、 B 是椭圆\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ( a>b>0 )长轴的两个端点，若椭圆上存在点 Q ，使 \angle{AQB}=\frac{2\pi}{3} ，则椭圆的离心率的取值范围为_____.

\color{purple}{解析∶}

令 Q 在 x 轴上方，则直线 QA 的倾斜角为 \alpha\in(0,\frac{\pi}{3}) ，直线 QB 的倾斜角为 \beta=\alpha+\frac{2\pi}{3} \in(\frac{2\pi}{3},\pi) .

由椭圆的第三定义∶ \tanα\cdot\tanβ =\tanα\cdot\tan(\alpha+\frac{2\pi}{3}) =e^2-1

即 \tanα\cdot\frac{\tanα-\sqrt{3}}{1+\sqrt{3}\tan\alpha} =e^2-1 ，

令 1+\sqrt{3}\tan\alpha=t \in(1,4) ，

则 e^2-1 =\frac{t}{3}+\frac{4}{3t}-\frac{5}{3} \geq-\frac{1}{3}

所以 e^2≥\frac{2}{3} ，即 e\geq\frac{\sqrt{6}}{3} ，当 t=2 时等号成立，故 e\in[\frac{\sqrt{6}}{3},1) .