张量的概念及基本运算 |
您所在的位置:网站首页 › 内积的表达式 › 张量的概念及基本运算 |
张量的概念及基本运算
|
张量的概念及基本运算
文章目录
张量的概念及基本运算1 张量的定义2 纤维(Fibers)与 切片(Slices)2.1 纤维(Fibers)2.2 切片(Slices)
3 张量的范数(norm)4 张量的内积(inner product)5 秩1张量(Rank-One Tensors)6 对称性与张量(Symmetry and Tensors)6.1 立方张量(cubical tensors)6.2 超对称张量(super symmetric)6.3 部分对称张量(partically symmetric)
7 对角张量(Diagonal Tensors)8 矩阵化:将张量转化为矩阵(Matricization: Transforming a Tensor into a Matrix)9 张量乘积:n模乘(Tensor Multiplication : The n-Mode Product)9.1 n模矩阵积(n-mode matrix product)9.2 n模向量积(The n-mode vector product)
10 矩阵Kronecker积、Khatri–Rao积与Hadamard积10.1 Kronecker积10.2 Khatri–Rao积10.3 Hadamard积10.4 性质
1 张量的定义
张量是一个多维数组。更正式地说,一个 N 阶张量是 N 个向量空间元素的张量积,每个向量空间都有自己的坐标系。 张量的阶数(the order of a tensor)也称为维数(dimensions)、模态(modes)、或方式(ways)。 一阶张量是一个矢量,二阶张量是一个矩阵,三阶或更高阶的张量叫做高阶张量。  2 纤维(Fibers)与 切片(Slices)
2.1 纤维(Fibers)
2 纤维(Fibers)与 切片(Slices)
2.1 纤维(Fibers)
纤维(Fibers) 是矩阵的行和列的高阶类似物。(纤维是指从张量中抽取的向量) 例如,矩阵 A 的列为mode-1纤维,行为mode-2纤维; 三阶张量有 列(column) 、行(row) 、管(tube) 纤维,分别用 x : , j , k {{\bf{x}}_{:,j,k}} x:,j,k , x i , : , k {{\bf{x}}_{i,:,k}} xi,:,k , x i , j , : {{\bf{x}}_{i,j,:}} xi,j,: 表示。 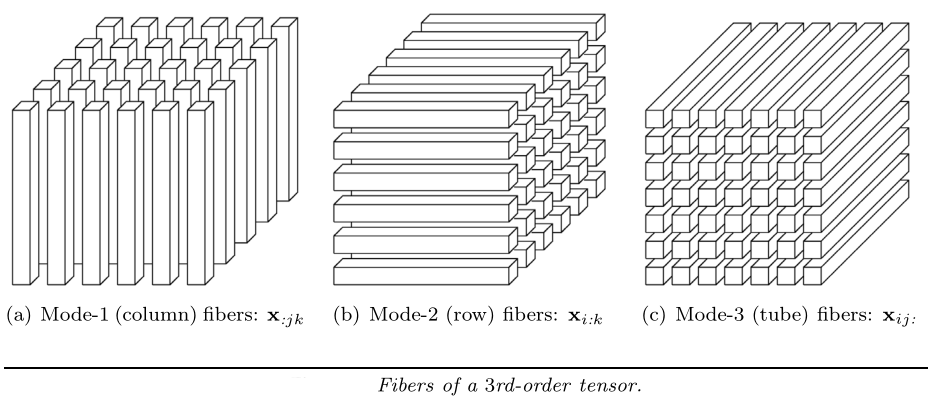 2.2 切片(Slices)
2.2 切片(Slices)
切片 (Slices) 是一个张量的二维切片,通过固定除两个维度之外的索引来定义。(切片是指从张量中抽取的矩阵) 例如,三阶张量 X \mathscr{X} X 的 水平面(horizontal) 、 侧面(lateral) 和 正面(frontal) 的切片,分别用 X i , : , : {\bf{X}}_{i,:,:} Xi,:,: , X : , j , : {\bf{X}}_{:,j,:} X:,j,: 和 X : , : , k {\bf{X}}_{:,:,k} X:,:,k 表示,且 X : , : , k {\bf{X}}_{:,:,k} X:,:,k 可简记为 X k {\bf{X}}_{k} Xk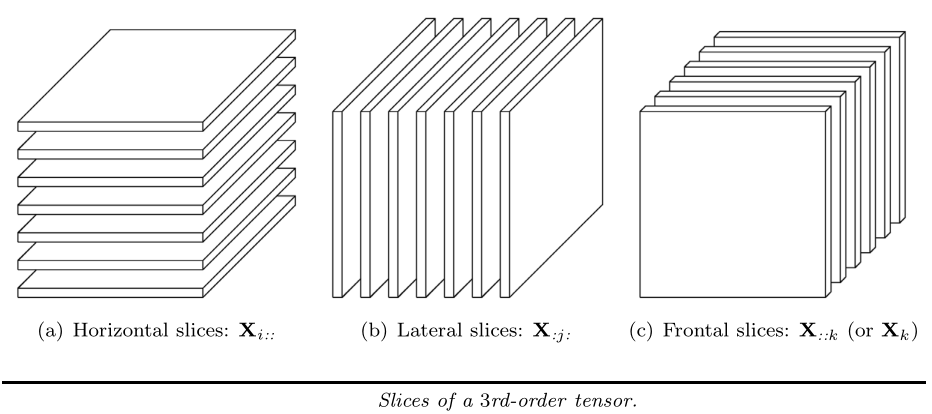 3 张量的范数(norm)
3 张量的范数(norm)
张量 X ∈ R I 1 × I 2 × ⋯ × I N \mathscr{X} \in \mathbb{R}^{I_{1} \times I_{2} \times \cdots \times I_{N}} X∈RI1×I2×⋯×IN 的范数是其所有元素平方和的平方根,即: ∥ X ∥ = ∑ i 1 = 1 I 1 ∑ i 2 = 1 I 2 ⋯ ∑ i N = 1 I N x i 1 i 2 ⋯ i N 2 \|\mathscr{X}\|=\sqrt{\sum_{i_{1}=1}^{I_{1}} \sum_{i_{2}=1}^{I_{2}} \cdots \sum_{i_{N}=1}^{I_{N}} x_{i_{1} i_{2} \cdots i_{N}}^{2}} ∥X∥=i1=1∑I1i2=1∑I2⋯iN=1∑INxi1i2⋯iN2 这类似于矩阵 A \bf{A} A 的 F范数(Frobenius norm). 4 张量的内积(inner product)两个相同大小张量 X , Y ∈ R I 1 × I 2 × ⋯ × I N \mathscr{X}, \mathscr{Y} \in \mathbb{R}^{I_{1} \times I_{2} \times \cdots \times I_{N}} X,Y∈RI1×I2×⋯×IN 的内积,即 ⟨ X , Y ⟩ = ∑ i 1 = 1 I 1 ∑ i 2 = 1 I 2 ⋯ ∑ i N = 1 I N x i 1 i 2 ⋯ i N y i 1 i 2 ⋯ i N \langle \mathscr{X}, \mathscr{Y} \rangle=\sum_{i_{1}=1}^{I_{1}} \sum_{i_{2}=1}^{I_{2}} \cdots \sum_{i_{N}=1}^{I_{N}} x_{i_{1} i_{2} \cdots i_{N}} y_{i_{1} i_{2} \cdots i_{N}} ⟨X,Y⟩=i1=1∑I1i2=1∑I2⋯iN=1∑INxi1i2⋯iNyi1i2⋯iN 且有 ⟨ X , X ⟩ = ∥ X ∥ 2 \langle\mathscr{X}, \mathscr{X}\rangle=\|\mathscr{X}\|^{2} ⟨X,X⟩=∥X∥2 5 秩1张量(Rank-One Tensors)一个 N 维张量 X ∈ R I 1 × I 2 × ⋯ × I N \mathscr{X} \in \mathbb{R}^{I_{1} \times I_{2} \times \cdots \times I_{N}} X∈RI1×I2×⋯×IN ,如果可以被写成 N 个向量的张量外积(outer product) , X = a ( 1 ) ∘ a ( 2 ) ∘ ⋯ ∘ a ( N ) \mathscr{X}=\mathbf{a}^{(1)} \circ \mathbf{a}^{(2)} \circ \cdots \circ \mathbf{a}^{(N)} X=a(1)∘a(2)∘⋯∘a(N) 则这个张量的秩为1. 其中,符号“◦”代表张量外积,即,张量的每个元素都是对应的向量元素的乘积: x i 1 i 2 ⋯ i N = a i 1 ( 1 ) a i 2 ( 2 ) ⋯ a i N ( N ) for all 1 ≤ i n ≤ I n x_{i_{1} i_{2} \cdots i_{N}}=a_{i_{1}}^{(1)} a_{i_{2}}^{(2)} \cdots a_{i_{N}}^{(N)} \quad \text { for all } 1 \leq i_{n} \leq I_{n} xi1i2⋯iN=ai1(1)ai2(2)⋯aiN(N) for all 1≤in≤In 下图展示了 X = a ∘ b ∘ c \mathscr{X} =a \circ b \circ c X=a∘b∘c,一个三阶秩1张量  注: ① 张量外积(Outer Product) 是线性代数中的外积, 也就是张量积(Tensor Product);克罗内克积(Kronecker Product)是张量积在矩阵中的特殊形式。 ② 向量外积(Exterior Product) 是解析几何中的外积,也叫叉积(Cross Product)。
6 对称性与张量(Symmetry and Tensors)
6.1 立方张量(cubical tensors)
注: ① 张量外积(Outer Product) 是线性代数中的外积, 也就是张量积(Tensor Product);克罗内克积(Kronecker Product)是张量积在矩阵中的特殊形式。 ② 向量外积(Exterior Product) 是解析几何中的外积,也叫叉积(Cross Product)。
6 对称性与张量(Symmetry and Tensors)
6.1 立方张量(cubical tensors)
如果一个张量的每个维度大小相同, X ∈ R I × I × I × ⋯ × I \mathscr{X} \in \mathbb{R}^{I \times I \times I \times \cdots \times I} X∈RI×I×I×⋯×I,那么这个张量就叫做立方(cubical)张量; 6.2 超对称张量(super symmetric)如果立方张量在任何索引排列下都保持不变,则立方张量称为超对称张量(supersymmetric)(或对称张量)。 例如,如果满足以下条件,则三阶张量 X ∈ R I × I × I \mathscr{X} \in \mathbb{R}^{I \times I \times I} X∈RI×I×I 是超对称的 x i j k = x i k j = x j i k = x j k i = x k i j = x k j i for all i , j , k = 1 , … , I x_{i j k}=x_{i k j}=x_{j i k}=x_{j k i}=x_{k i j}=x_{k j i} \quad \text { for all } i, j, k=1, \ldots, I xijk=xikj=xjik=xjki=xkij=xkji for all i,j,k=1,…,I 6.3 部分对称张量(partically symmetric)张量也可在两个或多个维度下(部分)对称。 例如,对于三阶张量 X ∈ R I × I × K \mathscr{X} \in \mathbb{R}^{I \times I \times K} X∈RI×I×K ,如果所有的正面切片都是对称的, X k = X k ⊤ for all k = 1 , … , K \mathbf{X}_{k}=\mathbf{X}_{k}^{\top} \quad \text { for all } k=1, \ldots, K Xk=Xk⊤ for all k=1,…,K 则该三阶张量在mode-1 和 mode-2 下是对称的。 7 对角张量(Diagonal Tensors)如果一个张量 X ∈ R I 1 × I 2 × ⋯ × I N \mathscr{X} \in \mathbb{R}^{I_{1} \times I_{2} \times \cdots \times I_{N}} X∈RI1×I2×⋯×IN ,当且仅当 x i 1 i 2 ⋯ i N ≠ 0 x_{i_{1} i_{2} \cdots i_{N}} \neq 0 xi1i2⋯iN=0 时,有 i 1 = i 2 = ⋯ = i N i_{1}=i_{2}=\cdots=i_{N} i1=i2=⋯=iN ,则该张量是对角(diagonal)张量。 下图展示了一个沿超对角线分布的立方张量。 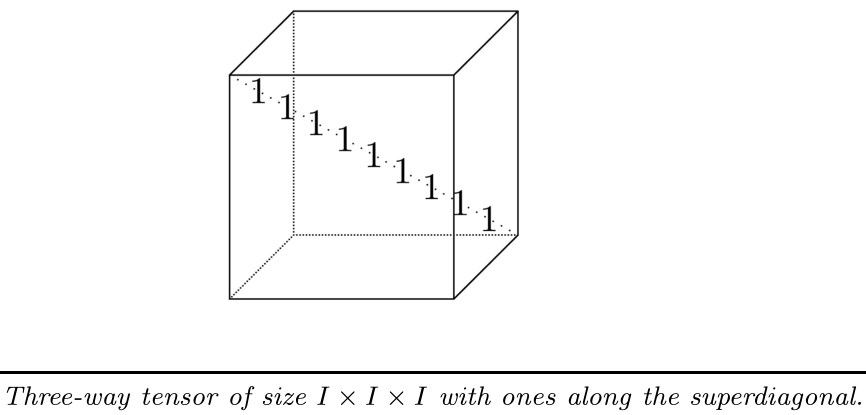 8 矩阵化:将张量转化为矩阵(Matricization: Transforming a Tensor into a Matrix)
8 矩阵化:将张量转化为矩阵(Matricization: Transforming a Tensor into a Matrix)
矩阵化(Matricization),也就是所谓的“展开”(unfolding)或“压扁”(flattening),是将一个 n 维数组中的元素重新排列成一个矩阵的过程。 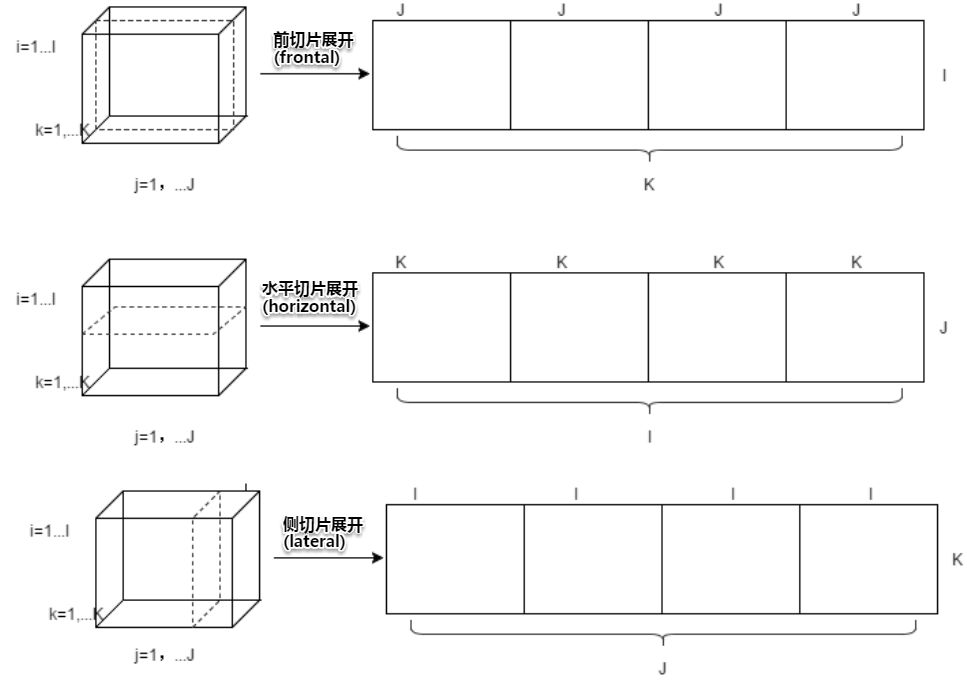 例如,一个2×3×4张量可以被重排成一个 6×4 或 3×8 的矩阵等。
例如,一个2×3×4张量可以被重排成一个 6×4 或 3×8 的矩阵等。
张量 X ∈ R I 1 × I 2 × ⋯ × I N \mathscr{X} \in \mathbb{R}^{I_{1} \times I_{2} \times \cdots \times I_{N}} X∈RI1×I2×⋯×IN 的 mod-n 矩阵化记为 X ( n ) \mathbf{X}_{(n)} X(n) ,它是将第 n 维纤维作为结果矩阵的列。即将张量元素 ( i 1 , i 2 , … , i N ) \left(i_{1}, i_{2}, \ldots, i_{N}\right) (i1,i2,…,iN) 映射到矩阵元素 ( i n , j ) \left(i_{n}, j\right) (in,j) 中 j = 1 + ∑ k = 1 k ≠ n N ( i k − 1 ) J k with J k = ∏ m = 1 m ≠ n k − 1 I m j=1+\sum_{k=1 \atop k \neq n}^{N}\left(i_{k}-1\right) J_{k} \quad \text { with } \quad J_{k}=\prod_{m=1 \atop m \neq n}^{k-1} I_{m} j=1+k=nk=1∑N(ik−1)Jk with Jk=m=nm=1∏k−1Im 例,设张量 x ∈ R 3 × 4 × 2 \mathscr{x} \in \mathbb{R}^{3 \times 4 \times 2} x∈R3×4×2 的前切片为: X 1 = [ 1 4 7 10 2 5 8 11 3 6 9 12 ] , X 2 = [ 13 16 19 22 14 17 20 23 15 18 21 24 ] \mathbf{X}_{1} = \left[\begin{array}{llll} 1 & 4 & 7 & 10 \\ 2 & 5 & 8 & 11 \\ 3 & 6 & 9 & 12 \end{array}\right] , \quad \mathbf{X}_{2} = \left[\begin{array}{llll} 13 & 16 & 19 & 22 \\ 14 & 17 & 20 & 23 \\ 15 & 18 & 21 & 24 \end{array}\right] X1=⎣⎡123456789101112⎦⎤,X2=⎣⎡131415161718192021222324⎦⎤则三个mode-n的展开分别是 X ( 1 ) = [ 1 4 7 10 13 16 19 22 2 5 8 11 14 17 20 23 3 6 9 12 15 18 21 24 ] X ( 2 ) = [ 1 2 3 13 14 15 4 5 6 16 17 18 7 8 9 19 20 21 10 11 12 22 23 24 ] X ( 3 ) = [ 1 2 3 4 5 ⋯ 9 10 11 12 13 14 15 16 17 ⋯ 21 22 23 24 ] \begin{aligned} \mathbf{X}_{(1)} &= \left[\begin{array}{llllllll} 1 & 4 & 7 & 10 & 13 & 16 & 19 & 22 \\ 2 & 5 & 8 & 11 & 14 & 17 & 20 & 23 \\ 3 & 6 & 9 & 12 & 15 & 18 & 21 & 24 \end{array}\right] \\ \mathbf{X}_{(2)}&=\left[\begin{array}{cccccc} 1 & 2 & 3 & 13 & 14 & 15 \\ 4 & 5 & 6 & 16 & 17 & 18 \\ 7 & 8 & 9 & 19 & 20 & 21 \\ 10 & 11 & 12 & 22 & 23 & 24 \end{array}\right] \\ \mathbf{X}_{(3)}&=\left[\begin{array}{cccccccccc} 1 & 2 & 3 & 4 & 5 & \cdots & 9 & 10 & 11 & 12 \\ 13 & 14 & 15 & 16 & 17 & \cdots & 21 & 22 & 23 & 24 \end{array}\right] \end{aligned} X(1)X(2)X(3)=⎣⎡123456789101112131415161718192021222324⎦⎤=⎣⎢⎢⎡147102581136912131619221417202315182124⎦⎥⎥⎤=[113214315416517⋯⋯921102211231224] 最后,向量化一个张量也是可以。同样,只要元素的顺序是一致的,它就不重要。在上面的例子中,向量化的版本是: vec ( X ) = [ 1 2 ⋮ 24 ] \operatorname{vec}(\boldsymbol{X})=\left[\begin{array}{c} 1 \\ 2 \\ \vdots \\ 24 \end{array}\right] vec(X)=⎣⎢⎢⎢⎡12⋮24⎦⎥⎥⎥⎤ 9 张量乘积:n模乘(Tensor Multiplication : The n-Mode Product)张量可以相乘,尽管显然它的符号和符号要比矩阵复杂得多。对于张量乘法的完整处理参见:Bader, MATLAB Tensor Classes forFast Algorithm Prototyping,2006. 这里我们只考虑张量n模乘(n-mode product),即用一个张量乘以一个n维矩阵(或向量)。 9.1 n模矩阵积(n-mode matrix product)(1)定义 张量 X ∈ R I 1 × I 2 × ⋯ × I N \mathscr{X} \in \mathbb{R}^{I_{1} \times I_{2} \times \cdots \times I_{N}} X∈RI1×I2×⋯×IN 与矩阵 U ∈ R J × I n \mathbf{U} \in\mathbb{R}^{J \times I_{n}} U∈RJ×In 的n模(矩阵)积记为 X × n U \mathscr{X} \times_{n} \mathbf{U} X×nU ,尺寸为 I 1 × ⋯ × I n − 1 × J × I n + 1 × ⋯ × I N I_{1} \times \cdots \times I_{n-1} \times J \times I_{n+1} \times \cdots \times I_{N} I1×⋯×In−1×J×In+1×⋯×IN 。从元素上看有: ( X × n U ) i 1 ⋯ i n − 1 j i n + 1 ⋯ i N = ∑ i n = 1 I n x i 1 i 2 ⋯ i N u j i n \left(\mathscr{X} \times_{n} \mathbf{U}\right)_{i_{1} \cdots i_{n-1} j i_{n+1} \cdots i_{N}}=\sum_{i_{n}=1}^{I_{n}} x_{i_{1} i_{2} \cdots i_{N}} u_{j i_{n}} (X×nU)i1⋯in−1jin+1⋯iN=in=1∑Inxi1i2⋯iNujin 即每个n模纤维都乘以矩阵 U \bf{U} U。这个想法也可以用矩阵化张量表示: Y = X × n U ⇔ Y ( n ) = U X ( n ) \mathscr{Y}=\mathscr{X} \times_{n} \mathbf{U} \quad \Leftrightarrow \quad \mathbf{Y}_{(n)}=\mathbf{U X}_{(n)} Y=X×nU⇔Y(n)=UX(n) (2)例题 设张量 x ∈ R 3 × 4 × 2 \mathscr{x} \in \mathbb{R}^{3 \times 4 \times 2} x∈R3×4×2 的前切片为: X 1 = [ 1 4 7 10 2 5 8 11 3 6 9 12 ] , X 2 = [ 13 16 19 22 14 17 20 23 15 18 21 24 ] \mathbf{X}_{1} = \left[\begin{array}{llll} 1 & 4 & 7 & 10 \\ 2 & 5 & 8 & 11 \\ 3 & 6 & 9 & 12 \end{array}\right] , \quad \mathbf{X}_{2} = \left[\begin{array}{llll} 13 & 16 & 19 & 22 \\ 14 & 17 & 20 & 23 \\ 15 & 18 & 21 & 24 \end{array}\right] X1=⎣⎡123456789101112⎦⎤,X2=⎣⎡131415161718192021222324⎦⎤ 矩阵: U = [ 1 3 5 2 4 6 ] \mathbf{U}=\begin{bmatrix}1&3&5\\2&4&6\end{bmatrix} U=[123456] 则张量与矩阵的1模乘为: Y = X × 1 U ∈ R 2 × 4 × 2 \mathscr{Y}=\mathscr{X}\times_{1}\mathbf{U}\in\mathbb{R}^{2\times4\times2} Y=X×1U∈R2×4×2 其中, Y 1 = [ 22 49 76 103 28 64 100 136 ] , Y 2 = [ 130 157 184 211 172 208 244 280 ] \mathbf{Y}_{1}=\left[\begin{array}{cccc} 22 & 49 & 76 & 103 \\ 28 & 64 & 100 & 136 \end{array}\right], \quad \mathbf{Y}_{2}=\left[\begin{array}{cccc} 130 & 157 & 184 & 211 \\ 172 & 208 & 244 & 280 \end{array}\right] Y1=[2228496476100103136],Y2=[130172157208184244211280] (3)基本运算法则 ① 连模乘 对于一系列乘法中的不同mode,乘法的顺序是不相关的,即 X × m A × n B = X × n B × m A ( m ≠ n ) \mathscr{X} \times_{m} \mathbf{A} \times_{n} \mathbf{B}=\mathscr{X} \times_{n} \mathbf{B} \times_{m} \mathbf{A} \quad(m \neq n) X×mA×nB=X×nB×mA(m=n) 如果mode相同,则 X × n A × n B = X × n ( B A ) \mathscr{X} \times_{n} \mathbf{A} \times_{n} \mathbf{B}=\mathscr{X} \times_{n} \left( \mathbf{BA} \right) X×nA×nB=X×n(BA) ② 特殊地,矩阵情形为: A B C = B × 1 A × 2 C T \mathbf{A B C}=\mathbf{B} \times_{1} \mathbf{A} \times_{2} \mathbf{C}^{\mathrm{T}} ABC=B×1A×2CT x T A y = A × 1 x T × 2 y T = A × 1 x × 2 y \mathbf{x}^{\mathrm{T}} \mathbf{A} \mathbf{y}=\mathbf{A} \times_{1} \mathbf{x}^{\mathrm{T}} \times_{2} \mathbf{y}^{\mathrm{T}}=\mathbf{A} \times_{1} \mathbf{x} \times_{2} \mathbf{y } xTAy=A×1xT×2yT=A×1x×2y 9.2 n模向量积(The n-mode vector product)(1)定义 张量 X ∈ R I 1 × I 2 × ⋯ × I N \mathscr{X} \in \mathbb{R}^{I_{1} \times I_{2} \times \cdots \times I_{N}} X∈RI1×I2×⋯×IN 与向量 v ∈ R I n \mathbf{v} \in\mathbb{R}^{I_{n}} v∈RIn 的n模(向量)积记为 X × ‾ n v \mathscr{X} \overline{\times}_{n} \mathbf{v} X×nv ,尺寸为 I 1 × ⋯ × I n − 1 × I n + 1 × ⋯ × I N I_{1} \times \cdots \times I_{n-1} \times I_{n+1} \times \cdots \times I_{N} I1×⋯×In−1×In+1×⋯×IN 。从元素上看有: ( X × ‾ n v ) i 1 ⋯ i n − 1 i n + 1 ⋯ i N = ∑ i n = 1 I n x i 1 i 2 ⋯ i N v i n \left(\mathscr{X} \overline{\times}_{n} \mathbf{v}\right)_{i_{1} \cdots i_{n-1} i_{n+1} \cdots i_{N}}=\sum_{i_{n}=1}^{I_{n}} x_{i_{1} i_{2} \cdots i_{N}} v_{i_{n}} (X×nv)i1⋯in−1in+1⋯iN=in=1∑Inxi1i2⋯iNvin (2)例题 设张量 x ∈ R 3 × 4 × 2 \mathscr{x} \in \mathbb{R}^{3 \times 4 \times 2} x∈R3×4×2 的前切片为: X 1 = [ 1 4 7 10 2 5 8 11 3 6 9 12 ] , X 2 = [ 13 16 19 22 14 17 20 23 15 18 21 24 ] \mathbf{X}_{1} = \left[\begin{array}{llll} 1 & 4 & 7 & 10 \\ 2 & 5 & 8 & 11 \\ 3 & 6 & 9 & 12 \end{array}\right] , \quad \mathbf{X}_{2} = \left[\begin{array}{llll} 13 & 16 & 19 & 22 \\ 14 & 17 & 20 & 23 \\ 15 & 18 & 21 & 24 \end{array}\right] X1=⎣⎡123456789101112⎦⎤,X2=⎣⎡131415161718192021222324⎦⎤ 向量: v = [ 1 2 3 4 ] T \mathbf{v}=\begin{bmatrix}1&2&3&4\end{bmatrix}^{T} v=[1234]T 则张量与向量的2模乘为: X × ‾ 2 v = [ 70 190 80 200 90 210 ] \mathscr{X}\overline{\times}_{2}\mathbf{v}=\begin{bmatrix}70&190\\80&200\\90&210 \end{bmatrix} X×2v=⎣⎡708090190200210⎦⎤ (3)基本运算法则 当涉及到模n向量乘法时,优先级很重要,因为中间结果的顺序会改变。即 X × ‾ m a × ‾ n b = ( X × ‾ m a ) × ‾ n − 1 b = ( X × ‾ n b ) × ‾ m a for m < n \mathscr{X} \overline{\times}_{m} \mathbf{a} \overline{\times}_{n} \mathbf{b}=\left(\mathscr{X} \overline{\times}_{m} \mathbf{a}\right) \overline{\times}_{n-1} \mathbf{b}=\left(\mathscr{X} \overline{\times}_{n} \mathbf{b}\right) \overline{\times}_{m} \mathbf{a} \text { for } m |
【本文地址】
今日新闻 |
点击排行 |
|
推荐新闻 |
图片新闻 |
|
专题文章 |