一文看懂 LLaMA 中的旋转式位置编码(Rotary Position Embedding) |
您所在的位置:网站首页 › 位置embedding › 一文看懂 LLaMA 中的旋转式位置编码(Rotary Position Embedding) |
一文看懂 LLaMA 中的旋转式位置编码(Rotary Position Embedding)
旋转式位置编码(RoPE)最早是论文[1]提出的一种能够将相对位置信息依赖集成到 self-attention 中并提升 transformer 架构性能的位置编码方式。而目前很火的 LLaMA 模型也是采用该位置编码方式。 接下来结合代码和论文来解读一下 RoPE。 基本概念首先论文中定义一个长度为 N 的输入序列为: S_{N}=\{ w_i \}_{i=1}^{N}其中 wi 表示输入序列中第 i 个 token,而输入序列 SN 对应的 embedding 表示为: E_{N}=\{ x_i \}_{i=1}^N其中 xi 表示第 i 个 token wi 对应的 d 维词嵌入向量。 接着在做 self-attention 之前,会用词嵌入向量计算 q, k, v 向量同时加入位置信息,函数公式表达如下: \begin{aligned} q_m=f_q(x_m,m) \\ k_n=f_k(x_n,n) \\ v_n=f_v(x_n,n) \end{aligned}其中 qm 表示第 m 个 token 对应的词向量 xm 集成位置信息 m 之后的 query 向量。而 kn 和 vn 则表示第 n 个 token 对应的词向量 xn 集成位置信息 n 之后的 key 和 value 向量。 而基于 transformer 的位置编码方法都是着重于构造一个合适的 f{q,k,v} 函数形式。 而计算第 m 个词嵌入向量 xm 对应的 self-attention 输出结果,就是 qm 和其他 kn 都计算一个 attention score ,然后再将 attention score 乘以对应的 vn 再求和得到输出向量 om: \begin{aligned} a_{m,n}=\frac{exp(\frac{q_m^Tk_n}{\sqrt{d}})}{\sum_{j=1}^Nexp(\frac{q_m^Tk_j}{\sqrt{d}})} \\ o_m=\sum_{n=1}^Na_{m,n}v_n \end{aligned}绝对位置编码 对于位置编码,常规的做法是在计算 query, key 和 value 向量之前,会计算一个位置编码向量 pi 加到词嵌入 xi 上,位置编码向量 pi 同样也是 d 维向量,然后再乘以对应的变换矩阵 W{q,k,v}: f_{\{q,k,v\}}(x_i,i)=W_{\{q,k,v\}}(x_i+p_i)而经典的位置编码向量 pi 的计算方式是: \begin{aligned} p_{i,2t}=sin(\frac{i}{10000^{\frac{2t}{d}}})\\ p_{i,2t+1}=cos(\frac{i}{10000^{\frac{2t}{d}}}) \end{aligned}其中 p_{i,2t} 表示位置 d 维度向量 pi 中的第 2t 个元素也就是偶数索引位置的计算公式,而 p_{i,2t+1} 就对应奇数索引位置的计算公式。 python 代码如下: 代码语言:javascript复制# position 就对应 token 序列中的位置索引 i # hidden_dim 就对应词嵌入维度大小 d # seq_len 表示 token 序列长度 def get_position_angle_vec(position): return [position / np.power(10000, 2 * (hid_j // 2) / hidden_dim) for hid_j in range(hidden_dim)] # position_angle_vecs.shape = [seq_len, hidden_dim] position_angle_vecs = np.array([get_position_angle_vec(pos_i) for pos_i in range(seq_len)]) # 分别计算奇偶索引位置对应的 sin 和 cos 值 position_angle_vecs[:, 0::2] = np.sin(position_angle_vecs[:, 0::2]) # dim 2t position_angle_vecs[:, 1::2] = np.cos(position_angle_vecs[:, 1::2]) # dim 2t+1 # positional_embeddings.shape = [1, seq_len, hidden_dim] positional_embeddings = torch.FloatTensor(position_angle_vecs).unsqueeze(0) 旋转式位置编码接着论文中提出为了能利用上 token 之间的相对位置信息,假定 query 向量 qm 和 key 向量 kn 之间的内积操作可以被一个函数 g 表示,该函数 g 的输入是词嵌入向量 xm , xn 和它们之间的相对位置 m - n: \lt f_q(x_m,m),f_k(x_n,n)\gt =g(x_m,x_n,m-n)接下来的目标就是找到一个等价的位置编码方式,从而使得上述关系成立。 假定现在词嵌入向量的维度是两维 d=2,这样就可以利用上2维度平面上的向量的几何性质,然后论文中提出了一个满足上述关系的 f 和 g 的形式如下: \begin{aligned} f_q(x_m,m)=(W_qx_m)e^{im\theta} \\ f_k(x_n,n)=(W_kx_n)e^{in\theta} \\ g(x_m,x_n,m-n)= \\Re[(W_qx_m)(W_kx_n)^{*}e^{i(m-n)\theta}] \end{aligned}上面的公式一眼看过去感觉很复杂,怎么理解呢? 首先我们得先了解一下基本的复数相关知识。 首先看到上述 f 和 g 公式中有个指数函数 e^{ix}这个其实是欧拉公式 [2],其中 x 表示任意实数, e 是自然对数的底数,i 是复数中的虚数单位,则根据欧拉公式有: e^{ix} = \cos x + i\sin x上述指数函数可以表示为实部为 cosx,虚部为 sinx 的一个复数,欧拉公式 [2] 建立了指数函数、三角函数和复数之间的桥梁。 则上述 f 和 g 公式中的 \begin{aligned} e^{im\theta}=\cos (m\theta) + i\sin (m\theta) \\ e^{in\theta}=\cos (n\theta) + i\sin (n\theta) \\ e^{i(m-n)\theta}=\cos ((m-n)\theta) + i\sin ((m-n)\theta) \end{aligned}然后我们看回公式: f_q(x_m,m)=(W_qx_m)e^{im\theta} \\其中 Wq 是个二维矩阵,xm 是个二维向量,相乘的结果也是一个二维向量,这里用 qm 表示: \begin{aligned} q_m= \begin{pmatrix} q_m^{(1)} \\ q_m^{(2)} \end{pmatrix} = W_qx_m =\begin{pmatrix} W_q^{(11)} & W_q^{(12)} \\ W_q^{(21)} & W_q^{(22)} \end{pmatrix} \begin{pmatrix} x_m^{(1)} \\ x_m^{(2)} \end{pmatrix} \end{aligned}然后首先将 qm 表示成复数形式: q_m = [q_m^{(1)}, q_m^{(2)}] = [q_m^{(1)} + iq_m^{(2)}]接着 f_q(x_m,m)=(W_qx_m)e^{im\theta}=q_me^{im\theta} \\其实就是两个复数相乘: q_me^{im\theta}=(q_m^{(1)} + iq_m^{(2)}) * (\cos (m\theta) + i\sin (m\theta))我们首先来复习一下复数乘法的性质: (a+ib) \cdot (c+id) = ac + ibc + iad + i^2bd=(ac-bd)+i(bc+ad)可以看到,复数乘法也是用的分配律,还有用到了复数的一个性质: i^2=-1然后就有: \begin{aligned} q_me^{im\theta}=(q_m^{(1)} + iq_m^{(2)}) * (\cos (m\theta) + i\sin (m\theta)) \\ =(q_m^{(1)}cos (m\theta) - q_m^{(2)} \sin (m\theta) ) + i(q_m^{(2)}\cos (m\theta) + q_m^{(1)}\sin (m\theta)) \end{aligned}将结果重新表达成实数向量形式就是: \begin{aligned} q_me^{im\theta}=[q_m^{(1)} \cos (m\theta) - q_m^{(2)} \sin (m\theta), q_m^{(2)}\cos (m\theta) + q_m^{(1)}\sin (m\theta)] \end{aligned}相信读者看到这里会发现这不就是 query 向量乘以了一个旋转矩阵[5]吗? \begin{aligned} f_q(x_m,m)=(W_qx_m)e^{im\theta}=q_me^{im\theta}\\ =[q_m^{(1)} \cos (m\theta) - q_m^{(2)} \sin (m\theta), q_m^{(2)}\cos (m\theta) + q_m^{(1)}\sin (m\theta)] \\ = \begin{pmatrix} \cos (m\theta) & -\sin (m\theta) \\ \sin (m\theta) & \cos (m\theta) \end{pmatrix} \begin{pmatrix} q_m^{(1)} \\ q_m^{(2)} \end{pmatrix}\end{aligned}这就是为什么叫做旋转式位置编码的原因。 同理可得 key 向量 kn : \begin{aligned} f_k(x_n,n)=(W_kx_n)e^{in\theta}=k_ne^{in\theta}\\ =[k_n^{(1)} \cos (n\theta) - k_n^{(2)} \sin (n\theta), k_n^{(2)}\cos (n\theta) + k_n^{(1)}\sin (n\theta)] \\ = \begin{pmatrix} \cos (n\theta) & -\sin (n\theta) \\ \sin (n\theta) & \cos (n\theta) \end{pmatrix} \begin{pmatrix} k_n^{(1)} \\ k_n^{(2)} \end{pmatrix}\end{aligned}最后还有个函数 g: g(x_m,x_n,m-n)=Re[(W_qx_m)(W_kx_n)^{*}e^{i(m-n)\theta}]其中 Re[x] 表示一个复数 x 的实部部分,而 (W_kx_n)^{*}则表示复数 W_kx_n的共轭,复习一下共轭复数的定义: \begin{aligned} z=a+ib\\ z^*=a-ib \end{aligned}所以可得: \begin{aligned} W_qx_m = q_m = q_m^{(1)} + iq_m^{(2)} \\ W_kx_n=k_n= k_n^{(1)} + ik_n^{(2)} \\ (W_kx_n)^*=k_n^*= k_n^{(1)} - ik_n^{(2)} \\ e^{i(m-n)\theta}=\cos((m-n)\theta) + i \sin((m-n)\theta) \end{aligned}继续可得: \begin{aligned} g(x_m,x_n,m-n)=Re[(W_qx_m)(W_kx_n)^{*}e^{i(m-n)\theta}] \\ = Re[(q_m^{(1)} + iq_m^{(2)})(k_n^{(1)} - ik_n^{(2)})(\cos((m-n)\theta) + i \sin((m-n)\theta))] \\ = Re[((q_m^{(1)}k_n^{(1)} + q_m^{(2)}k_n^{(2)}) + i(q_m^{(2)}k_n^{(1)} - q_m^{(1)}k_n^{(2)}))(\cos((m-n)\theta) + i \sin((m-n)\theta))] \\ = (q_m^{(1)}k_n^{(1)} + q_m^{(2)}k_n^{(2)})\cos((m-n)\theta) - (q_m^{(2)}k_n^{(1)} - q_m^{(1)}k_n^{(2)})\sin((m-n)\theta)\end{aligned}ok,接下来我们就要证明函数 g 的计算公式是成立的。 首先回顾一下 attention 操作, 位置 m 的 query 和位置 n 的 key 会做一个内积操作: \begin{aligned} f_q(x_m,m)=[q_m^{(1)} \cos (m\theta) - q_m^{(2)} \sin (m\theta), q_m^{(2)}\cos (m\theta) + q_m^{(1)}\sin (m\theta)] \\ f_k(x_n,n) =[k_n^{(1)} \cos (n\theta) - k_n^{(2)} \sin (n\theta), k_n^{(2)}\cos (n\theta) + k_n^{(1)}\sin (n\theta)] \\ \lt f_q(x_m,m),f_k(x_n,n) \gt = \\ (q_m^{(1)} \cos (m\theta) - q_m^{(2)} \sin (m\theta))(k_n^{(1)} \cos (n\theta) - k_n^{(2)} \sin (n\theta)) \\+ (q_m^{(2)}\cos (m\theta) + q_m^{(1)}\sin (m\theta))(k_n^{(2)}\cos (n\theta) + k_n^{(1)}\sin (n\theta))\\ =q_m^{(1)} \cos (m\theta) k_n^{(1)} \cos (n\theta) - q_m^{(1)} \cos (m\theta)k_n^{(2)} \sin (n\theta)\\ - q_m^{(2)} \sin (m\theta)k_n^{(1)} \cos (n\theta) + q_m^{(2)} \sin (m\theta)k_n^{(2)} \sin (n\theta) \\ + q_m^{(2)}\cos (m\theta)k_n^{(2)}\cos (n\theta) + q_m^{(2)}\cos (m\theta)k_n^{(1)}\sin (n\theta) \\ + q_m^{(1)}\sin (m\theta)k_n^{(2)}\cos (n\theta) + q_m^{(1)}\sin (m\theta)k_n^{(1)}\sin (n\theta) \end{aligned} \begin{aligned} f_q(x_m,m)=[q_m^{(1)} \cos (m\theta) - q_m^{(2)} \sin (m\theta), q_m^{(2)}\cos (m\theta) + q_m^{(1)}\sin (m\theta)] \\ f_k(x_n,n) =[k_n^{(1)} \cos (n\theta) - k_n^{(2)} \sin (n\theta), k_n^{(2)}\cos (n\theta) + k_n^{(1)}\sin (n\theta)] \\= \\ (q_m^{(1)} \cos (m\theta) - q_m^{(2)} \sin (m\theta))(k_n^{(1)} \cos (n\theta) - k_n^{(2)} \sin (n\theta)) \\+ (q_m^{(2)}\cos (m\theta) + q_m^{(1)}\sin (m\theta))(k_n^{(2)}\cos (n\theta) + k_n^{(1)}\sin (n\theta))\\ =q_m^{(1)} \cos (m\theta) k_n^{(1)} \cos (n\theta) - q_m^{(1)} \cos (m\theta)k_n^{(2)} \sin (n\theta)\\ - q_m^{(2)} \sin (m\theta)k_n^{(1)} \cos (n\theta) + q_m^{(2)} \sin (m\theta)k_n^{(2)} \sin (n\theta) \\ + q_m^{(2)}\cos (m\theta)k_n^{(2)}\cos (n\theta) + q_m^{(2)}\cos (m\theta)k_n^{(1)}\sin (n\theta) \\ + q_m^{(1)}\sin (m\theta)k_n^{(2)}\cos (n\theta) + q_m^{(1)}\sin (m\theta)k_n^{(1)}\sin (n\theta) \end{aligned}接着继续之前先复习一下三角函数的一些性质[3]: \begin{aligned} \sin(a+b) = \sin a \cos b + \cos a \sin b \\ \sin(a-b) = \sin a \cos b - \cos a \sin b \\ \cos(a+b) = \cos a \cos b - \sin a \sin b \\ \cos(a-b) = \cos a \cos b + \sin a \sin b \end{aligned}好了回到上面那坨式子,我们整理一下: \begin{aligned} \lt f_q(x_m,m),f_k(x_n,n) \gt = \\ q_m^{(1)}k_n^{(1)}(\cos(m\theta)\cos(n\theta) + \sin(m\theta)\sin(n\theta) ) \\ + q_m^{(1)}k_n^{(2)}(-\cos(m\theta)\sin(n\theta) + \sin(m\theta)\cos(n\theta) ) \\ + q_m^{(2)}k_n^{(1)}(-\sin(m\theta)\cos(n\theta) + \cos(m\theta)\sin(n\theta) ) \\ + q_m^{(2)}k_n^{(2)}(\sin(m\theta)\sin(n\theta) + \cos(m\theta)\cos(n\theta) ) \\ = q_m^{(1)}k_n^{(1)}\cos((m-n)\theta) \\ + q_m^{(1)}k_n^{(2)}\sin((m-n)\theta) \\ - q_m^{(2)}k_n^{(1)}\sin((m-n)\theta) \\ + q_m^{(2)}k_n^{(2)}\cos((m-n)\theta) \\ = (q_m^{(1)}k_n^{(1)} + q_m^{(2)}k_n^{(2)})\cos((m-n)\theta) + (q_m^{(1)}k_n^{(2)}- q_m^{(2)}k_n^{(1)})\sin((m-n)\theta) \\ = (q_m^{(1)}k_n^{(1)} + q_m^{(2)}k_n^{(2)})\cos((m-n)\theta) - (q_m^{(2)}k_n^{(1)} - q_m^{(1)}k_n^{(2)})\sin((m-n)\theta) \\ =g(x_m,x_n,m-n) \end{aligned}这就证明上述关系是成立的,位置 m 的 query 和位置 n 的 key 的内积就是函数 g。 然后上面的讲解是假定的词嵌入维度是2维向量,而对于d >= 2 的通用情况,则是将词嵌入向量元素按照两两一组分组,每组应用同样的旋转操作且每组的旋转角度计算方式如下: \theta_j=10000^{-2(j-1)/d}, j \in [1,2,...,d/2]所以简单来说 RoPE 的 self-attention 操作的流程是,对于 token 序列中的每个词嵌入向量,首先计算其对应的 query 和 key 向量,然后对每个 token 位置都计算对应的旋转位置编码,接着对每个 token 位置的 query 和 key 向量的元素按照 两两一组 应用旋转变换,最后再计算 query 和 key 之间的内积得到 self-attention 的计算结果。 论文中有个很直观的图片展示了旋转变换的过程: 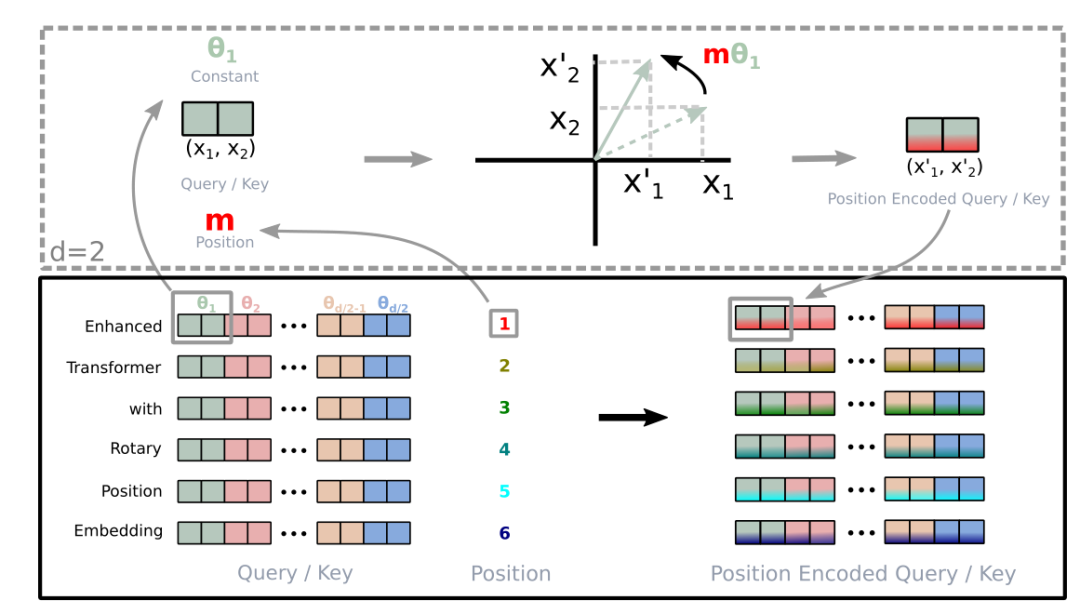 LLaMA 官方实现代码 [4] 如下(经过简化): 代码语言:javascript复制def precompute_freqs_cis(dim: int, seq_len: int, theta: float = 10000.0): # 计算词向量元素两两分组之后,每组元素对应的旋转角度 freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim)) # 生成 token 序列索引 t = [0, 1,..., seq_len-1] t = torch.arange(seq_len, device=freqs.device) # freqs.shape = [seq_len, dim // 2] freqs = torch.outer(t, freqs).float() # torch.polar 的文档 # https://pytorch.org/docs/stable/generated/torch.polar.html # 计算结果是个复数向量 # 假设 freqs = [x, y] # 则 freqs_cis = [cos(x) + sin(x)i, cos(y) + sin(y)i] freqs_cis = torch.polar(torch.ones_like(freqs), freqs) return freqs_cis def apply_rotary_emb( xq: torch.Tensor, xk: torch.Tensor, freqs_cis: torch.Tensor, ) -> Tuple[torch.Tensor, torch.Tensor]: # xq.shape = [batch_size, seq_len, dim] # xq_.shape = [batch_size, seq_len, dim // 2, 2] xq_ = xq.float().reshape(*xq.shape[:-1], -1, 2) xk_ = xk.float().reshape(*xk.shape[:-1], -1, 2) # 转为复数域 xq_ = torch.view_as_complex(xq_) xk_ = torch.view_as_complex(xk_) # 应用旋转操作,然后将结果转回实数域 # xq_out.shape = [batch_size, seq_len, dim] xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(2) xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(2) return xq_out.type_as(xq), xk_out.type_as(xk) class Attention(nn.Module): def __init__(self, args: ModelArgs): super().__init__() self.wq = Linear(...) self.wk = Linear(...) self.wv = Linear(...) self.freqs_cis = precompute_freqs_cis(dim, max_seq_len * 2) def forward(self, x: torch.Tensor): bsz, seqlen, _ = x.shape xq, xk, xv = self.wq(x), self.wk(x), self.wv(x) xq = xq.view(batch_size, seq_len, dim) xk = xk.view(batch_size, seq_len, dim) xv = xv.view(batch_size, seq_len, dim) # attention 操作之前,应用旋转位置编码 xq, xk = apply_rotary_emb(xq, xk, freqs_cis=freqs_cis) # scores.shape = (batch_size, seq_len, seqlen) scores = torch.matmul(xq, xk.transpose(1, 2)) / math.sqrt(dim) scores = F.softmax(scores.float(), dim=-1) output = torch.matmul(scores, xv) # (batch_size, seq_len, dim) # ......可以看到 LLaMA 的官方实现代码和论文 [1] 中的描述是一致的。 参考资料[1] https://arxiv.org/pdf/2104.09864.pdf[2] https://en.wikipedia.org/wiki/Euler's_formula[3] https://en.wikipedia.org/wiki/List_of_trigonometric_identities[4] https://github.com/facebookresearch/llama/tree/main[5] https://zh.wikipedia.org/wiki/旋转矩阵 |
【本文地址】
今日新闻 |
点击排行 |
|
推荐新闻 |
图片新闻 |
|
专题文章 |