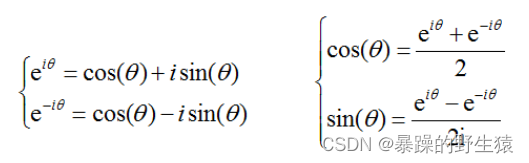| 概念:微分方程的解、瞬态响应、稳态响应、自由响应、强迫响应、零输入响应、零状态响应 | 您所在的位置:网站首页 › 齐次方程的特解和通解的关系 › 概念:微分方程的解、瞬态响应、稳态响应、自由响应、强迫响应、零输入响应、零状态响应 |
概念:微分方程的解、瞬态响应、稳态响应、自由响应、强迫响应、零输入响应、零状态响应
|
要理解这几个概念,首先要从“微分方程的解“的结构说起, 参考:《常系数线性微分方程的解法》
我们对物理系统进行建模时,列出的微分方程多为”非齐次、线性“,如上式(2)所示,由上面的定理7可知,这种非齐次微分方程的通解y(t)由两部分相加:①对应的”齐次微分方程“的通解y1(t),②一个该非齐次微分方程的特解y2(t)。 y(t)就是该物理系统的输出信号的时域表达式,显然该表达式中的y1(t)部分跟输入信号f(t)无关,那么y1(t)就称为该系统的”自由响应“,y2(t)跟输入信号f(t)相关,称为系统在输入信号作用下的”强迫响应“,《机械工程控制基础》第6版,p83最后一段 关于特征根:按照”线性微分方程的解”相关理论,对齐次方程做拉氏变换后,可以得到一个关于复变量s的代数方程,我们知道,“方程的解的形式”与“这个s代数方程的根的情况”直接相关,所以我们把这个代数方程(特征方程)的根称为特征根。那么这两者的关系是什么?如下所示: ①特征根均为单实根,则齐次微分方程的解的形式一定是: ②特征根为一重共轭复根,形如α±βi,则齐次微分方程的解的形式一定是: ③特征根为k重根(还可细分为k重实根/k重复根),则解的形式是: 实际上以上种种情况都是③的特例,直接看一个特征方程的例子,特征方程是以s为变量的高次多项式: 一个高次多项式,在复数域内一定可以进行因式分解,化为这种形式:
题外话:为什么一定能因式分解为上述形式,例如:
下面回到正题,继续看上面的③, 式(3)总共有k1+k2+```+kn个复数根,这些ki中可能有一些为0,这样相应的特征根λi就变成了单重根,否则就是ki重根;如果某个特征根λi的虚部为0,那么λi就是ki重实根。显然根据ki的不同、λi实虚部的不同,可以涵盖前面所述的三种情况。 直接给出结论得了,式(3)对应的齐次微分方程的解的基为: 也即,微分方程的解为:上图中的每一项*cij,再相加(如果λi含虚部,还可把e^λit进一步欧拉展开)。 利用这条结论,我们来做几个例子: 例1:已知某齐次线性微分方程的特征方程为(s-5)(s+3)^2=0,问该微分方程的解?
分析:特征根为:λ1=5 (重数k1=1)、λ2= -3(k2=2),那么根据上图,我们可以写出微分方程的解空间的基为:
从而得到解为: 例2:已知某齐次线性微分方程的特征方程为(s-5)(s^2+2s+5)^2=0,问该微分方程的解? 该特征方程的根为: λ1=-1+2j (重数k1=2)、λ2=-1-2j (重数k2=2)、λ3=5 (重数k3=1),那么根据上图写出解的基为: 根据解的基,可以立即写出微分方程的通解: 总结一下齐次线性微分方程的解的结构:一定脱离不了这种形式的多项式:
由上述分析可见,基础解系的线性组合就是通解,不过令人疑惑的是,基础解系中含有虚数i,也即最终方程的解类似这样:y(t) = sin(2*t) + 5 * i * cos(8*t) +.....。这很奇怪,对于yt=f(t)这种一元非线性函数,是很容易绘制出时域曲线的,但是表达式中含有虚数i,就让人不知所措了,想象不出这条曲线到底长啥样,甚至不知道这个函数式到底能不能画出曲线。 其实这个问题的解决方案也很简单:由于这些含有虚数的解,一定是共轭的,通过合并同类项,一定能用欧拉公式,把指数部分含虚数的项,合并为三角函数sin或cos 附一个欧拉公式
下面再继续讲解概念:瞬态响应。 根据(式10)可知,只要特征根的实部 |
【本文地址】
| 今日新闻 |
| 推荐新闻 |
| 专题文章 |
 (1)
(1) (2)
(2)
 在实数域无法分解,但在复数域就能分解为:
在实数域无法分解,但在复数域就能分解为: