| 2023 | 您所在的位置:网站首页 › 非线性计算不收敛 › 2023 |
2023
|
2023-06-30《计算方法》- 陈丽娟 - 线性方程组的迭代解法Matlab计算方法JacobiGauss-SeidelSORSSOR定常迭代法 所谓迭代法实际上是求解一个关于映射  然后利用
然后利用 构造一个迭代格式 构造一个迭代格式
 这里
这里 表示T的一个复合函数, 其可能随迭代次数而改变,最终目标即是得到 表示T的一个复合函数, 其可能随迭代次数而改变,最终目标即是得到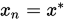 . 下面我们给出收敛的定义:
定义1
设 . 下面我们给出收敛的定义:
定义1
设 , , 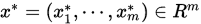 , 若 , 若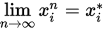 , , 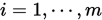 , 则称点列 , 则称点列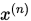 收敛于 收敛于 , 记作 , 记作 . .
定理1
序列 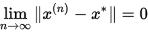 1. 雅可比迭代法
1. 雅可比迭代法
对于非奇异线性方程组 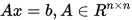 令
令
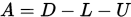 其中
其中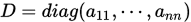 , , 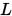 为 为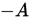 的下三角矩阵, 的下三角矩阵,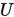 为 为 的上三角矩阵。
则有 的上三角矩阵。
则有
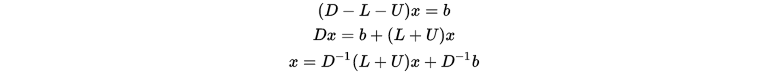 给定
给定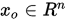 , 下述迭代格式称为雅可比迭代: , 下述迭代格式称为雅可比迭代:
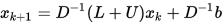 注意上式很容易可以写出个分量的迭代格式:
注意上式很容易可以写出个分量的迭代格式:
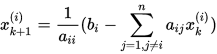 2. 高斯-赛德尔迭代
2. 高斯-赛德尔迭代
在雅可比迭代中,如果  其矩阵形式为
其矩阵形式为
 即是
即是
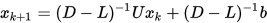 3. Jacobi和G-S迭代的统一框架
3. Jacobi和G-S迭代的统一框架
矩阵分裂
设  为
为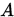 的一个矩阵分裂,其中 的一个矩阵分裂,其中 非奇异。 非奇异。
对于 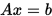 经过矩阵分裂可得
经过矩阵分裂可得
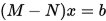 移项可得
移项可得
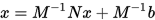
由上可知雅可比迭代就是取 为了加速迭代的收敛,SOR方法将G-S迭代中  上式整理之后可得
上式整理之后可得
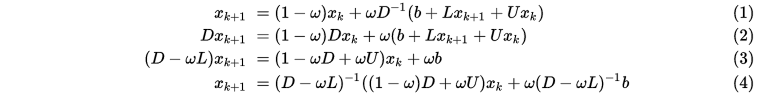
同样可以得到对应的 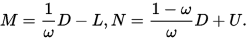 迭代格式为
迭代格式为
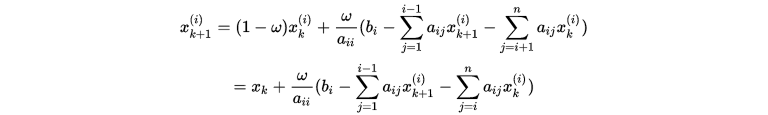
其中 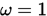 时,即是G-S迭代法;
当 时,即是G-S迭代法;
当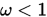 时,称为低松弛方法;
当 时,称为低松弛方法;
当 时,称为超松弛方法(大部分情况下超松弛更好)。 时,称为超松弛方法(大部分情况下超松弛更好)。
注意到一开始SOR方法实际上是一个MANN迭代( 将 SOR 方法中的  结合上式和SOR则得到SSOR(对称超松弛迭代法)
结合上式和SOR则得到SSOR(对称超松弛迭代法)
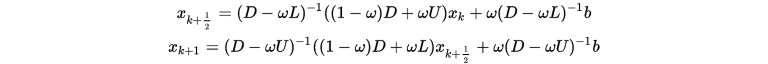
注
对于某些特殊问题, SOR 方法不收敛, 但仍然可能构造出收敛的 SSOR 方法.
一般来说, SOR 方法的渐进收敛速度对参数 从不动点理论的角度来看,上述所有的迭代格式都可以看作是 下面根据华东师范大学潘建瑜老师《矩阵计算讲义》列出矩阵下的收敛性分析,我们可以看到虽然描述的方式不一样,但是和不动点理论的结果却是相似的。 矩阵序列的收敛 设 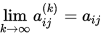 则称
则称 收敛到 收敛到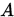 , 即 , 即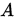 是 是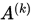 的极限,记为 的极限,记为
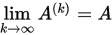 . .
定理
设矩阵 定理
设 
收敛速度
设点列 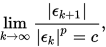 则称点列
则称点列 是p次(渐进)收敛的. 若 是p次(渐进)收敛的. 若 或 或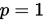 且 且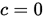 ,则称点列是超线性收敛的。 ,则称点列是超线性收敛的。
收敛性定理
对任意迭代初始向量 定义
设  渐进收敛速度定义为
渐进收敛速度定义为

定理
考虑矩阵分裂迭代法,如果存在某个算子范数 
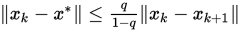
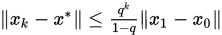 6. 各迭代法之间的数值比较
6. 各迭代法之间的数值比较
下面给出的算法包含求逆运算,用行迭代是否可以加速计算有待深入。 Jacobi迭代法 function [x0, xlog] = JacobiLE(x0, A, b, epsilon, maxit) if(nargin < 5) maxit = 1e3; end iter = 1; xlog = zeros(maxit,1); errors = norm(A*x0 - b); D = diag(diag(A)); LU = D - A; D = inv(D); G = D * LU; F = D * b; while iter = epsilon %x1 = G * x0 + F; x1 = x0 + D * (b - A*x0); errors = norm(A * x1 - b); xlog(iter) = errors; x0 = x1; iter = iter + 1; end xlog = xlog(1:(iter-1)); endG-S迭代法 function [x0, xlog] = GSLE(x0, A, b, epsilon, maxit) if(nargin < 5) maxit = 1e3; end iter = 1; xlog = zeros(maxit,1); errors = norm(A*x0 - b); D = diag(diag(A)); L = D - tril(A); U = D - triu(A); DL = inv(D-L); G = DL * U; F = DL * b; while iter = epsilon x1 = G * x0 + F; %x1 = x0 + D * (b - A*x0); errors = norm(A * x1 - b); xlog(iter) = errors; x0 = x1; iter = iter + 1; end xlog = xlog(1:(iter-1)); endSOR迭代法 function [x0, xlog] = SOR(x0, A, b, omega, epsilon, maxit) if(nargin < 6) maxit = 1e3; end iter = 1; xlog = zeros(maxit,1); errors = norm(A*x0 - b); D = diag(diag(A)); L = D - tril(A); U = D - triu(A); DL = inv(D-omega *L); G = DL * ((1-omega)*D+omega*U); F = omega * DL * b; while iter = epsilon x1 = G * x0 + F; %x1 = x0 + D * (b - A*x0); errors = norm(A * x1 - b); xlog(iter) = errors; x0 = x1; iter = iter + 1; end xlog = xlog(1:(iter-1)); endSSOR迭代法 function [x0, xlog] = SSOR(x0, A, b, omega, epsilon, maxit) if(nargin < 6) maxit = 1e3; end iter = 1; xlog = zeros(maxit,1); errors = norm(A*x0 - b); D = diag(diag(A)); L = D - tril(A); U = D - triu(A); DL = inv(D-omega*L); DU = inv(D-omega*U); GL = DL * ((1-omega)*D+omega*U); GU = DU * ((1-omega)*D+omega*L); FL = omega * DL * b; FU = omega * DU * b; while iter = epsilon x1 = GL * x0 + FL; x1 = GU * x1 + FU; %x1 = x0 + D * (b - A*x0); errors = norm(A * x1 - b); xlog(iter) = errors; x0 = x1; iter = iter + 1; end xlog = xlog(1:(iter-1)); end下面给出例子 clear n = 1000; x0 = rand(n,1); A = rand(n,n)*10; A = A + diag(sum(A,2)); max(abs(eig(A))); %谱半径 b = rand(n,1); epsilon = 1e-6; maxit = 1e3; [JacpbiX, JacobiXlog] = JacobiLE(x0, A, b, epsilon, maxit); plot(log10(JacobiXlog)) xlim([0 100]) hold on [GSS, GSSlog] = GSLE(x0, A, b, epsilon, maxit); plot(log10(GSSlog)) hold on omega = 1.5; [SORX, SORXlog] = SOR(x0, A, b, omega, epsilon, maxit); plot(log10(SORXlog)) hold on omega = 1.5; [SSORX, SSORXlog] = SSOR(x0, A, b, omega, epsilon, maxit); plot(log10(SSORXlog)) legend(["Jacobi" "G-S" "SOR" "SSOR"])结果如下所示
随机产生的矩阵很有可能在迭代过程中 定义
设 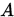 的元素满足 的元素满足 , 则称 , 则称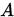 为严格(行)对角占优矩阵。(相应的可以定义列对角占优矩阵)
如果 为严格(行)对角占优矩阵。(相应的可以定义列对角占优矩阵)
如果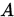 的元素满足 的元素满足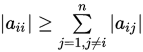 , 且至少对一个 , 且至少对一个 不等式严格成立,则称 不等式严格成立,则称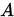 为弱对角占优矩阵 为弱对角占优矩阵
定义
设 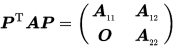 其中
其中 为r阶方阵, 为r阶方阵,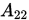 为 为 阶方阵,则称 阶方阵,则称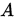 为可约矩阵,否则则称A为不可约矩阵。 为可约矩阵,否则则称A为不可约矩阵。
定理
设 |
【本文地址】
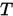 的不动点问题:
的不动点问题:
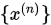 依坐标收敛(依范数收敛)于
依坐标收敛(依范数收敛)于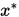 的充分条件是
的充分条件是
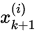 先被计算出来,则我们可以将分量
先被计算出来,则我们可以将分量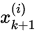 替换
替换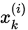 带入到
带入到 的计算中,即是
的计算中,即是
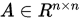 非奇异,称
非奇异,称
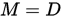 ,
, 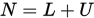 , 而G-S迭代是取
, 而G-S迭代是取 ,
, 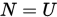 , 因此都可称为矩阵分裂迭代法。
, 因此都可称为矩阵分裂迭代法。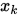 与
与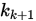 做一个凸组合作为下一步迭代的值,即是
做一个凸组合作为下一步迭代的值,即是
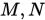
 不同取值时:
不同取值时: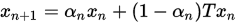 ),但是MANN迭代需要
),但是MANN迭代需要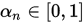 等条件,且MANN迭代的提出并非是为了加快收敛速度,而是为了解决Picard迭代在非扩张映射下不一定收敛而提出的。
等条件,且MANN迭代的提出并非是为了加快收敛速度,而是为了解决Picard迭代在非扩张映射下不一定收敛而提出的。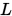 和
和  相互交换位置, 则可得迭代格式
相互交换位置, 则可得迭代格式
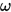 比较敏感, 但 SSOR 对参数
比较敏感, 但 SSOR 对参数 不是很敏感.
不是很敏感. , 其中
, 其中 , 即所有的迭代都是Picard迭代,那么根据Banach不动点定理,我们知道当
, 即所有的迭代都是Picard迭代,那么根据Banach不动点定理,我们知道当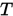 是压缩映射时(
是压缩映射时(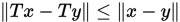 即
即 ),序列
),序列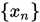 收敛到
收敛到 的不动点,也就是线性方程组的解。
的不动点,也就是线性方程组的解。 是
是 中的一个矩阵序列。如果存在矩阵
中的一个矩阵序列。如果存在矩阵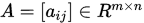 使得
使得
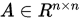 ,则
,则 当且仅当
当且仅当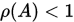 .
证明:
设
.
证明:
设 ,则存在矩阵范数
,则存在矩阵范数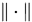 使得
使得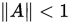 。因此
。因此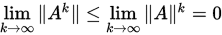 必要性:由
必要性:由 即可得。
即可得。 , 则对任意矩阵范数
, 则对任意矩阵范数 , 有
, 有
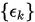 收敛,且
收敛,且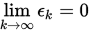 . 若存在一个有界常数
. 若存在一个有界常数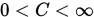 , 使得
, 使得
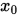 , 矩阵分裂迭代法收敛充要条件是
, 矩阵分裂迭代法收敛充要条件是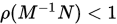 .
.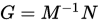 是迭代矩阵,则矩阵分裂迭代法的平均收敛速度定义为
是迭代矩阵,则矩阵分裂迭代法的平均收敛速度定义为
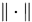 使得
使得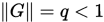 ,则
,则
 导致迭代发散,因此这里将随机矩阵改成了严格行对角占优矩阵,相关补充如下。
导致迭代发散,因此这里将随机矩阵改成了严格行对角占优矩阵,相关补充如下。 , 则有:
, 则有: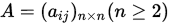 ,如果存在置换矩阵
,如果存在置换矩阵 , 使得
, 使得
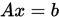 ,如果
,如果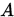 为严格对角占优矩阵,或
为严格对角占优矩阵,或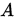 为弱对角占优矩阵且
为弱对角占优矩阵且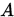 是不可约矩阵,则Jacobi和G-S迭代均收敛。
是不可约矩阵,则Jacobi和G-S迭代均收敛。