概率论与数理统计

随机变量就是随机事件的数值体现。

例如投色子记录色子的点数，记录的点数其实就是一个随机变量，他是这个点数出现的数值体现。

注意：

随机变量分为两种：连续型和离散型，跟函数的连续和间断类似。

随机变量的各个取值对应的概率称为分布律，可以作为计算公式 一般会用一个表格来表示

注意：

实验只有两种结果，取值用0和1表示 分布律为：

对一个只有 A 和 A ˉ A和\bar A A和Aˉ的事件进行n次实验，事件发生的次数服从二项分布 用表示 B ( n , p ) B(n,p) B(n,p)，事件不发生的概率为 1 − B ( n , p ) 1-B(n,p) 1−B(n,p) 分布律： P ( n , p ) = C n k ∗ p k ∗ ( 1 − p ) n − k P(n,p) = C_n^k * p^k * (1-p)^{n-k} P(n,p)=Cnk​∗pk∗(1−p)n−k(k为事件发生的次数)

泊松分布用于描述一定事件或者空间中事件发生次数的概率，用 Π ( λ ) Π(\lambda) Π(λ)表示（ λ \lambda λ为该时间或空间内事件发生的平均次数。） 分布律： P ( X = k ) = λ k e − λ k ! P(X = k) = \frac{\lambda^k e^{-\lambda}}{k!} P(X=k)=k!λke−λ​

泊松分布例题

当二项分布B(n,p)的n较大，且p较小时，二项分布大致服从泊松分布Π(np)

即 P ( X = k ) = C n k p k ( 1 − p ) n − k = ( n p ) k e − n p k ! P(X=k) = C_n^kp^k(1-p)^{n-k} = \frac{(np)^ke^{-np}}{k!} P(X=k)=Cnk​pk(1−p)n−k=k!(np)ke−np​

泊松定理例题

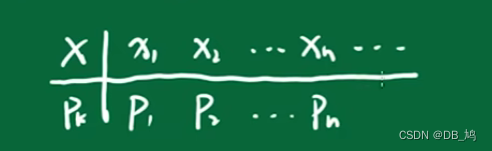
注释：