电磁场中达朗贝尔方程的求解及其应用

其中，

由于Maxwell方程组中电场 E 和磁场 B 相互耦合，直接求解空间中电磁场的分布较为复杂，因此需要引入一定的辅助量简化计算。根据Maxwell方程组中的方程（3），即磁场是一个无源场，可知存在一矢量场 A ，它满足：

且：

即矢量场 A 为磁场 B 的矢势，若求得 A 再对其取旋度则得到磁场 B 。

将式（3-1）带入Maxwell第二方程，得到：

式（3-2）表明这个新引入的矢量场是一个无旋场，可以将它表示为某一标量场 \varphi 的梯度场，即：

此时，引入了矢量函数 A 和标量函数 \varphi ，这两个辅助量可统一称作动态位，用它们可以表示空间中的电磁场 E 和 B ，即：

式（3-3）的导出利用了Maxwell方程组中的方程（2）和（3），因此再将它们带入方程（1）和（4），得到矢量函数 A 和标量函数 \varphi 与电磁场激励源（电荷 \rho 和电流 J ）之间的关系——

利用矢量运算恒等式：

由Maxwell方程（1）和（4）分别得到：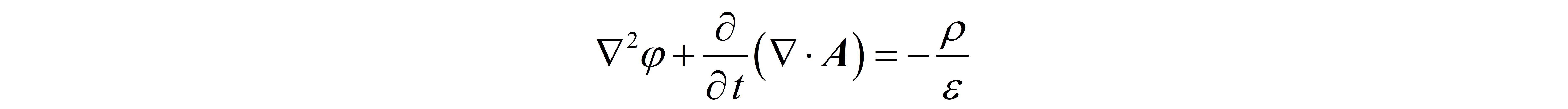

在式（3-4）的方程组中，矢量函数 A 和标量函数 \varphi 仍然相互耦合，为方便求解，需要找到它们分别单独满足的微分方程——

根据亥姆霍兹定理，空间中的某一矢量场由它的散度、旋度和边界条件唯一地确定。在前述中我们只规定了矢量场 A 的旋度，而其散度待定，所以此处要求矢量函数 A 和标量函数 \varphi 满足条件：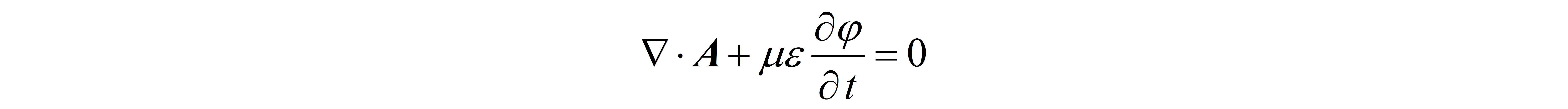

至此，公式（3-4）的方程组被简化为：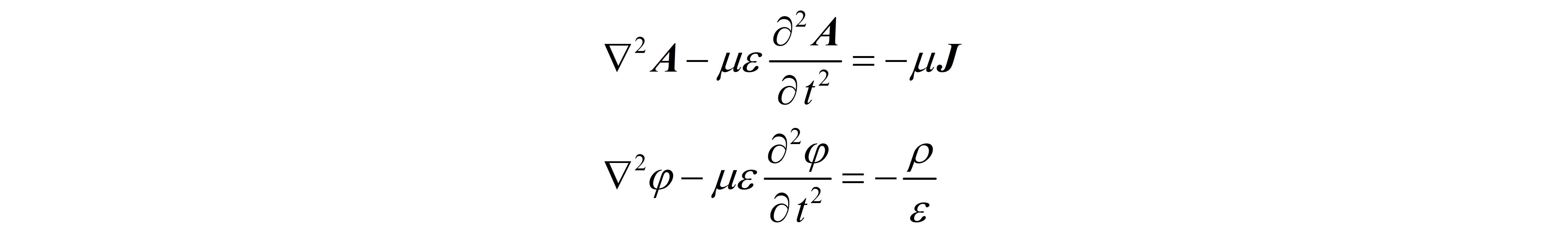

式（3-5）为矢量函数 A 和标量函数 \varphi 的达朗贝尔方程。这是两个非齐次的波动方程，通过它的求解，即可得到由激励源（电荷 \rho 和电流 J ）在空间中激发的电磁场。

在数学物理方法中，有一类描述振动或波动特征的波动方程，其形式为：

其中， u 是关于位置和时间的函数 u(x,y,z;t) ； u_{tt} 表示 u 对时间变量的二阶偏导数，记为 u_{tt}=\frac{\partial^{2}u}{\partial t^{2}} ； a 为方程中的系数，与波的传播速度有关； f=f(x,y,z;t) 是与源有关的已知函数，如引起振动的外力、电磁场的激励源等等。

与常微分方程的求解类似，我们首先能够求得上述偏微分方程的通解；另外，为了得到唯一确定的合理解，还需要定解条件。由于 u 是关于位置和时间的函数，我们可以直观地理解定解条件包括初始条件和边界条件，即初始时刻 t=0 的物理状态和整个物理过程的边界状况（因为边界状态将通过连续体逐点影响到所研究的整个区域）。

综上，求解这一类波动方程时，需要先求得方程的通解，然后利用定解条件得到方程的最终解，而“达朗贝尔方程”就属于这一类偏微分方程。由于源所引起的振动或波动会形成行波，向外传播至所研究的空间，因此将解决此类问题的方法称为“行波法”。

若式（4-1）方程的右侧 f=0 ，此时方程为齐次波动方程，它描述的是介质一经扰动后在区域里不再受到外力的运动规律；同时，若 u 关于空间位置仅随 x 方向变化，即 u=u(x,t) ，则方程为一维齐次波动方程。此时，拉普拉斯算子作用在 u 上的结果为：

给出一类一维齐次波动方程的定解问题，如下：

其中，方程（2）和（3）为定解条件。

利用微分算子改写上述一维齐次波动方程为：

若能找到两个新的微分算子，使其满足以下条件：

那么波动方程将被改写为：

此时，只需要将方程左右两边分别对 \xi 和 \eta 做两次积分，即可得到函数 u(\xi,\eta) ，再将 x,t 代入即可得到原方程的通解。

按照这个思路，假设 x 和 t 是关于 \xi 和 \eta 的函数：

根据多元复合函数的求导法则，分别写出关于 \xi 和 \eta 的微分算子：

要使式（4-3）成立，由于其中 A 和 B 均为常数系数，可任意设定，首先令 \frac{\partial t}{\partial \xi}=1,\frac{\partial x}{\partial \xi}=a ； \frac{\partial t}{\partial \eta}=-1,\frac{\partial x}{\partial \eta}=a ，在此条件下可使：

此时，

但是，为了后续书写的方便，我们重新令 \frac{\partial t}{\partial \xi}=\frac{1}{2a},\frac{\partial x}{\partial \xi}=\frac{1}{2} ； \frac{\partial t}{\partial \eta}=-\frac{1}{2a},\frac{\partial x}{\partial \eta}=\frac{1}{2} ，在此条件下可使：

将式（4-5）代入式（4-2）中波动方程，得到式（4-4）。首先对 \eta 求积分得：

其中， c(\xi) 为 \xi 的任意函数。再将上式对 \xi 求积分得：

由于 c(\xi) 为 \xi 的任意函数，所以积分的结果 f_{1}(\xi) 也为 \xi 的任意函数；另外 f_{2}(\eta) 也为 \eta 的任意函数。最后，将式（4-5）的变换代入上式，就得到了一维齐次波动方程的通解：

前面我们求得了一维齐次波动方程的通解，而达朗贝尔方程中的待求场量 A 和 \varphi 均是关于三维坐标 （x,y,z） 以及时间的函数，所以还需要研究三维空间中波动方程的求解问题。给出一类三维无界空间的自由振动问题，其描述如下：

其中， M 表示空间中任意一点 (x,y,z) 。考虑将三维空间的波动问题转化为一维齐次波动方程的求解——

以空间中任意一点 M_{0} 为球心，作半径为 r 的球面 S_{r}^{M_{0}} ：

定义函数：

\bar{u} 表示 u 在球面 S_{r}^{M_{0}} 上的平均值，由于某一确定球面上平均值 \bar{u} 处处相等，因此 \bar{u} 在空间位置上仅与球面半径 r 有关，同时 \bar{u} 还是关于时间的函数。需要补充的是，如果将求平均值的积分用球坐标表示， dS 如下图所示：

替换后得到式（4-7）最右侧的结果，其中 d\Omega 称为立体角元：

显然当所取球面的半径 r 趋近于零时，球面上的平均值 \bar{u} 就是点 M_{0} 处函数 u 的值，即：

根据以上思路，对式（4-6）中的波动方程两边在球面 S_{r}^{M_{0}} 上积分，并代入函数 \bar{u}(r,t) ，得：

交换微分与积分的顺序，得：

即

另外，对于方程右侧，需要计算在球坐标系下拉普拉斯算子的作用结果——

在直角坐标系下：

再根据图（4-1）中球面上一点在直角坐标系和球坐标系中的坐标之间的变换关系：

于是：

进一步：

类似地，得到：

于是，拉普拉斯算子作用在图（4-1）所示的球坐标系中的结果为：

而：

所以式（4-9）最终化简为：

至此，三维空间的波动问题被转化为一维齐次波动方程的求解——

式（4-8）变为：

其通解满足：

在上式第一个等式中，显然可得当 r=0 时：

因此，利用洛必达法则对 \bar{u} 取极限得到：

由式（4-10）可知， f^{'}_{1}(at)=f^{'}_{2}(-at) ，所以三维波动方程的通解为：

其中 f^{'}_{1}(at) 为任意函数。

设坐标原点处有一电荷量随时间变换的点电荷 q(t) ，除原点处外，点电荷所激发的标量位 \varphi 满足三维空间的齐次波动方程，根据式（3-5）：

由于点电荷 q(t) 激发的电场具有球对称性，电磁波以球面的形式向四周传播，所以在球坐标系中标量位 \varphi 仅是坐标 r 和时间 t 的函数，与坐标 \theta、\phi 无关，即 \varphi=\varphi(r,t) 。因此，可参考上一节对方程式（4-8）的求解，将式（4-11）转化为：

其中， v=1/\sqrt{\mu\varepsilon} 。

再根据一维齐次波动方程的求解方法，得到通解为：

其中， f_{1}(t-\frac{r}{v}) 和 f_{2}(t+\frac{r}{v}) 均为待定的函数，需要通过实际物理过程求得其定解。

下面根据实际的物理现象分析上述波动方程的定解——

从函数的数学形式可以看出： f_{1}(t-\frac{r}{v}) 是从原点出发，沿 +r 方向传播的行波，称为入射波； f_{2}(t+\frac{r}{v}) 是从原点出发，沿 -r 方向传播的行波，称为反射波。只有当电磁波在行进过程中遇到障碍时，才会出现反射波，此处考虑无限大均匀媒质中的电磁波，自然认为反射波不存在，因此取 f_{2}=0 。

另外，当点电荷 q 不随时间变换时，对应静电场的模型，此时标量位 \varphi 等于电位：

将方程的形式相对应，得到在变化的场源激励下，空间中标量位的分布为：

上式定解的形式根据实际的物理过程导出：

（1）若电荷量不随时间变化，上式与静电场中的电位分布相同。

（2）在场源点电荷的激发下，电磁波以速度 v 向周围传播。例如，在某一时刻 t_{0} ，某点 r_{0} 的标量位分子项大小为 q(t_{0}-\frac{r_{0}}{v}) ；经过 \Delta t 的时间，即 t_{0}+\Delta t 时刻，位置 r_{0}+v\Delta t 的标量位分子项大小为 q(t_{0}+\Delta t-\frac{r_{0}+v\Delta t}{v})=q(t_{0}-\frac{r_{0}}{v}) 即电磁波向前传播了距离 v\Delta t 。

利用叠加定理，空间体积 V^{'} 内的任意随时间变化的电荷分布 \rho(r^{'},t) 产生的标量位为：

其中， r 表示所求的场点 (x,y,z) ； r^{'} 表示激励源中的一点 (x^{'},y^{'},z^{'}) ， R=\left| r-r^{'} \right| 表示所求场点到场源中元电荷之间的距离。

对于标量位，在场源恒定时其等于静电场的电位函数；类似地，矢量位在场源恒定时等于恒定磁场的磁矢位。此处对恒定磁场中磁矢位的引入做一回顾——

由于恒定磁场时一个无散场，引入矢量函数 A 使得：

根据恒定磁场中的安培环路定理：

并且利用矢量恒等式：

得到：

再规定 A 的散度：

得到在此条件下矢量函数 A 满足的方程：

由于 A 是一个矢量场，在空间直角坐标系中，需要分别写出 x,y,z 三个方向上满足的方程：

即 A 在三个正交的方向上均满足泊松方程。

为了方便地求解以上泊松方程，需要类比静电场中的计算——在静电场中，根据：

可知电位 \varphi 满足泊松方程：

以空间中某一位置 r^{'} 处的点电荷 q 激发的电场为例，空间中电位满足上述泊松方程，而根据库仑定律求得的电位分布为：

其中 R=\left| r-r^{'} \right| 表示所求场点到场源（点电荷）之间的距离。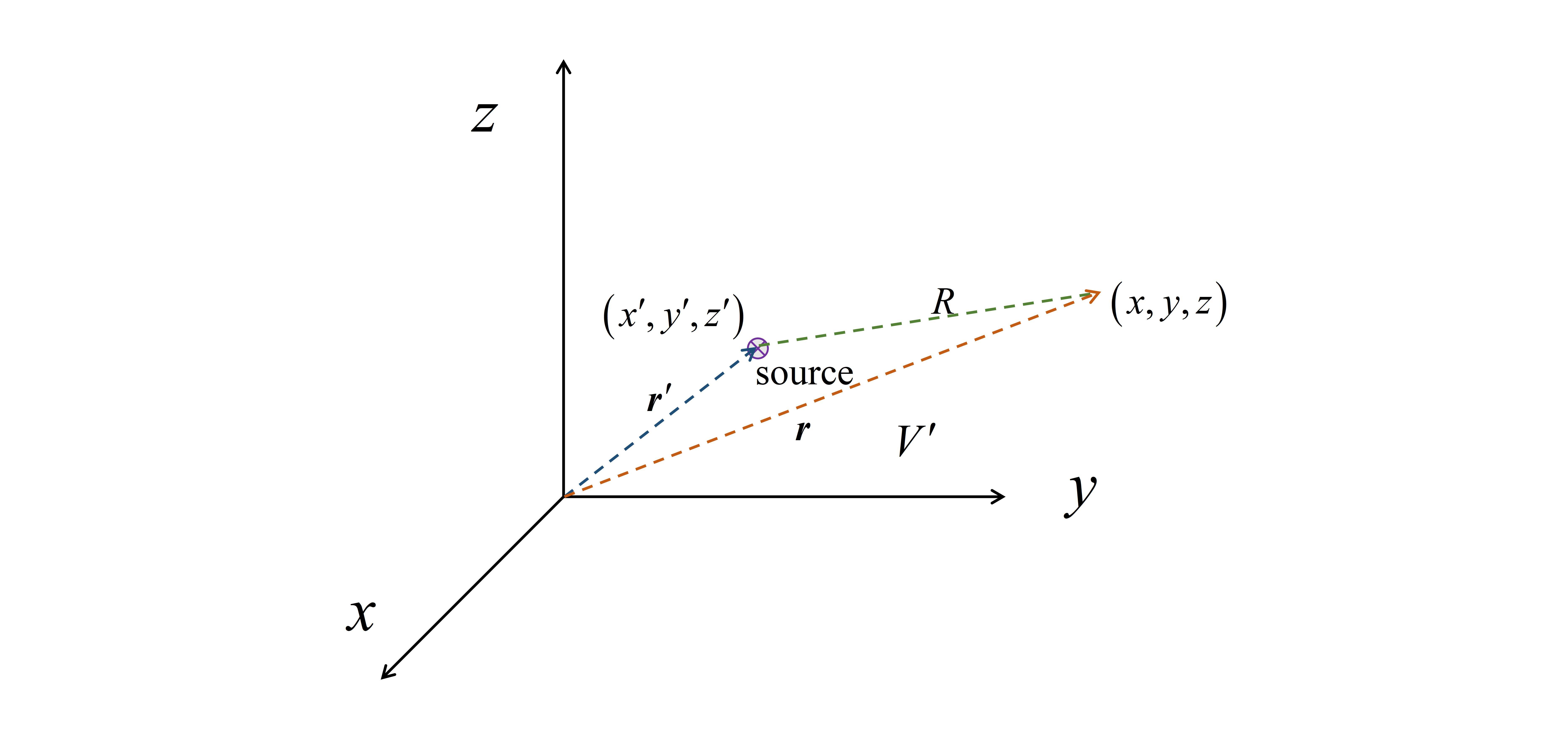

根据唯一性定理，泊松方程求解所得的电位分布必然与通过库仑定律计算的电位分布相同，这样就利用库仑定律导出了泊松方程解的形式。

另外，若静电场由空间体积 V^{'} 内的任意电荷分布 \rho(r^{'}) 产生，则利用库伦定律和叠加定理，积分求得空间中的电位分布：

至此，就得到了泊松方程的定解。

再利用上述推导的泊松方程解的形式，求解矢量场 A 满足的泊松方程：

空间体积 V^{'} 内的任意电流分布 J(r^{'}) 产生的磁矢位 A 为：

写成不同方向上标量形式为：

矢量形式与标量形式之间的关系为：

回到动态位的求解——

矢量函数 A 的达朗贝尔方程与标量函数 \varphi 的形式相同，因此具有相同的求解步骤。由于矢量位在场源恒定时等于恒定磁场的磁矢位，因此，定解的形式与式（4-12）相似。空间体积 V^{'} 内的任意电流分布 J(r^{'},t) 产生的矢量位为：

在时变电磁场中，主要研究正弦电磁场，其激励源和场量均以一定的频率按照正弦规律变化。复数表示法是研究正弦时变电磁场的有效工具。复数形式的正弦量包含其“幅值”和“相位”两个主要信息，并且复数表示法使得对时间的求导转化为了乘积运算，这些都有助于简化计算。

例如，在直角坐标系中有一随时间作正弦变化的电场强度 E ，它的瞬时值为：

用复数表示为：

复数形式与瞬时值之间的关系为：

复数形式和瞬时值对时间求导的关系为：

将正弦电磁场的激励源和场量均用复数形式表示，得到复数形式的达朗贝尔方程：

其中， \beta=\omega\sqrt{\mu\varepsilon} 被称为相位常数。下面求解复数形式的达朗贝尔方程——

与前文第三（c）节类似，仍然从原点处一变化的点电荷开始，由于此时电磁波以球面形式向外传播，标量位 \varphi 仅是坐标 r 和时间 t 的函数，与坐标 \theta、\phi 无关。因此，在除原点以外的空间之内，复数形式标量位的达朗贝尔方程可写为：

这可以看作一个二阶常系数齐次线性微分方程，其特征方程为 \lambda^{2}+\beta^{2}=0 ，特征方程的根为 \lambda_{1}=j\beta ， \lambda_{2}=-j\beta ，因此可以写出通解为：

复数形式的通解与瞬时值形式的通解相对应，例如分子项 C_{1}e^{-j\beta r} 对应 f_{1}(t-\frac{r}{v}) ，其中因子 e^{-j\beta r} 相当于相位推迟 \beta r=\omega\frac{r}{v} ，与前文分析的电磁波的传播特点一致。

至此，理解了复数形式的达朗贝尔方程，也就可以直接根据前文的瞬时值解写出复数形式的解：

求得动态位后再计算电场 E 和磁场 B ：

其中，电场 E 的计算应用了定义动态位时给出的矢量函数 A 的散度，即洛伦兹条件。可以看出，只要求得了矢量函数 A 就能得出空间中电磁场的分布。

单元偶极子天线是指一段载流细导线，它的长度 \Delta l 和横截面尺寸都比电磁波的波长以及观察点的距离小得多。因此，对于单元偶极子可忽略推迟效应，认为流过的电流是均匀且同向的；同时，任意场点到单元偶极子导线上各点的距离近似相同。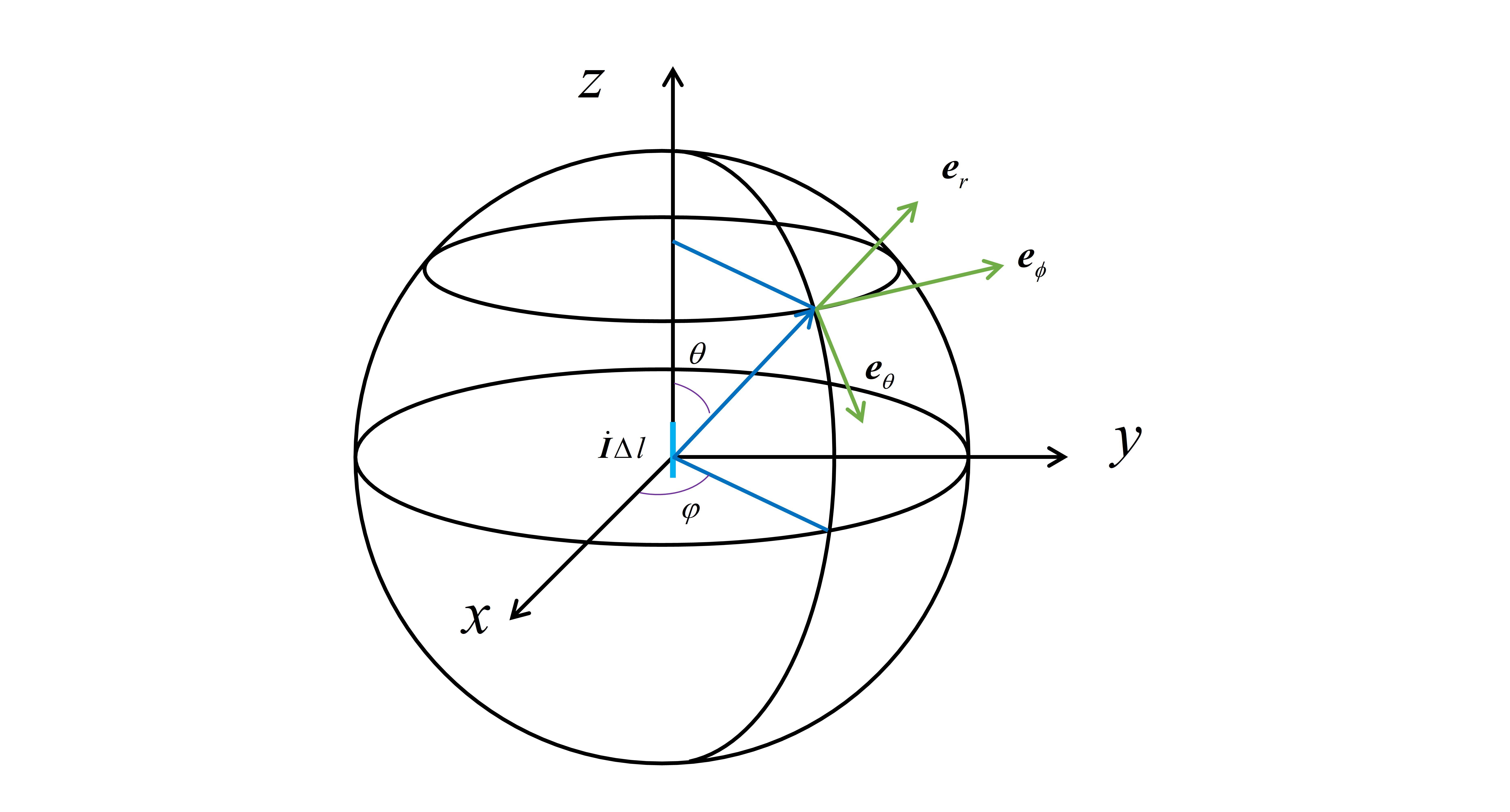

设图示单元偶极子上流过正弦电流 i(t)=I_{m}cos(\omega t+\phi) ，将其用复数表示，并求得空间中矢量位 A 的分布：

后续可以再由矢量位 A 求解空间中电磁场的分布，进一步分析天线电磁辐射的原理，内容参考《工程电磁场导论》（马西奎等）第四章。

后续来了：