| 矩阵的QR分解以及在最小二乘法中的应用 | 您所在的位置:网站首页 › 请用矩阵计算说明最小二乘法的方法 › 矩阵的QR分解以及在最小二乘法中的应用 |
矩阵的QR分解以及在最小二乘法中的应用
|
一、最小二乘法
最小二乘法是一种数学优化方法,通过最小化误差的平方和来拟合数据点。 以线性回归模型为例,如果我们用最小二乘法来求解线性回归的系数,可得: e r r ( y i − y ^ ) = 1 n ∑ i = 1 n ( y i − y ^ ) 2 = 1 n ∑ i = 1 n ( y i − w T x i ) 2 = 1 n ( y − w X ) T ( y − w X ) = 1 n ( y T y − 2 w X T y + w T X T X w ) \begin{aligned} err(y_i-\hat y) &= \frac{1}{n}\sum_{i=1}^n (y_i-\hat y)^2 = \frac{1}{n}\sum_{i=1}^n (y_i-w^Tx_i)^2\\ &= \frac{1}{n}(y-wX)^T(y-wX) \\ &= \frac{1}{n}(y^Ty-2wX^Ty+w^TX^TXw) \end{aligned} err(yi−y^)=n1i=1∑n(yi−y^)2=n1i=1∑n(yi−wTxi)2=n1(y−wX)T(y−wX)=n1(yTy−2wXTy+wTXTXw) 我们要求上式的最小值,要对其求导,然后寻找极小值点。 ∂ ∂ w e r r = 1 n ( 2 w X T X − 2 X T y ) = 0 w X T X = X T y w = ( X T X ) − 1 X T y \begin{aligned} \frac{\partial}{\partial w}err &= \frac{1}{n}(2wX^TX-2X^Ty) = 0\\ &wX^TX = X^Ty\\ &w=(X^TX)^{-1}X^Ty \end{aligned} ∂w∂err=n1(2wXTX−2XTy)=0wXTX=XTyw=(XTX)−1XTy 由此我们便可以推导出参数的表达式。 二、QR分解QR分解是把一个矩阵分解为一个正交矩阵和一个上三角矩阵的积。即有实数矩阵A,有 A = Q × R A=Q\times R A=Q×R,其中Q为正交矩阵( Q T ⋅ Q = I Q^T\cdot Q=I QT⋅Q=I),R为上三角矩阵。QR分解常见的算法有Gram–Schmid正交化、Household变换,以及Givens变换。 2.1 Gran-Schmid正交化设矩阵 A = ( a 1 ⃗ , a 2 ⃗ , . . . , a n ⃗ ) A=(\vec{a_1},\vec{a_2},...,\vec{a_n}) A=(a1 ,a2 ,...,an ),对矩阵A进行Gran-Schmid正交化过程。其中 p i ⃗ \vec{p_i} pi 为正交向量, q i ⃗ \vec{q_i} qi 为归一化后的标准正交向量, i = 1 , 2 , . . . , n i=1,2,...,n i=1,2,...,n 。 p 1 ⃗ = a 1 ⃗ = ∥ p 1 ⃗ ∥ q 1 ⃗ = r 11 q 1 ⃗ p 2 ⃗ = a 2 ⃗ − a 2 ⃗ ⋅ p 1 ⃗ ∥ p 1 ⃗ ∥ 2 ⋅ p 1 ⃗ = ∥ p 2 ⃗ ∥ q 2 ⃗ a 2 ⃗ = ∥ p 2 ⃗ ∥ q 2 ⃗ + a 2 ⃗ ⋅ p 1 ⃗ ∥ p 1 ⃗ ∥ 2 ⋅ p 1 ⃗ = ∥ p 2 ⃗ ∥ q 2 ⃗ + a 2 ⃗ ⋅ p 1 ⃗ ∥ p 1 ⃗ ∥ 2 ∥ p 1 ⃗ ∥ q 1 ⃗ = r 21 q 1 ⃗ + r 22 q 2 ⃗ p 3 ⃗ = a 3 ⃗ − a 3 ⃗ ⋅ p 1 ⃗ ∥ p 1 ⃗ ∥ 2 ⋅ p 1 ⃗ − a 3 ⃗ ⋅ p 2 ⃗ ∥ p 2 ⃗ ∥ 2 ⋅ p 2 ⃗ = ∥ p 3 ⃗ ∥ q 3 ⃗ a 3 ⃗ = ∥ p 3 ⃗ ∥ q 3 ⃗ + a 3 ⃗ ⋅ p 1 ⃗ ∥ p 1 ⃗ ∥ 2 ⋅ p 1 ⃗ + a 3 ⃗ ⋅ p 2 ⃗ ∥ p 2 ⃗ ∥ 2 ⋅ p 2 ⃗ = r 31 q 1 ⃗ + r 32 q 2 ⃗ + r 33 q 3 ⃗ \begin{aligned} \vec{p_1} &= \vec{a_1} = \lVert \vec{p_1}\rVert\vec{q_1}=r_{11}\vec{q_1}\\ \vec{p_2} &= \vec{a_2} - \frac{\vec{a_2}\cdot \vec{p_1}}{\lVert \vec{p_1}\rVert^2}\cdot \vec{p_1} = \lVert \vec{p_2}\rVert\vec{q_2}\\ \vec{a_2} &= \lVert \vec{p_2}\rVert\vec{q_2} + \frac{\vec{a_2}\cdot \vec{p_1}}{\lVert \vec{p_1}\rVert^2}\cdot \vec{p_1}\\ &= \lVert \vec{p_2}\rVert\vec{q_2} + \frac{\vec{a_2}\cdot \vec{p_1}}{\lVert \vec{p_1}\rVert^2}\lVert \vec{p_1}\rVert \vec{q_1}\\ &= r_{21}\vec{q_1} + r_{22}\vec{q_2}\\ \vec{p_3} &= \vec{a_3} - \frac{\vec{a_3}\cdot \vec{p_1}}{\lVert \vec{p_1}\rVert^2}\cdot \vec{p_1} - \frac{\vec{a_3}\cdot \vec{p_2}}{\lVert \vec{p_2}\rVert^2}\cdot \vec{p_2}\\ &= \lVert \vec{p_3}\rVert\vec{q_3}\\ \vec{a_3} &= \lVert \vec{p_3}\rVert\vec{q_3} + \frac{\vec{a_3}\cdot \vec{p_1}}{\lVert \vec{p_1}\rVert^2}\cdot \vec{p_1} + \frac{\vec{a_3}\cdot \vec{p_2}}{\lVert \vec{p_2}\rVert^2}\cdot \vec{p_2}\\ &= r_{31}\vec{q_1} + r_{32}\vec{q_2} + r_{33}\vec{q_3} \end{aligned} p1 p2 a2 p3 a3 =a1 =∥p1 ∥q1 =r11q1 =a2 −∥p1 ∥2a2 ⋅p1 ⋅p1 =∥p2 ∥q2 =∥p2 ∥q2 +∥p1 ∥2a2 ⋅p1 ⋅p1 =∥p2 ∥q2 +∥p1 ∥2a2 ⋅p1 ∥p1 ∥q1 =r21q1 +r22q2 =a3 −∥p1 ∥2a3 ⋅p1 ⋅p1 −∥p2 ∥2a3 ⋅p2 ⋅p2 =∥p3 ∥q3 =∥p3 ∥q3 +∥p1 ∥2a3 ⋅p1 ⋅p1 +∥p2 ∥2a3 ⋅p2 ⋅p2 =r31q1 +r32q2 +r33q3 之后通过分解矩阵 A A A: A = ( a 1 ⃗ , a 2 ⃗ , . . . , a n ⃗ ) = ( r 11 q 1 ⃗ , r 21 q 1 ⃗ + r 22 q 2 ⃗ , . . . , ∑ i = 1 n r n i q i ⃗ ) = ( r 11 q 1 ⃗ , r 21 q 1 ⃗ , r 31 q 1 ⃗ , . . . , r n 1 q 1 ⃗ ) + ( 0 , r 22 q 2 ⃗ , r 32 q 2 ⃗ , . . . , r n 2 q 2 ⃗ ) + . . . . . . + ( 0 , 0 , 0 , . . . , r n n q n ⃗ ) = ( q 1 ⃗ , q 2 ⃗ , . . . , q n ⃗ ) ⋅ [ r 11 r 21 ⋯ r n 1 0 r 22 ⋯ r n 2 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ r n n ] = Q ⋅ R \begin{aligned} A &= (\vec{a_1},\vec{a_2},... ,\vec{a_n})\\ &= (r_{11}\vec{q_1},r_{21}\vec{q_1}+r_{22}\vec{q_2},... ,\sum_{i=1}^n r_{ni}\vec{q_i})\\ &= (r_{11}\vec{q_1},r_{21}\vec{q_1},r_{31}\vec{q_1},...,r_{n1}\vec{q_1})\\ &+ (0,r_{22}\vec{q_2},r_{32}\vec{q_2},...,r_{n2}\vec{q_2})\\ &+...... \\ &+ (0,0,0,...,r_{nn}\vec{q_n})\\ &= (\vec{q_1},\vec{q_2},...,\vec{q_n})\cdot \left[ \begin{matrix} r_{11} & r_{21} & \cdots & r_{n1} \\ 0 & r_{22} & \cdots & r_{n2} \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & r_{nn} \\ \end{matrix} \right]\\ &=Q\cdot R \end{aligned} A=(a1 ,a2 ,...,an )=(r11q1 ,r21q1 +r22q2 ,...,i=1∑nrniqi )=(r11q1 ,r21q1 ,r31q1 ,...,rn1q1 )+(0,r22q2 ,r32q2 ,...,rn2q2 )+......+(0,0,0,...,rnnqn )=(q1 ,q2 ,...,qn )⋅⎣⎢⎢⎢⎡r110⋮0r21r22⋮0⋯⋯⋱⋯rn1rn2⋮rnn⎦⎥⎥⎥⎤=Q⋅R 2.2 Householder矩阵与Householder变换 设单位列向量 u ∈ R n u \in R^n u∈Rn,称 H = I − 2 u u T H=I-2uu^T H=I−2uuT为Householder矩阵(初等反射矩阵),由Householder矩阵所确定的线性变换( y = H x y=Hx y=Hx)称为Householder变换。 2.2.2 性质(1) H T = H H^T=H HT=H(实对称), H − 1 = H T H^{-1}=H^T H−1=HT(正交), H 2 = I H^2=I H2=I(对合), H − 1 = H H^{-1}=H H−1=H(自逆), d e t ( H ) = − 1 det(H)=-1 det(H)=−1 (2) 对于任何非零列向量 x ∈ R n x\in R^n x∈Rn及任何单位列向量 z ∈ R n z\in R^n z∈Rn,存在Householder矩阵 H H H,使得 H x = ∣ x ∣ z Hx=|x|z Hx=∣x∣z (3) 初等旋转矩阵(Givens矩阵)是两个初等反射矩阵 H H H的乘积 (定理证明请参照参考文献[2]) 2.2.3 采用Householder变换的QR分解A = [ b ( 1 ) ∗ ] A=\left[\begin{matrix} b^{(1)}& * \end{matrix}\right] A=[b(1)∗],存在 H 1 H_1 H1,使得 H 1 b ( 1 ) = ∣ b ( 1 ) ∣ e 1 → H 1 A = [ ∣ b ( 1 ) ∣ e 1 n A ( 1 ) ] H_1b^{(1)} =\left|b^{(1)}\right|e_1\to H_1A=\left[\begin{matrix}\left|b^{(1)}\right|e_1^nA^{(1)}\end{matrix}\right] H1b(1)=∣∣∣b(1)∣∣∣e1→H1A=[∣∣b(1)∣∣e1nA(1)] A ( 1 ) = [ b ( 2 ) ∗ ] A^{(1)}=\left[\begin{matrix} b^{(2)}& * \end{matrix}\right] A(1)=[b(2)∗],存在 H 2 H_2 H2,使得 H 2 A ( 1 ) = [ ∣ b ( 2 ) ∣ e 1 n − 1 A ( 2 ) ] L H_2A^{(1)} =\left[\begin{matrix}\left|b^{(2)}\right|e_1^{n-1}A^{(2)}\end{matrix}\right]L H2A(1)=[∣∣b(2)∣∣e1n−1A(2)]L A ( n − 2 ) = [ b ( n − 1 ) b ( n ) ] A^{(n-2)}=\left[\begin{matrix} b^{(n-1)}& b^{(n)} \end{matrix}\right] A(n−2)=[b(n−1)b(n)],存在 H n − 1 H_{n-1} Hn−1,使得 H n − 1 A ( n − 2 ) = [ a n − 1 , n − 1 ( n − 1 ) a n − 1 , n ( n − 1 ) 0 a n n ( n − 1 ) ] H_{n-1}A^{(n-2)} = \left[ \begin{matrix} a^{(n-1)}_{n-1,n-1} & a^{(n-1)}_{n-1,n}\\ \\ 0 & a_{nn}^{(n-1)} \end{matrix} \right] Hn−1A(n−2)=⎣⎢⎡an−1,n−1(n−1)0an−1,n(n−1)ann(n−1)⎦⎥⎤ 令 S = [ I n − 2 0 0 H n − 1 ] [ I n − 3 0 0 H n − 2 ] L [ I 2 0 0 H 3 ] [ 1 0 0 H 2 ] H 1 S=\left[ \begin{matrix} I_{n-2} & 0\\ \\ 0 & H_{n-1} \end{matrix} \right] \left[ \begin{matrix} I_{n-3} & 0\\ \\ 0 & H_{n-2} \end{matrix} \right]L \left[ \begin{matrix} I_{2} & 0\\ \\ 0 & H_{3} \end{matrix} \right] \left[ \begin{matrix} 1 & 0\\ \\ 0 & H_2 \end{matrix} \right] H_1 S=⎣⎡In−200Hn−1⎦⎤⎣⎡In−300Hn−2⎦⎤L⎣⎡I200H3⎦⎤⎣⎡100H2⎦⎤H1 H l + 1 = I n − l − 2 u u T ( u ∈ R n − 1 , u T u = 1 ) H_{l+1}=I_{n-l}-2uu^T(u\in R^{n-1},u^Tu=1) Hl+1=In−l−2uuT(u∈Rn−1,uTu=1) 则 [ I l 0 0 H l + 1 ] = [ I l 0 0 I n − l ] − 2 [ 0 0 0 u u T ] = I n − 2 [ 0 u ] [ 0 T u T ] = I n − 2 v v T \left[ \begin{matrix} I_l & 0\\ \\ 0 & H_{l+1} \end{matrix} \right]= \left[ \begin{matrix} I_l & 0\\ \\ 0 & I_{n-l} \end{matrix} \right]-2 \left[ \begin{matrix} 0 & 0\\ \\ 0 & uu^T \end{matrix} \right]= I_n-2\left[ \begin{matrix} 0\\ \\ u \end{matrix} \right] \left[ \begin{matrix} 0^T & u^T\\ \end{matrix} \right]=I_n-2vv^T ⎣⎡Il00Hl+1⎦⎤=⎣⎡Il00In−l⎦⎤−2⎣⎡000uuT⎦⎤=In−2⎣⎡0u⎦⎤[0TuT]=In−2vvT v T v = [ 0 T u T ] [ 0 u ] = u T u = 1 v^Tv= \left[ \begin{matrix} 0^T & u^T\\ \end{matrix} \right] \left[ \begin{matrix} 0\\ u \end{matrix} \right]=u^Tu=1 vTv=[0TuT][0u]=uTu=1 S A = [ a 11 ( 1 ) a 12 ( 1 ) L a 1 n ( 1 ) 0 a 22 ( 2 ) L a 2 n ( 2 ) 0 0 O M 0 0 0 a n n n − 1 ] = R , S − 1 = Q SA=\left[ \begin{matrix} a_{11}^{(1)} & a_{12}^{(1)} & L & a_{1n}^{(1)}\\ 0 & a_{22}^{(2)} & L & a_{2n}^{(2)}\\ 0 & 0 & O & M\\ 0 & 0 & 0 & a_{nn}^{n-1} \end{matrix} \right]=R,S^{-1}=Q SA=⎣⎢⎢⎡a11(1)000a12(1)a22(2)00LLO0a1n(1)a2n(2)Mannn−1⎦⎥⎥⎤=R,S−1=Q Q Q Q为正交矩阵 2.3 Givens矩阵与Givens变换 2.3.1 定义设实数 c c c与实数 s s s满足 c 2 + s 2 = 1 c^2+s^2=1 c2+s2=1,称 
为Givens矩阵,记作 T i j = T i j ( c , s ) T_{ij}=T_{ij}(c,s) Tij=Tij(c,s),由Givens矩阵确定的线性变换成为Givens变换(初等旋转变换)。 说明: (1).实数 c 2 + s 2 = 1 c^2+s^2=1 c2+s2=1,故存在 θ \theta θ,使 c = c o s θ , s = s i n θ c=cos\theta,s=sin\theta c=cosθ,s=sinθ (2). y = T i j x y=T_{ij}x y=Tijx中 T i j T_{ij} Tij确定了将向量变成 y y y的一种变换,正是Givens变换。二阶情况下, y = [ c o s θ s i n θ − s i n θ c o s θ ] x y=\left[\begin{matrix}cos\theta&sin\theta\\ -sin\theta&cos\theta\end{matrix}\right]x y=[cosθ−sinθsinθcosθ]x确定的正是平面直角坐标系中绕原点的一个旋转变换(旋转 θ \theta θ度)。 2.3.2 性质(1) [ T i j ( c , s ) ] − 1 = [ T i j ( c , s ) ] T = T i j ( c , − s ) [T_{ij}(c,s)]^{-1}=[T_{ij}(c,s)]^{T}=T_{ij}(c,-s) [Tij(c,s)]−1=[Tij(c,s)]T=Tij(c,−s), T i j T_{ij} Tij为正交矩阵。 d e t [ T i j ( c , s ) ] = 1 det[T_{ij}(c,s)]=1 det[Tij(c,s)]=1 (2) 设 x = [ a 1 , a 2 , ⋯ , a n ] T , y = T i j x = [ b 1 , b 2 , ⋯ , b n ] x=[a_1,a_2,\cdots,a_n]^T,y=T_{ij}x=[b_1,b_2,\cdots,b_n] x=[a1,a2,⋯,an]T,y=Tijx=[b1,b2,⋯,bn],则有, { b i = c × a i + s × a j b j = − s × a i + c × a j b k = a k , k ≠ i , j \begin{cases} b_i = c\times a_i+s\times a_j \\ b_j = -s\times a_i + c \times a_j\\ b_k=a_k,k\neq i,j \end{cases} ⎩⎪⎨⎪⎧bi=c×ai+s×ajbj=−s×ai+c×ajbk=ak,k=i,j (3) 设 x = [ a 1 , a 2 , ⋯ , a n ] T ≠ 0 x=[a_1,a_2,\cdots,a_n]^T\neq 0 x=[a1,a2,⋯,an]T=0,则存在有限个Givens矩阵的乘积T,使得 T x = ∣ x ∣ e 1 Tx=| x |e_1 Tx=∣x∣e1, 说明:(1). ∣ x ∣ = ∥ x ∥ 2 2 = x T x | x |=\sqrt{\lVert x \rVert_2^2}=\sqrt{x^Tx} ∣x∣=∥x∥22 =xTx (2). e 1 = [ 1 , 0 , 0 , ⋯ , 0 ] T e_1=[1,0,0,\cdots,0]^T e1=[1,0,0,⋯,0]T 推论:对于任何非零列向量 x ∈ R n x \in R^n x∈Rn及任何单位列向量 z ( ∣ z ∣ = 1 ) z(|z|=1) z(∣z∣=1),均存在着有限个Givens矩阵的乘积T,使 T x = ∣ x ∣ z Tx=| x |z Tx=∣x∣z (定理证明请参照参考文献[2]) 2.3.3 应用Givens旋转的QR分解可以用下面的这幅图来理解:x是没有改变的元素,m是改变了的元素。每一次箭头都进行了一次Givens旋转。  详细推导参见
矩阵QR分解 Givens变换 Household变换
2.4 总结
详细推导参见
矩阵QR分解 Givens变换 Household变换
2.4 总结
无论是Gram–Schmid正交化、Household变换,还是Givens变换,对矩阵进行QR分解的思路都是对矩阵进行多次线性变换,直至分解成一个正定矩阵与一个上三角矩阵的乘积。不同的方法有不同的优点和缺点。 三、最小二乘法中的QR分解已知线性回归的系数向量 w = ( X T X ) − 1 X T y w=(X^TX)^{-1}X^Ty w=(XTX)−1XTy,我们为什么不直接求解呢? 3.1 条件数计算机在进行运算的时候,有的时候会因为矩阵自身的特点而产生较大的误差。一个矩阵的条件数是它在计算机计算中的容易程度,条件数较大的时候矩阵计算就比较容易产生误差,此时该矩阵被称为病态矩阵。 条件数计算的公式为: c o n d i ( X ) = ∥ X − 1 ∥ ∥ X ∥ condi(X)=\lVert X^{-1}\rVert \lVert X\rVert condi(X)=∥X−1∥∥X∥ 若 ∥ ⋅ ∥ \lVert\cdot\rVert ∥⋅∥为2范数,则 c o n d i ( X ) = σ m a x ( X ) σ m i n ( X ) condi(X)=\frac{\sigma_{max}(X)}{\sigma_{min}(X)} condi(X)=σmin(X)σmax(X),其中 σ m a x ( X ) \sigma_{max}(X) σmax(X)与 σ m i n ( X ) \sigma_{min}(X) σmin(X)分别是矩阵 X X X的极大奇异值和极小奇异值(奇异值参考)。 若我们使用最小二乘法推导出的公式计算系数向量,我们可以看到 X T X X^TX XTX的条件数: c o n d i ( X T X ) = c o n d i ( V Σ T U T U Σ V H ) = c o n d i ( V Σ 2 V H ) = c o n d i ( X ) 2 condi(X^TX)=condi(V\Sigma^TU^TU\Sigma V^H)=condi(V\Sigma ^2V^H)=condi(X)^2 condi(XTX)=condi(VΣTUTUΣVH)=condi(VΣ2VH)=condi(X)2 然而通过使用QR分解,我们可以将条件数降到尽量低。 3.2 最小二乘法与QR分解我们首先将训练集 X X X分解为 X = Q R X=QR X=QR,再带入上面计算系数矩阵的公式中。 w ^ ∗ = ( X T X ) − 1 X T y X T X w ^ ∗ = X T y R T Q T Q R w ^ ∗ = R T Q T y R T R w ^ ∗ = R T Q T y ( Q T Q = I ) R w ^ ∗ = Q T y w ^ ∗ = R − 1 Q T y \begin{aligned} \hat w^* &= (X^TX)^{-1}X^Ty \\ X^TX\hat w^* &= X^Ty \\ R^TQ^TQR\hat w^*&= R^TQ^Ty \\ R^TR\hat w^*&= R^TQ^Ty(Q^TQ=I) \\ R\hat w^*&= Q^Ty \\ \hat w^*&= R^{-1}Q^Ty \end{aligned} w^∗XTXw^∗RTQTQRw^∗RTRw^∗Rw^∗w^∗=(XTX)−1XTy=XTy=RTQTy=RTQTy(QTQ=I)=QTy=R−1QTy 我们仅需直到X的QR分解就可以直接计算出 w w w。 四、参考文献[1]. 用QR分解求最小二乘法的最优闭式解 [2]. 矩阵QR分解 Givens变换 Household变换 [3]. 矩阵的QR分解 [4]. QR decomposition and Givens Rotation [4]. QR分解与最小二乘 [5]. QR分解之Household变换 [6]. 矩阵论基础知识 |
【本文地址】
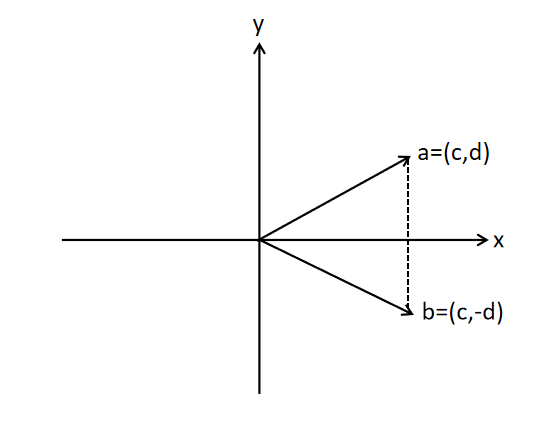 在平面直角坐标系中,将向量
a
⃗
=
(
c
,
d
)
\vec a=(c,d)
a
=(c,d)作关于x轴的交换,可得到:
b
=
[
c
−
d
]
=
[
1
0
0
−
1
]
[
c
d
]
=
(
I
−
2
[
0
1
]
[
0
1
]
T
)
x
=
H
x
b = \left[ \begin{matrix} c\\-d \end{matrix} \right]=\left[ \begin{matrix} 1 & 0\\ 0 & -1 \end{matrix}\right] \left[ \begin{matrix} c\\ d \end{matrix} \right]=(I-2 \left[ \begin{matrix} 0\\ 1 \end{matrix} \right] \left[ \begin{matrix} 0\\ 1 \end{matrix} \right]^T)x=Hx
b=[c−d]=[100−1][cd]=(I−2[01][01]T)x=Hx 可将其推广至:
在平面直角坐标系中,将向量
a
⃗
=
(
c
,
d
)
\vec a=(c,d)
a
=(c,d)作关于x轴的交换,可得到:
b
=
[
c
−
d
]
=
[
1
0
0
−
1
]
[
c
d
]
=
(
I
−
2
[
0
1
]
[
0
1
]
T
)
x
=
H
x
b = \left[ \begin{matrix} c\\-d \end{matrix} \right]=\left[ \begin{matrix} 1 & 0\\ 0 & -1 \end{matrix}\right] \left[ \begin{matrix} c\\ d \end{matrix} \right]=(I-2 \left[ \begin{matrix} 0\\ 1 \end{matrix} \right] \left[ \begin{matrix} 0\\ 1 \end{matrix} \right]^T)x=Hx
b=[c−d]=[100−1][cd]=(I−2[01][01]T)x=Hx 可将其推广至: