| 复变函数:傅里叶变换 | 您所在的位置:网站首页 › 解析是什么意思复变函数 › 复变函数:傅里叶变换 |
复变函数:傅里叶变换
|
傅里叶级数针对周期函数,为了可以处理非周期函数,需要傅里叶变换。关于傅里叶级数的内容参见傅里叶级数 1 傅里叶级数 1.1 傅里叶级数是向量从代数上看,傅里叶级数就是通过三角函数和常数项来叠加逼近周期为T的函数
f
(
x
)
f(x)
f(x): 在上面的示例函数中增加几个三角函数: 0 H z ⟺ s i n ( 0 x ) 3 H z ⟺ s i n ( 3 x ) ⋯ 0Hz\iff sin(0x)\quad3Hz\iff sin(3x)\cdots 0Hz⟺sin(0x)3Hz⟺sin(3x)⋯ 高度则代表在这个频率上的振幅,也就是这个基上的坐标分量。 这里举的例子只有正弦函数,余弦函数其实也需要这样一个频谱图,也就是需要两个频谱图,此外还有一种结合正弦和余弦的方式,这个放在后面。 原来的曲线图就称为时域图,往往把时域图和频域图画在一起,这样才能较为完整的反映傅里叶级数。 当习惯了频域后,再看频域图似乎就看到了傅里叶级数的展开:
以上关于傅里叶级数的说明都是基于周期函数,假如有如下一个非周期函数,那么傅里叶级数该怎么处理?
在这样的思路下,就可以使用三角级数来逼近这个函数 观察下频域,对于周期为T的函数 f ( x ) f(x) f(x),其基为: { 1 , c o s ( 2 π n T x ) , s i n ( 2 π n T x ) } \{1,cos(\frac{2\pi n}{T}x),sin(\frac{2\pi n}{T}x)\} {1,cos(T2πnx),sin(T2πnx)} 刚才举例的方波
T
=
2
π
T=2\pi
T=2π,对应的基就为(没有余弦波): 傅里叶级数是: f ( x ) = ∑ n = − ∞ ∞ c n ⋅ e i 2 π n x T ( T = ∞ ) ⟹ f ( x ) = ∫ − ∞ ∞ F ( w ) e i w x d w f(x)=\sum\limits_{n=-\infty}^{\infty}c_n\cdot e^{i\frac{2\pi nx}{T}}(T=\infty)\Longrightarrow f(x)=\int_{-\infty}^{\infty}F(w)e^{iwx}dw f(x)=n=−∞∑∞cn⋅eiT2πnx(T=∞)⟹f(x)=∫−∞∞F(w)eiwxdw 上面进行了一些简化,用 w w w代表频率。(?) 其中 F ( w ) F(w) F(w)得到的过程如下所示: c n = 1 T ∫ x 0 x 0 + T f ( x ) ⋅ e − i 2 π n x T d x ( T = ∞ ) ⟹ F ( w ) = 1 2 π ∫ − ∞ ∞ f ( x ) e − i w x d x c_n=\frac{1}{T}\int_{x_0}^{x_0+T}f(x)\cdot e^{-i\frac{2\pi nx}{T}dx}(T=\infty)\ \Longrightarrow F(w)=\frac{1}{2\pi}\int_{-\infty}^{\infty}f(x)e^{-iwx}dx cn=T1∫x0x0+Tf(x)⋅e−iT2πnxdx(T=∞) ⟹F(w)=2π1∫−∞∞f(x)e−iwxdx F ( w ) F(w) F(w)就是傅里叶变换,得到的就是频域曲线。 下面两者称为傅里叶变换对,可以相互转换: f ( x ) ⟺ F ( w ) f(x)\iff F(w) f(x)⟺F(w) 正如之前所说的,这是看待同一个数学对象的两种形式,一个是函数,一个是向量。 https://www.matongxue.com/madocs/712.html |
【本文地址】
 这一过过程,实际上是把
f
(
x
)
f(x)
f(x)当作了如下基的向量:
这一过过程,实际上是把
f
(
x
)
f(x)
f(x)当作了如下基的向量: 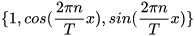 那么上面的式子就可以解读为:
那么上面的式子就可以解读为:  以一个例子来说明,比如一个
T
=
2
π
T=2\pi
T=2π的方波
f
(
x
)
f(x)
f(x),可以粗略的写作
f
(
x
)
≈
1
+
4
π
s
i
n
(
x
)
f(x)\approx1+{4\over\pi}sin(x)
f(x)≈1+π4sin(x)
以一个例子来说明,比如一个
T
=
2
π
T=2\pi
T=2π的方波
f
(
x
)
f(x)
f(x),可以粗略的写作
f
(
x
)
≈
1
+
4
π
s
i
n
(
x
)
f(x)\approx1+{4\over\pi}sin(x)
f(x)≈1+π4sin(x) 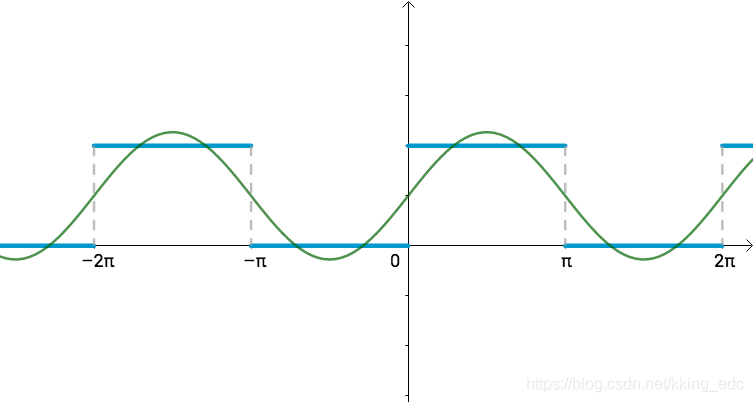 我们可以认为上面函数的基为
{
1
,
s
i
n
(
x
)
}
\{1,sin(x)\}
{1,sin(x)},则
f
(
x
)
f(x)
f(x)相当于向量
(
1
,
4
π
)
(1,{4\over\pi})
(1,π4),画到图上如下(注意横纵坐标不是
x
,
y
x,y
x,y,而是
1
,
s
i
n
(
x
)
)
1,sin(x))
1,sin(x)):
我们可以认为上面函数的基为
{
1
,
s
i
n
(
x
)
}
\{1,sin(x)\}
{1,sin(x)},则
f
(
x
)
f(x)
f(x)相当于向量
(
1
,
4
π
)
(1,{4\over\pi})
(1,π4),画到图上如下(注意横纵坐标不是
x
,
y
x,y
x,y,而是
1
,
s
i
n
(
x
)
)
1,sin(x))
1,sin(x)): 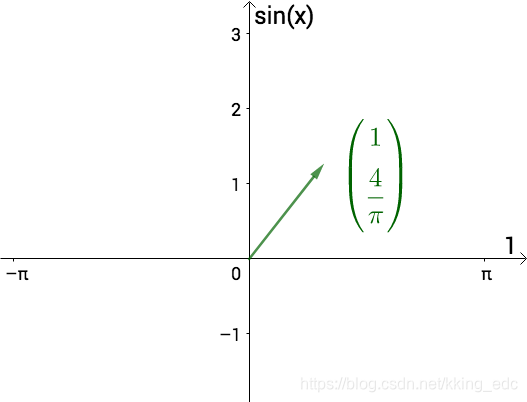
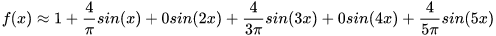 此时从几何上来看,图像更为接近:
此时从几何上来看,图像更为接近: 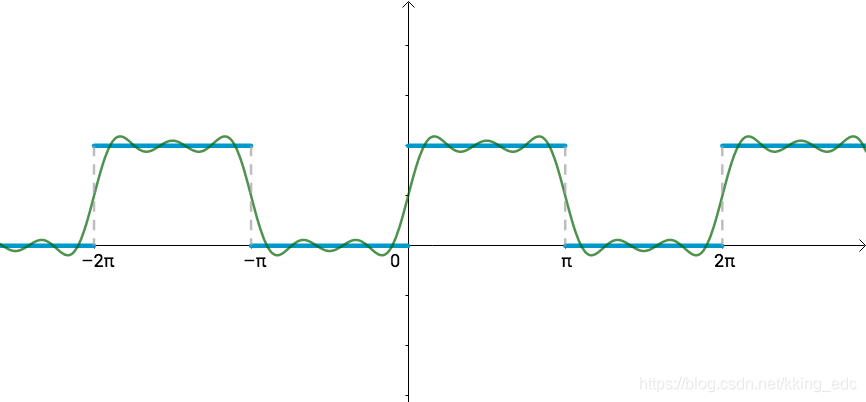 这时的基为:
这时的基为: 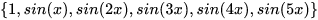 对应的向量为:
对应的向量为: 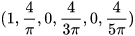 六维的向量我们是没有办法通过坐标图来表示的,因此数学家使用了一个频域图来表示这个向量:
六维的向量我们是没有办法通过坐标图来表示的,因此数学家使用了一个频域图来表示这个向量: 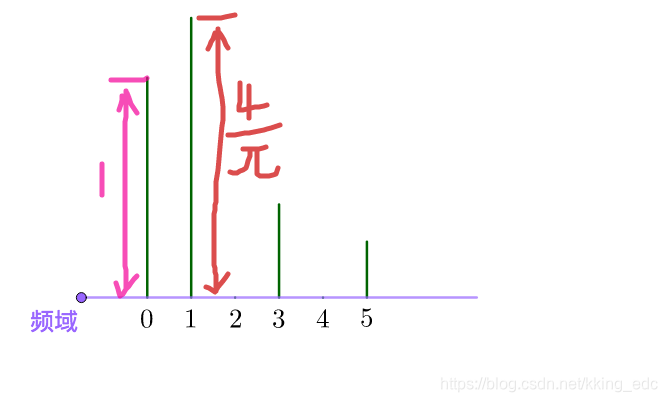 上图中的0,1,2,3,4,5分别代表了不同频率的正弦波函数,也就是之前的基:
上图中的0,1,2,3,4,5分别代表了不同频率的正弦波函数,也就是之前的基: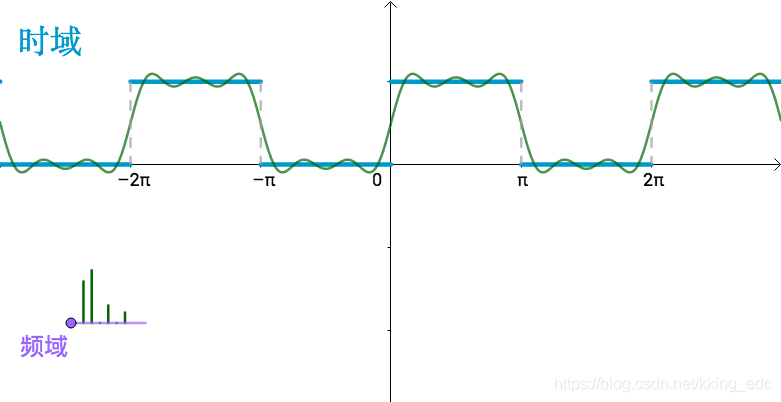 不管是时域还是频域,其实反映的都是同一个直线,只不过一个用了函数的观点,而另一个用了向量的观点。
不管是时域还是频域,其实反映的都是同一个直线,只不过一个用了函数的观点,而另一个用了向量的观点。
 我们可以变换一下思路,如果刚才方波的周期:
T
=
2
π
→
T
=
∞
T=2\pi\to T=\infin
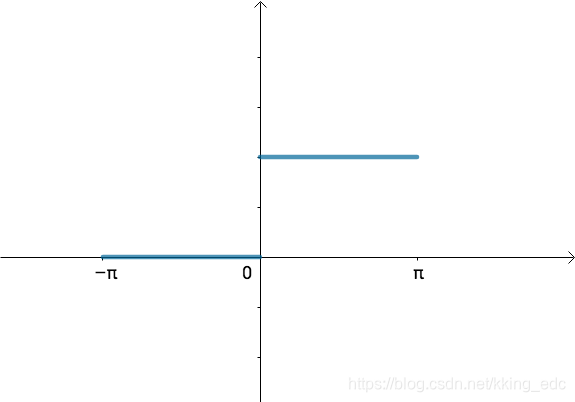
T=2π→T=∞ 那么可以得到一个如下的函数:
我们可以变换一下思路,如果刚才方波的周期:
T
=
2
π
→
T
=
∞
T=2\pi\to T=\infin
T=2π→T=∞ 那么可以得到一个如下的函数:

 对应的频率就是:
对应的频率就是: 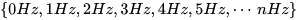 按照刚才的思路,如果T不断变大,比如让
T
=
4
π
T=4\pi
T=4π,对应的基就为(没有余弦波):
按照刚才的思路,如果T不断变大,比如让
T
=
4
π
T=4\pi
T=4π,对应的基就为(没有余弦波):  对应的频率就为:
对应的频率就为: 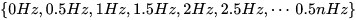 和刚才相比,频率更加密集
和刚才相比,频率更加密集  之前方波的频域图,画了前五十个频率,可以看到随着
T
T
T不断变大,这50个频率越来越集中:
之前方波的频域图,画了前五十个频率,可以看到随着
T
T
T不断变大,这50个频率越来越集中: 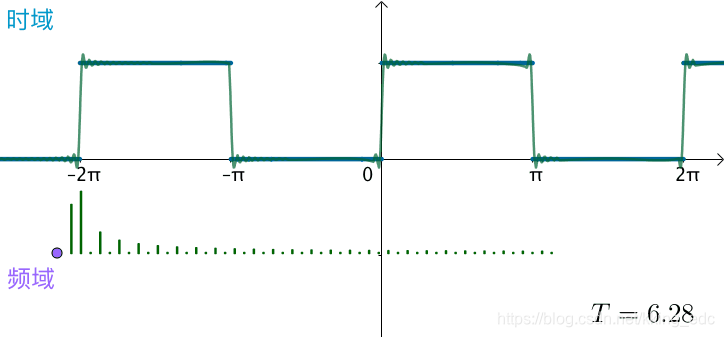
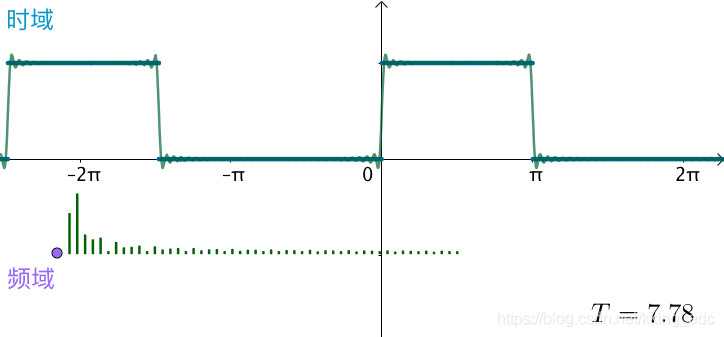
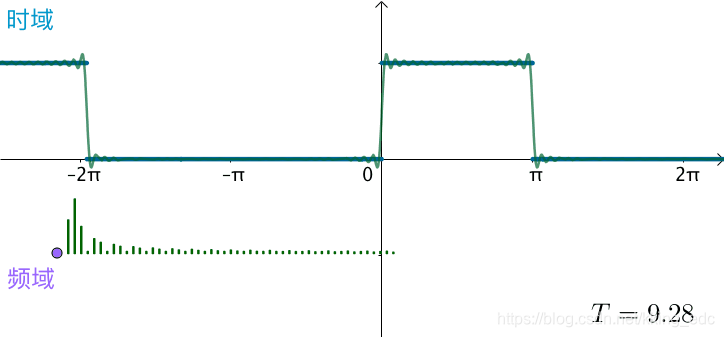
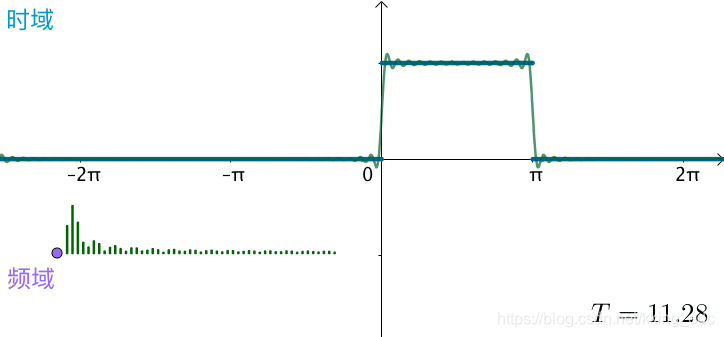 可以想象,如果真的:
T
=
2
π
→
T
=
∞
T=2\pi\to T=\infty
T=2π→T=∞,这些频率就会变得稠密,直至连续,变为一条频域曲线:
可以想象,如果真的:
T
=
2
π
→
T
=
∞
T=2\pi\to T=\infty
T=2π→T=∞,这些频率就会变得稠密,直至连续,变为一条频域曲线: 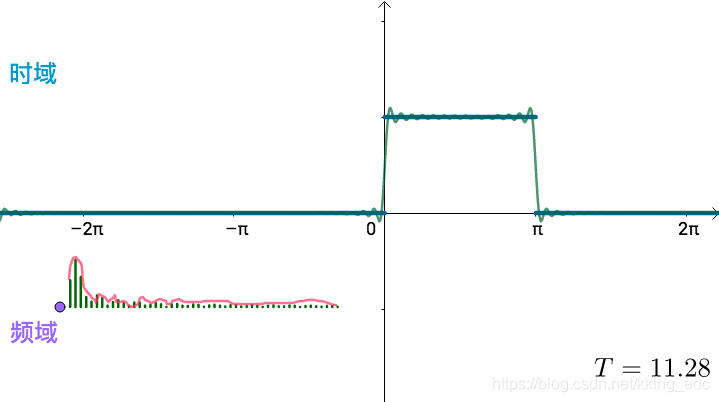 傅里叶变换就是,让
T
=
∞
T=\infty
T=∞,求出上面这根频域曲线。
傅里叶变换就是,让
T
=
∞
T=\infty
T=∞,求出上面这根频域曲线。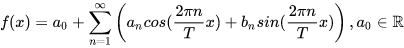 这里有正弦波和余弦波,画频域图不方便,通过欧拉公式,可以转变为复数形式:
这里有正弦波和余弦波,画频域图不方便,通过欧拉公式,可以转变为复数形式: 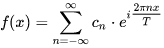 其中:
其中: 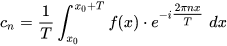 复数形式也是向量,可以理解为:
复数形式也是向量,可以理解为: 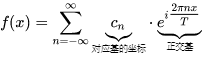 只不过这里
c
n
c_n
cn是复数,不好画频域图,当周期推向无穷的时候可以得到:
只不过这里
c
n
c_n
cn是复数,不好画频域图,当周期推向无穷的时候可以得到: