模糊C均值聚类（Fuzzy C

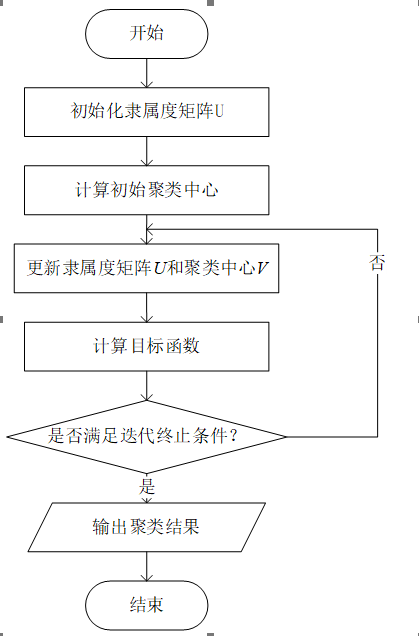
本文的代码与数据地址已上传至github：https://github.com/helloWorldchn/MachineLearning

L.A.Zadeh在1965年的“Information and Control”期刊中最早提出模糊集理论，原始文献为“Fuzzy sets”。在该理论中，针对传统的硬聚类算法其隶属度值非0即1的严格隶属关系，使用模糊集合理论，将原隶属度扩展为 0 到 1 之间的任意值，一个样本可以以不同的隶属度属于不同的簇集，从而极大提高了聚类算法对现实数据集的处理能力，由此模糊聚类出现在人们的视野。FCM算法广泛应用在数据挖掘、机器学习和计算机视觉与图像处理等方向。

模糊C均值聚类（Fuzzy C-means）算法简称FCM算法，是软聚类方法的一种。FCM算法最早由Dunn在1974年的期刊“Journal of Cybernetics”文献中提出，文献为“A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clusters”，然后在1984年经 Bezdek于“Computers & Geosciences”推广，原始文献为“FCM: The fuzzy c-means clustering algorithm”。

硬聚类算法在分类时有一个硬性标准，根据该标准进行划分，分类结果非此即彼。 软聚类算法更看重隶属度，隶属度在[0,1]之间，每个对象都有属于每个类的隶属度，并且所有隶属度之和为 1，即更接近于哪一方，隶属度越高，其相似度越高。

模糊 C-均值聚类（FCM）算法一种软聚类的聚类方法，该方法的思想使用 隶属度来表示每个数据之间的关系，从而确定每个数据点属于的聚类簇的聚类方法。同时 FCM 算法也是一种基于目标函数的算法，给定含有n个数据的数据集： X = { x 1 , x 2 , … x i , … , x n } X=\left\{\right.x_1,x_2,…x_i,…,x_n\left\}\right. X={x1​,x2​,…xi​,…,xn​}， X i X_i Xi​是第 i i i个特征向量; X i j X_{ij} Xij​是 X i Xi Xi的第 j j j个属性。每个样本包含 d d d个属性。FCM算法可以将该数据集划分为 K K K类， K K K为大于1的正整数，其中 K K K个类的聚类中心分别为 [ v 1 , v 2 , … , v n ] [v_1,v _2,…,v_n] [v1​,v2​,…,vn​]。 FCM的目标函数和约束条件如下：

J ( U , V ) = ∑ i = 1 n ∑ j = 1 k u i j m d i j 2 J(U,V)=\displaystyle\sum_{i=1}^{n} \displaystyle\sum_{j=1}^{k} u_{ij}^md_{ij}^2 J(U,V)=i=1∑n​j=1∑k​uijm​dij2​

∑ j = 1 k u i j = 1 , u i j ∈ [ 0 , 1 ] \displaystyle\sum_{j=1}^{k} u_{ij}=1, u_{ij}∈[0,1] j=1∑k​uij​=1,uij​∈[0,1]

其中， u i j u_{ij} uij​是样本点 x i x_i xi​与聚类中心 v j v_j vj​的隶属度，m是模糊指数（m>1）， d i j d_{ij} dij​是样本点 x i x_i xi​与聚类中心 v j v_j vj​的距离，一般采用欧氏距离。聚类即是求目标函数在约束条件的最小值。FCM 算法通过对目标函数的迭代优化来取得对样本集的模糊分类。

为使目标函数 J 取得最小值，在满足约束条件的情况下对目标函数使用拉格朗日（Lagrange）乘数法，得到隶属度矩阵U和聚类中心 v j v_j vj​。

u i j = 1 ∑ c = 1 k ( d i j d i k ) 2 m − 1 u_{ij}=\frac{1}{\displaystyle\sum_{c=1}^{k} (\frac{d_{ij}}{d_{ik}}) ^\frac{2}{m-1}} uij​=c=1∑k​(dik​dij​​)m−12​1​

v j = ∑ i = 1 n u i j m x i ∑ i = 1 n u i j m v_j=\frac{\displaystyle\sum_{i=1}^{n} u_{ij}^m x_i }{\displaystyle\sum_{i=1}^{n} u_{ij}^m } vj​=i=1∑n​uijm​i=1∑n​uijm​xi​​

算法的具体描述如下：

输入：聚类数目c，数据集 X = { x 1 , x 2 , … x i , … , x n } X=\left\{\right.x_1,x_2,…x_i,…,x_n\left\}\right. X={x1​,x2​,…xi​,…,xn​}，停止阈值ε，模糊因子m，最大迭代次数T； 输出：聚类中心 V = [ v 1 , v 2 , … , v c ] V=[v_1,v _2,…,v_c] V=[v1​,v2​,…,vc​], 隶属度矩阵U； Step1：设置聚类数目c； Step2：初始化模糊因子m、迭代允许的误差ε、迭代次数t=0和隶属度矩阵U(0)，从样本中随机选取c个样本作为初始聚类中心； Step3：根据公计算或更新隶属度矩阵U，并更新聚类中心； Step4：比较 J ( t ) J(t) J(t)和 J ( t − 1 ) J{(t-1)} J(t−1) ；若 ∣ ∣ J t − J ( t − 1 ) ∣ ∣ ≤ ε || J{t} - J{(t-1)} || ≤ ε ∣∣Jt−J(t−1)∣∣≤ε，则满足迭代停止条件，迭代停止。否则置 t = t + 1 t=t+1 t=t+1，返回Step3，继续迭代。

FCM流程图如下：

输入：聚类数目c，数据集 X = { x 1 , x 2 , … x i , … , x n } X=\left\{\right.x_1,x_2,…x_i,…,x_n\left\}\right. X={x1​,x2​,…xi​,…,xn​}，停止阈值ε，模糊因子m，最大迭代次数T； 输出：聚类中心 V = [ v 1 , v 2 , … , v c ] V=[v_1,v _2,…,v_c] V=[v1​,v2​,…,vc​], 隶属度矩阵U；

在有n个样本的d维数据集X中，数据集被划分成c个簇，如果本次聚类经过了t次迭代，每次迭代需要计算一次目标函数，计算过程中需要分别求出d维数据中c个簇的聚类中心与n个数据的距离，算法在此过程的时间复杂度为O(n∙c∙d)。隶属度矩阵需要计算c次距离，所以每轮迭代需要的时间复杂度为O(n∙c2d)。综上所述模糊C均值算法的时间复杂度为O(n∙c2∙t∙d)。但是由于在一般情况下类簇数目c、数据维度d以及算法的迭代次数t均可认为是常量，所以模糊C均值算法的时间复杂度可以简化为O(n)。由此可见，模糊C均值算法的时间复杂度随着数据点的数量增加呈线性增长，同时也受迭代次数、聚类簇数目以及数据维度的影响。

FCM算法的核心步骤就是通过不断地迭代，更新聚类簇中心，达到簇内距离最小。算法的时间复杂度很低，因此该算法得到了广泛应用，但是该算法存在着许多不足，算法主要优缺点如下：

FCM算法优点：

FCM算法缺点：

本文使用的数据集为UCI数据集，分别使用鸢尾花数据集Iris、葡萄酒数据集Wine、小麦种子数据集seeds进行测试，本文从UCI官网上将这三个数据集下载下来，并放入和python文件同一个文件夹内即可。同时由于程序需要，将数据集的列的位置做出了略微改动。数据集具体信息如下表：

数据集在我主页资源里有，免积分下载，如果无法下载，可以私信我。