| 对于p值(p | 您所在的位置:网站首页 › 统计学中p值的意义 › 对于p值(p |
对于p值(p
|
在正文前,觉得有必要先做一点说明,写这篇文章的初衷是帮助理解概念,因而在对概念的定义和外延做简化的时候严谨度很难避免会有所降低,如有谬误之处也请海涵和提出交流,非常欢迎交流想法。 所谓显著性水平,可以认为是一个临界水平,我们拿某次实验得到的实际的p-value与该显著性水平下理论上应该是多少的p-value的临界值进行比较。如果实际的p-value比临界值上的p-value低,则说明结果显著,如果实际的p-value比临界值上的p-value高,则说明结果不显著。在很多统计分析软件里,在做完某项检验后除了输出检验统计量的值,还会输出sig,这个sig就是p-value,比如用SPSS执行的一次F检验。 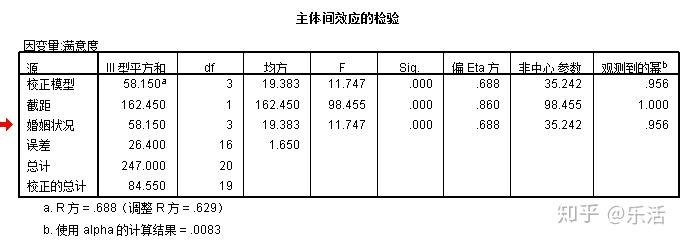 在检验表的下方有标注:使用alpha的计算结果=.0083,即表示在显著性水平设定为0.0083时,p-value的临界值便是0.0083,检验中得到的sig因为比显著性水平下的临界值低,因此结果显著,拒绝了原假设。F检验的原假设是不同组之间的平均值u1=u2=u3=...=un,原假设被拒绝即表示各组之间的平均值有显著的差异。 因此统计当中的”结果显著”可以翻译成是得到了与原定假设中显著不同的结论,意味着原假设被推翻。最早提出p-value概念的Fisher曾对p-value的应用范围有这样的解释:“...知道如何设计一个试验,而这个试验几乎一定能给出一个显著性的结果。”这句话是Fisher使用显著性检验的核心所在,他认为研究者必须先要对自己的研究设计有一个成熟的认知,把试验的各个环节设计得非常科学严谨后,显著性检验才有意义。如果实验设计本身出了问题,那么显著性检验的结果必然也会把人引向歧途。根据他的那段论述,显著性检验在推翻原假设上,说服力是非常强的,这就好比我们解数学题时要证明一个说法错误,只要列举一个反例就能够做到。然而,要证明一个定理的正确,则需要将全部可能的情况分类讨论,论证它在各种条件下能否适用,难度无疑比起前者大了很多。同样的道理,显著性检验如果结果显著,表示在原假设下出现了特例,反之,如果结果不显著,也不能证明原假设是正确的,只能够得出这样的结论:不能拒绝原假设(拒绝原假设的证据不够充分,但不意味着没有。你做假设检验的这份样本里无法得出拒绝原假设的结论,不意味着其他样本里没有这样的特例~) 所以Fisher指出显著性检验可能得出的三种结论: 一. p-value很小(通常是小于0.01),他认为某种结果已经确实无疑地表现出来了,也就是说基本能够否定原假设了。 二. p-value很大(通常大于0.2),他宣称即使这个结果真的存在,也会因为该结果发生的可能性太小,所以不可能有任何能够显示出这个结果的大规模实验。其大意就是因为p-value不显著,即使真实的情况是原假设是错误的,也会因为这种情况发生的几率太小,使得在实际中没办法做那么大样本的实验来支持这一论点。 三.p-value介于二者之间,Fisher则讨论了应如何设计下一个实验,才能够优化自己的结果。 事实上,很多做显著性检验的步骤都是先假定样本数据服从某一分布,将其作为原假设进行检验。再从结果是否显著来判断样本的分布形态是否是事先假设的那个分布形态。因为分布形态有可能会受到自由度跟样本数量的影响,所以在不同的显著性检验里p-value的检验值是不一样的。那么一个问题就出来了,用什么标准来衡量不同自由度和样本量下的结果是否显著,于是随着进一步探索,就出现了统计教材上经常可以查到的那个p-value检验表。 J.奈曼进一步提出,显著性检验必须要伴随有至少两个可能的假设,否则显著性检验根本没有任何意义。也就是我们现在所说的一项检验里需要包含原假设与备择假设,比如要检验一组数据是否服从正态分布,那么一项假设是它服从正态分布,另一项假设是它服从正态分布以外其他的分布(也就是原假设的补集),奈曼在此基础上提出备择假设不能太多,原因很简单:如果结果显著的话,原假设被推翻,接受备择假设,备择假设中包含的可能情况实在太多了,譬如上面举的那个例子,除了正态分布以外有那么多分布,做了这个实验我还是不知道样本属于哪一种分布形态,那么我得出这个结论的意义有多大呢?在设计实验时,这个问题是很容易被忽略的。 有时也会把p-value的值解释为在实验里犯第一类错误的概率(原假设为真却由显著性检验得到拒绝原假设的结论),为了便于理解,以正态曲线为例(徒手画的,画的不好请见谅):  例如一次抽样,实验中将显著性水平设定为0.05,如果样本服从正态分布的话,则在上面这个由样本点组成的图中,检验的临界值(也就是平均值两个标准差)以内应涵盖95%的样本点,检验的临界值以外应涵盖5%的样本点,p-value则等于观测的样本点在这两个标准差以外出现的概率。比如观测的样本是100个,如果这个样本服从正态分布的话,应该95个样本点在均值的2个标准差以内,有5个样本点会落到均值的2个样本点以外,但是如果实际情况是10个样本点落到了均值的两个样本点以外的话,p-value=在正态分布下100个总体中,10个样本点落到临界值以外的概率。 |
【本文地址】
| 今日新闻 |
| 推荐新闻 |
| 专题文章 |