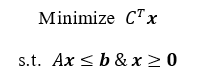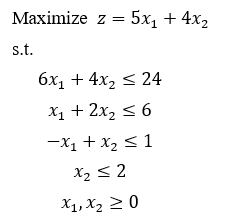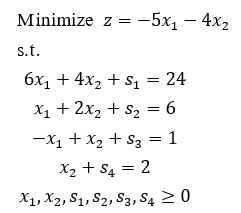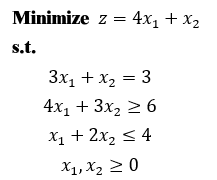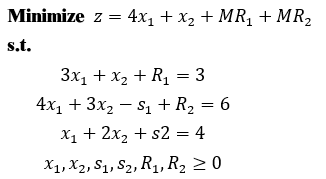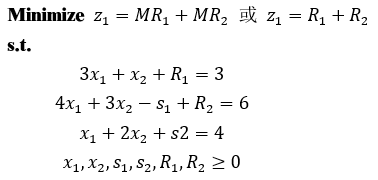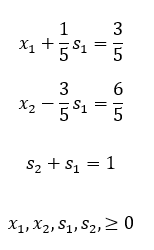线性规划单纯形（Simplex）算法总结与个人理解

关于线性单纯形算法的总结，具体包括单纯形算法，大M法，两阶段法以及单纯形法的一些特殊情况。

关于单纯形法的理解，主要参考了线性规划-单纯形算法详解。单纯形法的特殊情况参考了单纯形法的几种特殊情况。

这里不对单纯形算法的原理进行证明，但是给出自己对计算单纯形表的每一个步骤的理解。

一般线性规划可化为如下形式：

其中，b 可为正也可为负。当 b 中元素全为正时，显然 x = 0 是满足线性规划约束的一个基本可行解，可直接运用单纯形算法；当 b 中存在元素为负数时，需要运用大M法，或两阶段法先找到一个基本可行解。

以下述线性规划为例，说明单纯形算法：

步骤1：转化为最小化问题并添加松弛变量 ：

步骤2：构造初始单纯形表：

上表中，位于第一列的变量    称为基本变量；第一行中扣除基本变量后剩下的   称为非基本变量；z 为目标函数，solution 中 z 行的值为初始基本可行解 x=0 （非基本变量取0，基本变量取 solution 列的值）对应的 -z 的值。从    至   行代表对应的约束方程。

步骤3：用非基本变量替出基本变量

如上表，因为   且   ，所以增大变量    可以减小目标函数 z 。这里   的系数为 -5 ，增大   使 z 减小的最多，因此选择    作为替入变量。总结来说，便是选择 z 行中数值为负且最小的非基本变量为替入变量。

选定   列后，我们将 solution 列的值（不包括 z 行，下同）除以同行   列值，并选择比值为正且最小的那一行所对应的基本变量为替出变量，这里对应的是   行。之所以这么选择是基于以下理由：

1）选择    作为替入变量，   作为替出变量后，   的取值不再为零，   的取值为零，其他值保持不变。以    行为例，约束方程变为   ，即   。

2）替出变量   的选择应始终保证各变量仍满足大于等于 0 的条件。例如，    行系数为负，则    不符合条件；若取   行，则   ，代入    行后得到     小于0，也不符合条件。因此要选择 solution 列与    比值最小且为正所在行的基本变量为替出变量。

如果所有的比值结果都为非正数，则说明    取值无限制，线性规划问题无界。（这里可以这样考虑，当系数都为0或者负数时，任意大的   的取值均可满足所有约束方程，因为   右端为非负数，因此 z 可取负无穷，问题无界）

第一次替换后的结果如下：

这里    行是直接将原    行除以 6 所得，   均是对    行做初等行变换，使得其    列的值为0。对于 z 行，做行变换相当于用    行消去   ，代入后可以发现 solution 列中的 20 表示的是 - z 。因为 [] 是由线性方程组构成的矩阵，做初等行变换性质不变，个人认为这便是单纯形法的理论基础。

步骤4：重复步骤3，直到 z 行所有系数为非负。这里用    代替    可得最终结果：

因为原问题求的是最大值，所以这里的 21 就是原问题的最大值，对应最优解为  ， 

如果非基本变量 z 行的系数也为 0 ，例如这里如果    的系数不是 3/4 而是 0，那么则说明 z 取最小时，   的取值不限定。如果将矩阵再还原成线性方程组可以发现，5个未知数对应4个方程，所以原问题有无穷多最优解。也就是说，如果最终得到的矩阵中，存在非基本变量的 z 行系数为 0，那么线性规划问题有多重最优解。

当 b 中存在元素为负数时， 不是线性规划的一个基本可行解，因此不能直接运用上述方法。

b 中存在元素为负数，相当于约束中存在大于等于约束，现以下述例子说明大M法（事实上当存在大于等于或者等于约束时，运用大M法，对等式约束而言松弛变量相当于人工变量）。

添加人工变量 Ri ，原规划问题可写成：

大M法，顾名思义，M在这里为取值很大的正数，因此若原问题最小值存在，最优解必然使    和    为零，因此引入人工变量并无影响。

同样，列单纯形表（或称之为单纯形矩阵）：

利用    行和    行对 z 行做初等行变换，消去系数 M ，结果如下：

可以看到，引入人工变量  后使得基本变量的个数等于约束方程的个数，接下来按照普通单纯形法的步骤计算，注意 M 表示很大的正数。（结合后面的两阶段，也可认为这里用 M 来表示一个基本可行解）

第一次用    替出    得：

第二次用    替出    得：

第三次用    替出    得：

所以我们得到 - z = - 17/5，即 z 的最小值为 17/5，对应最优解为：，。

如果最后我们得到的结果中，仍存在人工变量 Ri 为基本变量且取值不为 0 ，则说明原问题无可行解。（可以认为必须要引入额外人工变量以后才能求解，但此时人工变量不为零，所求解的问题已经跟原问题不同了）

两阶段法相当于引入人工变量后，将原问题分成以下两个问题分阶段求解：

第一阶段：单独优化人工变量之和

最终结果为：

如果最后第一阶段的最优值不为零，则说明原问题无可行解（原问题改变了）。

根据本文之前的说明，单纯形矩阵的演变过程是初等行变换的过程，最后得到的方程组与原方程组等价。在第一阶段优化结束时，  和   需取 0 ，因此我们得到新的约束方程组：

第二阶段：在新的约束方程组下优化原问题。

初始单纯形表为：

相当于：

第一阶段相当于找到了一个基本可行解：

观察大M法与上述结果可以发现，两阶段法与大M法十分相似。

最后补充一个关于退化的说明。在求解过程中，可能会出现 z 行出现两个或两个以上的变量系数相等且都小于零，或者确定要替入的非基变量后，求比值确定替出的基本变量时可能出现两个或者两个以上的基本变量的比值相同或都为0，此时如果随便选择变量进行操作，可能会造成循环，无法求得最优解。出现的原因是模型中存在多余的约束，使多个基本可行解对应同一顶点。

当出现退化问题时，按照先决策变量，后松弛变量，再人工变量的顺序选择替入或替出变量。