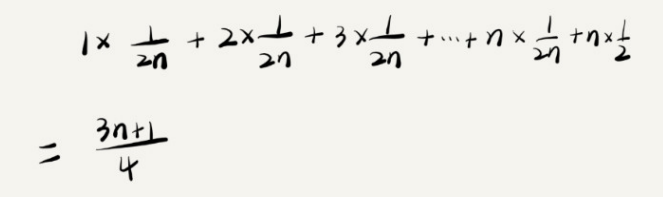算法：关于最好、最坏、平均、均摊时间复杂度

由于运行环境和输入规模的影响，代码的绝对执行时间是无法估计的，但是我们可以预估出代码的基本操作几次

关于代码的基本操作执行次数，我们用四个生活中的场景，来做一下比喻：

场景1：

给小灰一条长10寸的面包，小灰每3天吃掉1寸，那么吃掉整个面包需要几天？

答案自然是 3 X 10 = 30天。

如果面包的长度是 N 寸呢？

此时吃掉整个面包，需要 3 X n = 3n 天。

如果用一个函数来表达这个相对时间，可以记作 T（n） = 3n。

场景2：

场景3：

场景4：

上面所讲的是吃东西所花费的相对时间，这一思想同样适用于对程序基本操作执行次数的统计。刚才的四个场景，分别对应了程序中最常见的四种执行方式：

我们可以简单将时间复杂度理解为操作次数

有了基本操作执行次数的函数 T（n），是否就可以分析和比较一段代码的运行时间了呢？

所以，这时候有了–渐进时间复杂度**（asymptotic time complexity）的概念，官方的定义如下：

若存在函数 f（n），使得当n趋近于无穷大时，T（n）/ f（n）的极限值为不等于零的常数，则称 f（n）是T（n）的同数量级函数。

记作 T（n）= O（f（n）），称O（f（n）） 为算法的渐进时间复杂度，简称时间复杂度。

渐进时间复杂度用大写O来表示，所以也被称为大O表示法。 如何推导出时间复杂度呢？有如下几个原则：

让我们回头看看刚才的四个场景。

场景1：

场景2：

场景3：

场景4：

一般情况下只需要考虑最坏情况时间复杂度

如下代码表示在一个无序的数组（array）中，查找变量x 出现的位置。如果没有找到，就返回 -1。

这个时候，问题就来了。我们优化完之后，这段代码的时间复杂度还是 O(n) 吗？

所以，不同的情况下，这段代码的时间复杂度是不一样的。

为了表示代码在不同情况下的不同时间复杂度，我们需要引入三个概念：最好情况时间复杂度、最坏情况时间复杂度、平均情况时间复杂度。

顾名思义，最好情况时间复杂度就是，在最理想的情况下，执行这段代码的时间复杂度。比如上面，在最理想的情况下，要查找的变量 x 正好是数组的第一个元素，这个时候对应的时间复杂度就是最好情况时间复杂度。

同理，最坏情况时间复杂度就是，在最糟糕的情况下，执行这段代码的时间复杂度。就像刚举的那个例子，如果数组中没有要查找的变量 x，我们需要把整个数组都遍历一遍才行，所以这种最糟糕情况下对应的时间复杂度就是最坏情况时间复杂度。

最好情况时间复杂度和最坏情况时间复杂度对应的都是极端情况下的代码复杂度，发生的概率其实并不大。为了更好地表示平均情况下的复杂度，我们需要引入另一个概念：平均情况时间复杂度，简称为平均时间复杂度。

平均时间复杂度又该怎么分析呢？

这个结论虽然是正确的，但是计算过程稍微有点儿问题。究竟是什么问题呢？我们刚才说的这n+1中情况，出现的概率并不是一样的。

我们知道，要查找的变量 x，要么在数组里，要么就不在数组里。在数组中与不在数组中的概率都为 1/2。另外，要查找的数据出现在 0～n-1 这 n 个位置的概率也是一样的，为 1/n。所以，根据概率乘法法则，要查找的数据出现在 0～n-1 中任意位置的概率就是 1/(2n)。

因此，前面的推导过程中存在的最大问题就是，没有将各种情况发生的概率考虑进去。如果我们把每种情况发生的概率也考虑进去，那平均时间复杂度的计算过程就变成了这样：

实际上，在大多数情况下，我们并不需要区分最好、最坏、平均情况时间复杂度三种情况。很多时候，我们只用一个复杂度就可以满足需求了。只有同一块代码在不同的情况下，时间复杂度有量级的差距，我们才回使用这三种复杂度表示法来区分。

大部分情况下，我们并不需要区分最好、最坏、平均三种复杂度。平均复杂度只在某些特殊情况下才会用到，而均摊时间复杂度应用的场景比它更加特殊、更加有限。

举个例子。下面代码实现了往一个数组中插入数据的功能。当数组满了之后，也就是代码中的count == array.length时，我们用for循环遍历数组求和，并清空数组，将求和之后的sum值放到数组中的第一个位置，然后再将新的数据插入。但如果数组一开始就有空闲空间，则直接将数据插入数组。