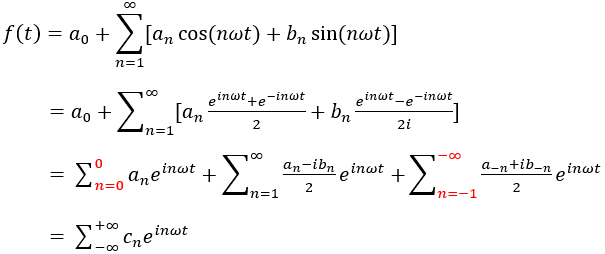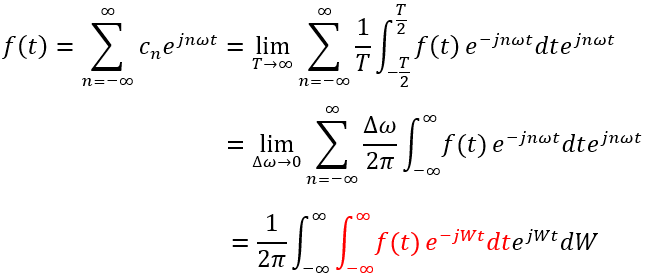图像处理:傅里叶变换

因为三角函数在-π到π内的积分为0，因此当m≠n时上面三个式子必定为0，因此可以得出以下结论， 频率不同的三角函数相乘在一个周期内(-π到π)的积分必定为0。

假设一函数f(t)由一个直流分量和若干正余弦函数组成

在上式两边同时乘以sin⁡(kωt)，并对它们在一个周期内进行积分，可得

化简得

因此，可得 bn，同理也可得 an

1.2 欧拉公式与傅里叶级数

根据 欧拉公式

当θ=nωt和θ=-nωt时，

将这两项代入傅里叶级数

当n=0时，代入上一小节得到的a0

当n=1,2,3,...时，代入an，bn

当n=-1,-2,-3,...时，代入an，bn

可以看出， 对于任意的n，所有Cn的表达式都是一样的，傅里叶级数最终可以写为：

得证。

2 傅里叶变换 2.1 连续傅里叶变换

傅立叶级数是针对周期函数的，而 傅里叶变换针对非周期函数， 一个非周期函数可以看做周期无限大的函数。当T趋于无穷大时，频率间隔 ω=2π/T趋于无穷小; Δω=(n+1)ω-nω=ω=2π/T，因此 Δω也趋于0， 1/T=Δω/2π;ΣΔω可以写成积分的形式 ∫dω。我们以 nω为变量，当 ω不等于0时， nω为离散值，，但当 ω趋于无穷小时， nω就变成连续的量 ，令 nω=W。

我们将这个式子中标红的部分称作 函数f(t)的傅里叶变换，记作F(w),即

而原始函数f(t)可以写为

我们称之为 傅里叶反变换。

二维连续函数f(x,y)的傅里叶正变换为

相应的傅里叶逆变换公式为

2.2 离散傅里叶变换

实际的信号往往是离散且有限的，在这种受限下要用到 离散傅里叶变换（Discrete Fourier Transform简称DFT)。首先，假设采集了N个信号点，其时间为 t 0 , t 1 , ... , t N-1 ，对应的信号值为 f(t 0 ), f(t 1 ), ... , f(t N-1 ) 。信号连续的时候是积分，现在数据离散了用累加，于是

我们发现，原信号有N个数据点，DFT变换后的信号却变成连续的了，我们将之称为 离散时间傅里叶变换（DISCRETE TIME FOURIER TRANSFORM，简称DTFT）。 DTFT有两个缺点，第一， ω∈(−∞,+∞)且连续， 需要进行无数次计算，计算机无法计算；第二，在进行计算的时候，我们 需要已知 t 0 , t 1 , ... , t N-1 ， 和 f(t 0 ), f(t 1 ), ... , f(t N-1 ) ，但是FFT函数只需要已知 f(t 0 ), f(t 1 ), ... , f(t N-1 ) 就可以进行。

我们可以采用相对时间n=0,1,...,N-1来代替真实采样时间 t 0 , t 1 , ... , t N-1 ， 可以得到

此时我们发现 F(ω)变成了以 2π为周期的函数，即

我们只需要计算 ω∈(0,2π)区间的 F(ω)，就可以得到 ω∈(−∞,+∞)区间的 F(ω)了。也就是说，通过使用相对采样时间 n=0,1,...N−1代替真实采样时间 t 0 , t 1 , ... , t N-1 ，我们将 F(ω)的范围从 (−∞,+∞)缩小到了 (0,2π)。再将 (0,2π)离散化为N个点，这样计算机就可以计算了，取 ω=2πk/N， k=0,1,...N−1，得 离散傅里叶变换DFT

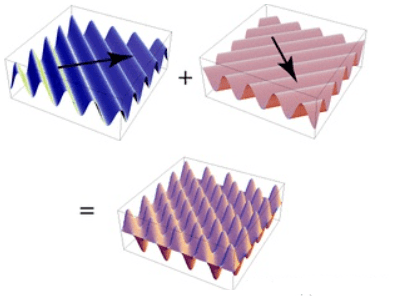
二维离散函数f(x,y)的傅里叶正变换的公式如下：

其中，u=0,1,2,...,M-1;v=0,1,2,...N-1。

相应的 傅里叶逆变换的公式如下：

其中，x=0,1,2,...,M-1;y=0,1,2,...N-1。

一维信号是一个序列，傅里叶变换将其分解成若干个一维的简单函数之和。二维信号可以说是一个图像， 二维傅里叶变换 将图像分解成若干个复平面波之和。通过上面的公式，我们可以计算出，每个平面波在图像重的成分是多少。从公式也可以看出，二维傅里叶变换就是将图像与每个不同频率的不同方向的复平面波做内积（先再求和），也就是一个求在基上投影的过程。 一维的正弦波可以通过三个参数确定，频率ω，幅度A和相位φ。因此在频域中，一维坐标表示频率，每个坐标对应的函数值F(ω)是一个复数，它的模|F(w)|就是幅度A，幅角∠F(w)就是相位。而二维正弦平面波需要四个参数，其中三个和一维一样（ 频率ω ，幅度A 和相位φ ），令一个是 方向n。如下图所示，两个平面波仅在方向参数上不同：

如何存储频率ω ，幅度A，相位φ和方向n这些参数呢？和一维一样， 幅度和 相位可以用一个 复数表示，复数的模是幅度，幅角是相位 。向量有方向和长度，可以用来表示方向和频率。一个向量n=（u,v)，向量的模√u2+v2代表这个平面波的频率，方向是平面波的方向，在该点的值F(u,v)表示幅度和相位。包含所有（u,v)点的矩阵是K空间，如下图所示

上图中，频谱图的中心为原点，即u=0，v=0，中间区域为低频，频率低周期大，条纹间隔宽，从中间向外，频率增大，平面波周期减小，条纹间隔小。图像区域灰度越高表示该频率平面波在图像中成分越多，由于低频表示图像灰度平稳区域，高频表示细节和边缘，所以图像主要是低频，频谱图中间灰度较高。在不同象限的点所代表的平面波方向不同。链接中有很多 图像的二维傅里叶变换频谱图，可以验证下自己弄懂了没。

3 应用

二维离散傅里叶变换(Two-Dimensional Discrete Fourier Transform)是一种数字变换方法，一般应用于 将图像从 空间域转至 频域，在 图像增强、 图像去噪、 图像边缘检测、 图像特征提取、 图像压缩等等应用中都起着极其重要的作用。

3.1 频域滤波

图像实质上是二维矩阵。将空间域（二维灰度数表）的图像转换到频域（频率数表）能够更直观地观察和处理图像，也更有利于进行频域滤波等操作。在博客 图像增强中介绍了不少常用的低通滤波器，也在博客 傅里叶变换中介绍过OpenCV中傅里叶变换的写法。接下来的这个示例和之前的写法有些不同。

示例 频域滤波