【机器学习笔记】：大话线性回归（二）拟合优度和假设检验

大家好，我是东哥。

前一篇文章给大家介绍了线性回归的模型假设，损失函数，参数估计，和简单的预测。具体内容请看下面链接：【机器学习笔记】：大话线性回归（一）

但其实还有很多问题需要我们解决：这个模型的效果如何？如何评判这个效果？开始线性模型的假设成立吗？如何验证这些假设？还会有其它问题会影响模型效果吗？带着这些问题我们开始本篇的内容。

线性回归拟合优度

线性回归假设检验

线性回归诊断

回归直线与各观测点的接近程度成为回归直线对数据的拟合优度。而评判直线拟合优度需要一些指标，其中一个就是判定系数。

我们知道，因变量y值有来自两个方面的影响：

（1）来自x值的影响，也就是我们预测的主要依据

（2）来自无法预测的干扰项ϵ的影响

如果一个回归直线预测非常准确，那么它就需要让来自x的影响尽可能的大，而让来自无法预测干扰项的影响尽可能的小，也就是说x影响占比越高，预测效果就越好。下面我们看一下如何定义这些影响，并形成指标。 S S T = ∑ ( y i − y ˉ ) 2 S S R = ∑ ( y i ^ − y ˉ ) 2 S S E = ∑ ( y i − y ^ ) 2 SST = \sum(y_i-\bar{y})^2 \\ SSR = \sum( \hat{y_i}-\bar{y})^2 \\ SSE = \sum( y_i- \hat{y})^2 \\ SST=∑(yi​−yˉ​)2SSR=∑(yi​^​−yˉ​)2SSE=∑(yi​−y^​)2

SST（总平方和）：变差总平方和

SSR（回归平方和）：由x与y之间的线性关系引起的y变化

SSE（残差平方和）：除x影响之外的其它因素引起的y变化

它们之间的关系是： S S T = S S R + S S E SST=SSR+SSE SST=SSR+SSE。根据我们前面的分析，SSR越高，则代表回归预测越准确，观测点越是靠近直线，也即 S S R / S S T SSR/SST SSR/SST越大，直线拟合越好。因此，判定系数的定义就自然的引出来了，我们一般称为R2。

R 2 = S S R S S T = ∑ ( y i ^ − y ˉ ) 2 ∑ ( y i − y ˉ ) 2 = 1 − ∑ ( y i − y ^ ) 2 ∑ ( y i − y ˉ ) 2 R^2 = \frac{SSR}{SST}=\frac{\sum( \hat{y_i}-\bar{y})^2}{\sum(y_i-\bar{y})^2}=1-\frac{\sum( y_i- \hat{y})^2 }{\sum(y_i-\bar{y})^2} R2=SSTSSR​=∑(yi​−yˉ​)2∑(yi​^​−yˉ​)2​=1−∑(yi​−yˉ​)2∑(yi​−y^​)2​

还是用上篇的数据为例，利用R2来测试一下拟合的效果是怎么样的。

可以看到最后的得分是0.97，说明拟合程度还是很不错的。

判定系数R2的意义是由x引起的影响占总影响的比例来判断拟合程度的。当然，我们也可以从误差的角度去评估，也就是用残差SSE进行判断。估计标准误差是均方残差的平方根，可以度量各实际观测点在直线周围散布的情况。

S e = ∑ ( y i − y ^ ) 2 n − 2 = S S E n − 2 = M S E S_e = \sqrt{\frac{\sum( y_i- \hat{y})^2 }{n-2}}=\sqrt{\frac{SSE}{n-2}}=\sqrt{MSE} Se​=n−2∑(yi​−y^​)2​ ​=n−2SSE​ ​=MSE ​

估计标准误差与判定系数相反，se反映了预测值与真实值之间误差的大小， S e S_e Se​越小说明拟合度越高，相反， S e S_e Se​越大说明拟合度越低。仍然用之前的数据集进行测试：

可以看到，平均的标准误差只有0.08，非常低，说明了拟合效果很不错，同时也证实了R2结果的正确性。

要想知道我们根据样本拟合的模型是否可以有效地预测或估计，我们需要对拟合的模型进行显著性检验。回归分析中的显著性检验主要包括两方面内容：线性关系检验；回归系数检验。

线性关系检验是指多个自变量x和因变量y之间的线性关系是否显著，它们之间是否可以用一个线性模型表示。检验统计量使用F分布，其定义如下： F = S S R / k S S R / ( n − k − 1 ) = M S R M S E ∼ F ( k , n − k − 1 ) F=\frac{SSR/k}{SSR/(n-k-1)}=\frac{MSR}{MSE}\sim F{(k,n-k-1)} F=SSR/(n−k−1)SSR/k​=MSEMSR​∼F(k,n−k−1)

SSR的自由度为：自变量的个数k

SSE的自由度为：n-k-1

利用F统计量，线性关系检验的一般步骤为：

（1）提出原假设和备择假设

H 0 : β 1 = β 2 = . . . = β k = 0 H 1 : β 1 , β 2 . . . β k 至 少 有 一 个 不 等 于 0 H_0:\beta_1=\beta_2=...=\beta_k=0 \\ H_1:\beta_1,\beta_2...\beta_k至少有一个不等于0 \\ H0​:β1​=β2​=...=βk​=0H1​:β1​,β2​...βk​至少有一个不等于0

（2）计算检验的统计量F

F = S S R / k S S R / ( n − k − 1 ) = M S R M S E ∼ F ( k , n − k − 1 ) F=\frac{SSR/k}{SSR/(n-k-1)}=\frac{MSR}{MSE}\sim F{(k,n-k-1)} F=SSR/(n−k−1)SSR/k​=MSEMSR​∼F(k,n−k−1)

（2）作出统计决策

与假设检验相同，如果给定显著性水平α，则根据两个自由度k和n-k-1进行F分布的查表。若图片，则拒绝原假设，说明发生了小概率事件，若图片，则不拒绝原假设。当然，我们也可以直接通过观察P值来决定是否拒绝原假设。

通过上面步骤的假设，我们也看到了：在多元线性回归中，只要有一个自变量系数不为零（即至少一个自变量系数与因变量有线性关系），我们就说这个线性关系是显著的。如果不显著，说明所有自变量系数均为零。

回归系数的显著性检验与线性检验不同，它要求对每一个自变量系数进行检验，然后通过检验结果可判断出自变量是否显著。因此，我们可以通过这种检验来判断一个特征（自变量）的重要性，并对特征进行筛选。检验统计量使用t分布，步骤如下：

（1）提出原假设和备择假设

对于任意参数 ( β i , i = 1 , 2 , . . . k ) (\beta_i,i=1,2,...k) (βi​,i=1,2,...k)，有： H 0 : β i = 0 H 1 : β i ≠ 0 H_0 :\beta_i=0 \\ H_1 :\beta_i\ne0 H0​:βi​=0H1​:βi​​=0 （2）计算检验统计量t t i = β ^ i s β ^ i ∼ t ( n − k − 1 ) s β ^ i = s e ∑ x i 2 − 1 n ( ∑ x i ) 2 t_i=\frac{\hat{\beta}_i}{s_{\hat{\beta}_i}}\sim t(n-k-1) \\ s_{\hat{\beta}_i}=\frac{s_e}{\sqrt{\sum{x_i}^2-\frac{1}{n}(\sum{x_i})^2}} ti​=sβ^​i​​β^​i​​∼t(n−k−1)sβ^​i​​=∑xi​2−n1​(∑xi​)2 ​se​​

（3）作出统计决策

如前面一样，我们需要根据自由度 n − k − 1 n-k-1 n−k−1查t分布表，并通过α或者p值判断显著性。

下面通过一段代码来说明上面两种显著性检验，为了方便我们直接通过statsmodels模型引入ols模型进行回归拟合，然后查看总结表，其中包括F和t统计量结果。

通过上面结果我们清楚看到：

F统计量的p值非常小，拒绝原假设，说明线性关系显著

两个回归系数的t统计量p值均为0，拒绝原假设，说明回归系数也都显著

线性回归的诊断包括很多内容，比较重要的几个有：

（1）残差分析

（2）线性相关性检验

（3）多重共线性分析

（4）强影响点分析

下面我们开始分别介绍这几个需要诊断的内容。

还记得我们的模型是怎么来的吗？没错，线性回归模型是基于一些假设条件的：除了自变量和因变量有线性相关关系外，其它假设基本都是关于残差的，主要就是残差 ϵ ϵ ϵ独立同分布，服从 N ∼ ( 0 , σ 2 ) N\sim(0,\sigma^2) N∼(0,σ2)。

总结一下关于残差有三点假设：

下面我们将对这些假设逐一诊断，只有假设被验证，模型才是成立的。

干扰项（即残差），服从正态分布的本质是要求因变量服从变量分布。 因此，验证残差是否服从正态分布就等于验证因变量的正态分布特性。关于正态分布的检验通常有以下几种方法。

（1）直方图法：

直方图法就是根据数据分布的直方图与标准正态分布对比进行检验，主要是通过目测。比如本例中我们的直方图可以这样显示出来：

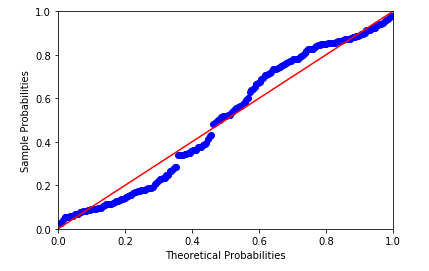
通过目测，我们发现残差的数据分布并不是很好的服从正态分布，因此这里是不满足假设条件的。

（2）PP图和QQ图：

PP图是对比正态分布的累积概率值和实际分布的累积概率值。statsmodels中直接提供了该检测方法：

QQ图是通过把测试样本数据的分位数与已知分布相比较，从而来检验数据的分布情况。对应于正态分布的QQ图，就是由标准正态分布的分位数为横坐标，样本值为纵坐标的散点图。 同样的，我们通过一段代码来观察一下：

pp图和qq图判断标准是：如果观察点都比较均匀的分布在直线附近，就可以说明变量近似的服从正态分布，否则不服从正态分布。

从pp图和qq图可以看出，样本点并不是十分均匀地落在直线上，有的地方有一些较大的偏差，因此判断不是正态分布。

（3）Shapiro检验：

这种检验方法均属于非参数方法，先假设变量是服从正态分布的，然后对假设进行检验。一般地数据量低于5000则可以使用Shapiro检验，大于5000的数据量可以使用K-S检验，这种方法在scipy库中可以直接调用：

上面结果两个参数：第一个是Shaprio检验统计量值，第二个是相对应的p值。可以看到，p值非常小，远远小于0.05，因此拒绝原假设，说明残差不服从正态分布。

同样的方法还有KS检验，也可以直接通过scipy调用进行计算。

残差的独立性可以通过Durbin-Watson统计量（DW）来检验。

原假设： p = 0 p=0 p=0（即前后扰动项不存在相关性）

背责假设： p ≠ 0 p\ne0 p​=0（即近邻的前后扰动项存在相关性）

DW统计量公式如下：

D W = ∑ t = 2 T ( u t ^ − u t − 1 ^ ) 2 ∑ t = 1 T u t ^ 2 = 2 ( 1 − p ^ ) DW=\frac{\sum_{t=2}^{T}{(\hat{u_t}-\hat{u_{t-1}})^2}}{\sum_{t=1}^{T}{\hat{u_t}^2}}=2(1-\hat{p}) DW=∑t=1T​ut​^​2∑t=2T​(ut​^​−ut−1​^​)2​=2(1−p^​)

判断标准是：

p=0，DW=2：扰动项完全不相关

p=1，DW=0：扰动项完全正相关

p=-1，DW=4：扰动项完全负相关

在我们前面使用的statsmodels结果表中就包含了DW统计量：

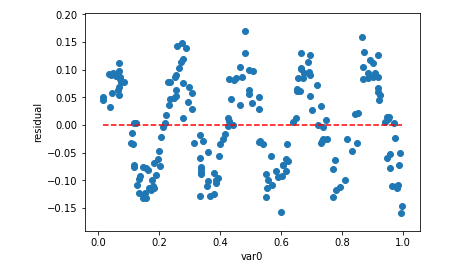
DW值为2.192，说明残差之间是不相关的，也即满足独立性假设。

如果残差随着自变量增发生随机变化，上下界基本对称，无明显自相关，方差为齐性，我们就说这是正常的残差。判断方差齐性检验的方法一般有两个：图形法，BP检验。

（1）图形法

图形法就是画出自变量与残差的散点图，自变量为横坐标，残差为纵坐标。下面是残差图形的代码：

图形法可以看出：残差的方差（即观察点相对红色虚线的上下浮动大小）不随着自变量变化有很大的浮动，说明了残差的方差是齐性的。

如果残差方差不是齐性的，有很多修正的方法，比如加权最小二乘法，稳健回归等，而最简单的方法就是对变量取自然对数。而取对数从业务上来说也是有意义的，解释变量和被解释变量的表达形式不同，对回归系数的解释也不同。下面是不同转换情况下的解释：

对数转换后的效果可以通过R2或者修改R2的结果比对得出，如果方差通过取对数变换变成齐性，那么它的R2应该比变换之前数值高，即会取得更好的效果。

（2）BP检验法

这种方法也是一种假设检验的方法，其原假设为：残差的方差为一个常数，然后通过计算LM统计量，判断假设是否成立。在statsmodels中也同样有相应的方法可以实现BP检查方法。

上述参数：

第一个为：LM统计量值

第二个为：响应的p值，0.68远大于显著性水平0.05，因此接受原假设，即残差方差是一个常数

第三个为：F统计量值，用来检验残差平方项与自变量之间是否独立，如果独立则表明残差方差齐性

第四个为：F统计量对应的p值，也是远大于0.05的，因此进一步验证了残差方差的齐性。

参考：

统计学，贾俊平

计量经济学导论，伍德里奇

从零开始学Python数据分析与挖掘，刘顺祥

Python数据科学技术详解与商业实践，常国珍

原创不易，欢迎点赞。

欢迎关注东哥的原创公众号：Python数据科学