| 大学物理电磁学 | 您所在的位置:网站首页 › 电磁学三大基本定律公式 › 大学物理电磁学 |
大学物理电磁学
|
毕奥·萨伐尔定律
公式汇总:
一般公式: d B = μ 0 4 π I d l ⃗ × r ⃗ r 3 = μ 0 4 π I d l s i n α r 2 dB=\frac{\mu_0}{4\pi}\frac{I\vec{dl}\times\vec{r}}{r^3}=\frac{\mu_0}{4\pi}\frac{Idlsin\alpha}{r^2} dB=4πμ0r3Idl ×r =4πμ0r2Idlsinα B ⃗ = ∫ d B ⃗ = ∫ μ 0 4 π I d l ⃗ × r ⃗ r 3 \vec{B}=\int d\vec{B}=\int \frac{\mu_0}{4\pi}\frac{I\vec{dl}\times\vec{r}}{r^3} B =∫dB =∫4πμ0r3Idl ×r 载流直导线的磁场: B = μ 0 I 4 π a ( c o s α 1 − c o s α 2 ) B=\frac{\mu_0I}{4\pi a}(cos\alpha_1-cos\alpha_2) B=4πaμ0I(cosα1−cosα2) 无限长载流直导线: B = μ 0 I 2 π a B=\frac{\mu_0I}{2\pi a} B=2πaμ0I 载流圆线圈轴上的磁场: B = μ 0 I R 2 2 ( R 2 + x 2 ) 3 2 B=\frac{\mu_0IR^2}{2(R^2+x^2)^{\frac{3}{2}}} B=2(R2+x2)23μ0IR2 圆心处: x = 0 , B 0 = μ 0 I 2 R x=0,B_0=\frac{\mu_0I}{2R} x=0,B0=2Rμ0I 通电螺线管: B = μ 0 n I 2 ( x 2 √ x 2 2 + R 2 − x 1 √ x 1 2 + R 2 ) B=\frac{\mu_0nI}{2}(\frac{x_2}{\surd{x_2^2+R^2}}-\frac{x_1}{\surd{x_1^2+R^2}}) B=2μ0nI(√x22+R2x2−√x12+R2x1) 对于无限长的螺线管: B = μ 0 n I B=\mu_0nI B=μ0nI 1. 磁现象 一切磁现象都源于电荷的运动。一切磁力本质上都是电荷之间的作用力。一切磁现象都源于电荷运动,磁相互作用的本质就是运动电荷(电流)之间的运动。 激发 作用于 运动电荷 载流导线 磁体 磁场 运动电荷 载流导线 磁体稳恒磁场:由稳恒电流激发的磁场。 2. 毕奥·萨伐尔定律 2.1 电流元定义: I d l ⃗ I\vec{dl} Idl 为电流元。大小为 I d l Idl Idl, d l ⃗ \vec{dl} dl 的方向由线元所在处电流的流向来确定。 目的:用积分法来求出任意形状的磁场分布。 2.2 电流元的磁场大小: d B = μ 0 4 π I d l ⃗ × r ⃗ r 3 = μ 0 4 π I d l s i n α r 2 dB=\frac{\mu_0}{4\pi}\frac{I\vec{dl}\times\vec{r}}{r^3}=\frac{\mu_0}{4\pi}\frac{Idlsin\alpha}{r^2} dB=4πμ0r3Idl ×r =4πμ0r2Idlsinα 真空磁导率: μ 0 = 4 π × 1 0 − 7 N ⋅ A − 2 \mu_0=4\pi\times10^{-7}N\cdot A^{-2} μ0=4π×10−7N⋅A−2 运用积分: B ⃗ = ∫ d B ⃗ = ∫ μ 0 4 π I d l ⃗ × r ⃗ r 3 \vec{B}=\int d\vec{B}=\int \frac{\mu_0}{4\pi}\frac{I\vec{dl}\times\vec{r}}{r^3} B =∫dB =∫4πμ0r3Idl ×r 说明:毕奥·萨伐尔定律只适用于恒定电流。解题步骤: 建立坐标系。分割电流元。确定电流元的磁场。坐标分解求 d B dB dB的分量 d B x dB_x dBx, d B y dB_y dBy, d B z dB_z dBz,然后统一积分变量求出 d B x dB_x dBx, d B y dB_y dBy, d B z dB_z dBz。由 B ⃗ = d B x i ⃗ + d B y j ⃗ + d B z k ⃗ \vec{B}=dB_x\vec{i}+dB_y\vec{j}+dB_z\vec{k} B =dBxi +dByj +dBzk ,求总场。 毕奥·萨伐尔定律运用实例 载流直导线的磁场 B = μ 0 I 4 π a ( c o s α 1 − c o s α 2 ) B=\frac{\mu_0I}{4\pi a}(cos\alpha_1-cos\alpha_2) B=4πaμ0I(cosα1−cosα2) 其中,a是点到导线的垂直距离。 α 1 \alpha_1 α1是电流入端点与该点与待求点连线之间的夹角。
B = μ 0 I R 2 2 ( R 2 + x 2 ) 3 2 B=\frac{\mu_0IR^2}{2(R^2+x^2)^{\frac{3}{2}}} B=2(R2+x2)23μ0IR2 这里的x是待求点到圆线圈圆心处的距离。 圆心处: x = 0 , B 0 = μ 0 I 2 R x=0,B_0=\frac{\mu_0I}{2R} x=0,B0=2Rμ0I 如果是圆弧形的电流: B 0 = μ 0 I 2 R θ 2 π B_0=\frac{\mu_0I}{2R}\frac{\theta}{2\pi} B0=2Rμ0I2πθ 载流密绕直螺线管轴上的磁场
 −
e
-e
−e的原因是,I 的方向与负电荷运动方向相反。带电圆环已知每秒绕N转,与之前类似,T=1/N。
3. 磁距
−
e
-e
−e的原因是,I 的方向与负电荷运动方向相反。带电圆环已知每秒绕N转,与之前类似,T=1/N。
3. 磁距
平面载流线圈的磁距: p ⃗ m = I S ⃗ \vec{p}_m=I\vec{S} p m=IS S ⃗ \vec{S} S 的方向就是法向量的方向。 载流线圈轴线上距圆心很远的场可表示为: B = μ 0 I R 2 2 x 3 = μ 0 I π R 2 2 π x 3 = μ 0 I S ⃗ 2 π x 3 = μ 0 p m 2 π x 3 B=\frac{\mu_0IR^2}{2x^3}=\frac{\mu_0I\pi R^2}{2\pi x^3}=\frac{\mu_0 I\vec{S}}{2\pi x^3}=\frac{\mu_0 p_m}{2\pi x^3} B=2x3μ0IR2=2πx3μ0IπR2=2πx3μ0IS =2πx3μ0pm 考虑方向: B ⃗ = μ 0 p ⃗ m 2 π x 3 \vec{B}=\frac{\mu_0\vec{p}_m}{2\pi x^3} B =2πx3μ0p m 当圆电流的半径很小或者讨论远离圆电流处的磁场分布时,把圆电流称作磁偶极子,产生的磁场称为磁偶极磁场。 |
【本文地址】
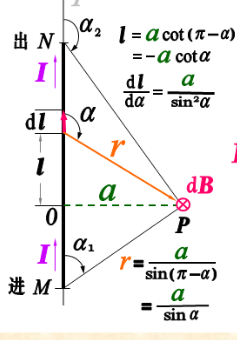
 我当时上课的时候感觉很疑惑,这里的n匝线圈明明是串联的,为什么
d
I
=
n
d
x
I
dI=ndxI
dI=ndxI呢? 其实不需要管这里的电流是串联还是并联,因为我们在这里是要考虑电流产生的磁感性强度,所以n匝电流产生的是n倍,或者我们可以从上面讲的载流圆线圈的圆弧形式理解,
B
0
=
μ
0
I
2
R
θ
2
π
B_0=\frac{\mu_0I}{2R}\frac{\theta}{2\pi}
B0=2Rμ0I2πθ,绕两圈就是
θ
=
4
π
\theta = 4\pi
θ=4π,以此类推。 回到上面的微元形式进行积分。 这里把P点看作是坐标原点,对dx进行积分得:
B
=
μ
0
n
I
2
(
x
2
√
x
2
2
+
R
2
−
x
1
√
x
1
2
+
R
2
)
B=\frac{\mu_0nI}{2}(\frac{x_2}{\surd{x_2^2+R^2}}-\frac{x_1}{\surd{x_1^2+R^2}})
B=2μ0nI(√x22+R2x2−√x12+R2x1) 对于无限长的螺线管,
B
=
μ
0
n
I
B=\mu_0nI
B=μ0nI
我当时上课的时候感觉很疑惑,这里的n匝线圈明明是串联的,为什么
d
I
=
n
d
x
I
dI=ndxI
dI=ndxI呢? 其实不需要管这里的电流是串联还是并联,因为我们在这里是要考虑电流产生的磁感性强度,所以n匝电流产生的是n倍,或者我们可以从上面讲的载流圆线圈的圆弧形式理解,
B
0
=
μ
0
I
2
R
θ
2
π
B_0=\frac{\mu_0I}{2R}\frac{\theta}{2\pi}
B0=2Rμ0I2πθ,绕两圈就是
θ
=
4
π
\theta = 4\pi
θ=4π,以此类推。 回到上面的微元形式进行积分。 这里把P点看作是坐标原点,对dx进行积分得:
B
=
μ
0
n
I
2
(
x
2
√
x
2
2
+
R
2
−
x
1
√
x
1
2
+
R
2
)
B=\frac{\mu_0nI}{2}(\frac{x_2}{\surd{x_2^2+R^2}}-\frac{x_1}{\surd{x_1^2+R^2}})
B=2μ0nI(√x22+R2x2−√x12+R2x1) 对于无限长的螺线管,
B
=
μ
0
n
I
B=\mu_0nI
B=μ0nI