| 开关电源补偿环路设计基础 | 您所在的位置:网站首页 › 电源补偿器 › 开关电源补偿环路设计基础 |
开关电源补偿环路设计基础
|
开关电源控制环路基础
补偿网路基本知识基本常识常用系统介绍
K因子推导补偿网络I型补偿II型补偿III型补偿
PI补偿和PID补偿PI补偿(IIa型补偿)IIb型补偿PID 补偿
补偿网路基本知识
基本常识
1.穿越频率(cross frequency):增益曲线穿越0dB的频率点; 2.相角裕度(Phase Margin):相位曲线在fc处的相位与-180度的差; 3.增益裕度(Gain Margin):增益曲线在相位曲线达到-180度的频率处对应的增益(当相位曲线趋近于-180度时,增益为无穷大) 4.带宽:增益曲线下降3dB时的频率(一般带宽只考虑fH,fL-> 0Hz)。系统的单位阶跃响应的速度和带宽成正比。带宽越大,表明系统对控制信号的跟踪能力越强,但对高频的抑制效果减弱(增益曲线上高频噪声仍有较大的值) 5.0dB穿越极点,这个是指考虑初始极点的曲线穿越0dB时的频率。 6.中频增益:刚开始系统以-20dB/dec衰减,遇到一个零点时,保持的增益称为中频增益。例如G= (1+s/Wz)/(s/Wp)的中频增益G0=Wp/Wz; 7.最小相位系统:系统的闭环传递函数极点和零点的实部都小于或等于零(左半平面),则称它是最小相位系统,如果开环传递函数中有正实部的零点或极点,或有延迟环节,则称系统是非最小相位系统 8.零点、极点等;奈奎斯特图、波特图等基本知识 9.电路稳定的原则是:开环总增益为1的穿越频率处的开环总相移小于360,并留有一定的裕量;穿越0dB时的斜率为-20dB/dec 常用系统介绍1.单个极点,引入一个-1(-20dB/dec)的斜率和一个90度滞后
H
(
s
)
=
1
1
+
s
w
p
H(s)=\cfrac{1}{1+\cfrac{s}{w_p}}
H(s)=1+wps1 2.单个零点,引入一个+1斜率和一个90度超前
H
(
s
)
=
1
+
s
w
z
1
H(s)=\cfrac{1+\cfrac{s}{w_z}}{1}
H(s)=11+wzs 3.反向零点,引入一个-1斜率和一个90度超前
H
(
s
)
=
1
+
w
z
s
1
H(s)=\cfrac{1+\cfrac{w_z}{s}}{1}
H(s)=11+swz 4.右半平面零点,引入一个+1斜率和一个90度滞后
H
(
s
)
=
1
−
s
w
z
1
H(s)=\cfrac{1-\cfrac{s}{w_z}}{1}
H(s)=11−wzs 5.共轭复极点(不考虑C的esr时的LCR输出滤波传递函数)
H
(
s
)
=
1
s
2
ω
0
2
+
2
ζ
s
ω
0
+
1
=
1
s
2
ω
0
2
+
s
ω
0
Q
+
1
H(s)=\cfrac{1}{\cfrac{s^{2}}{\omega_{0}^{2}}+2 \zeta \cfrac{s}{\omega_{0}}+1}=\cfrac{1}{\cfrac{s^{2}}{\omega_{0}^{2}}+\cfrac{s}{\omega_{0} Q}+1}
H(s)=ω02s2+2ζω0s+11=ω02s2+ω0Qs+11 其中,2
ζ
\zeta
ζ称为临界阻尼
w
0
=
1
L
C
Q
=
R
C
L
=
1
2
ζ
w_0=\sqrt{\cfrac{1}{LC}}\\ Q=R\sqrt{\cfrac{C}{L}}=\cfrac{1}{2\zeta}
w0=LC1
Q=RLC
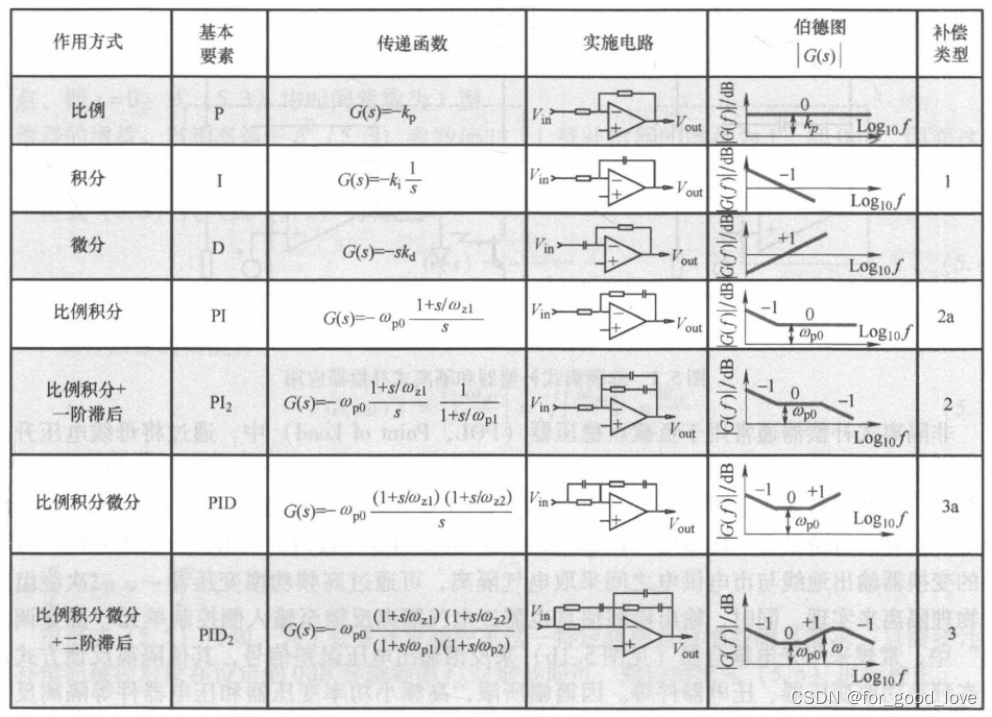
=2ζ1 6.一般表达式(不含有初始极点) G ( s ) = N ( s ) D ( s ) = G o ( 1 + s z 1 ) ( 1 + s z 2 ) ⋯ ( 1 + s z m ) ( 1 + s p 1 ) ( 1 + s p 2 ) ⋯ ( 1 + s p n ) = G o ( 1 + s 1 / z 1 ) ( 1 + s 1 / z 2 ) ⋯ ( 1 + s 1 / z m ) ( 1 + s 1 / p 1 ) ( 1 + s 1 / p 2 ) ⋯ ( 1 + s 1 / p n ) \begin{align} G(s)=\cfrac{N(s)}{D(s)}=&G_o\cfrac{(1+sz_1)(1+sz_2)\cdots(1+sz_m)}{(1+sp_1)(1+sp_2)\cdots(1+sp_n)}\\=&G_o\cfrac{\left(1+\cfrac{s}{1/z_1}\right)\left(1+\cfrac{s}{1/z_2}\right)\cdots\left(1+\cfrac{s}{1/z_m}\right)}{\left(1+\cfrac{s}{1/p_1}\right)\left(1+\cfrac{s}{1/p_2}\right)\cdots\left(1+\cfrac{s}{1/p_n}\right)} \end{align} G(s)=D(s)N(s)==Go(1+sp1)(1+sp2)⋯(1+spn)(1+sz1)(1+sz2)⋯(1+szm)Go(1+1/p1s)(1+1/p2s)⋯(1+1/pns)(1+1/z1s)(1+1/z2s)⋯(1+1/zms) 含有初始极点,标准写法将含有初始极点的改写成含有反相零点 G ( s ) = N ( s ) D ( s ) = G o ( 1 + s z 1 ) ( 1 + s z 2 ) ⋯ ( 1 + s z m ) s p 0 ( 1 + s p 1 ) ( 1 + s p 2 ) ⋯ ( 1 + s p n ) = G o G 1 ( 1 + 1 / z 1 s ) ( 1 + s 1 / z 2 ) ⋯ ( 1 + s 1 / z m ) ( 1 + s 1 / p 1 ) ( 1 + s 1 / p 2 ) ⋯ ( 1 + s 1 / p n ) \begin{align} G(s)=\cfrac{N(s)}{D(s)}=&G_o\cfrac{(1+sz_1)(1+sz_2)\cdots(1+sz_m)}{sp_0(1+sp_1)(1+sp_2)\cdots(1+sp_n)}\\=&G_o G_1\cfrac{\left(1+\cfrac{1/z_1}{s}\right)\left(1+\cfrac{s}{1/z_2}\right)\cdots\left(1+\cfrac{s}{1/z_m}\right)}{\left(1+\cfrac{s}{1/p_1}\right)\left(1+\cfrac{s}{1/p_2}\right)\cdots\left(1+\cfrac{s}{1/p_n}\right)} \end{align} G(s)=D(s)N(s)==Gosp0(1+sp1)(1+sp2)⋯(1+spn)(1+sz1)(1+sz2)⋯(1+szm)GoG1(1+1/p1s)(1+1/p2s)⋯(1+1/pns)(1+s1/z1)(1+1/z2s)⋯(1+1/zms) 或者将基本环节分为比例、微分、积分、滞后等,如图所示
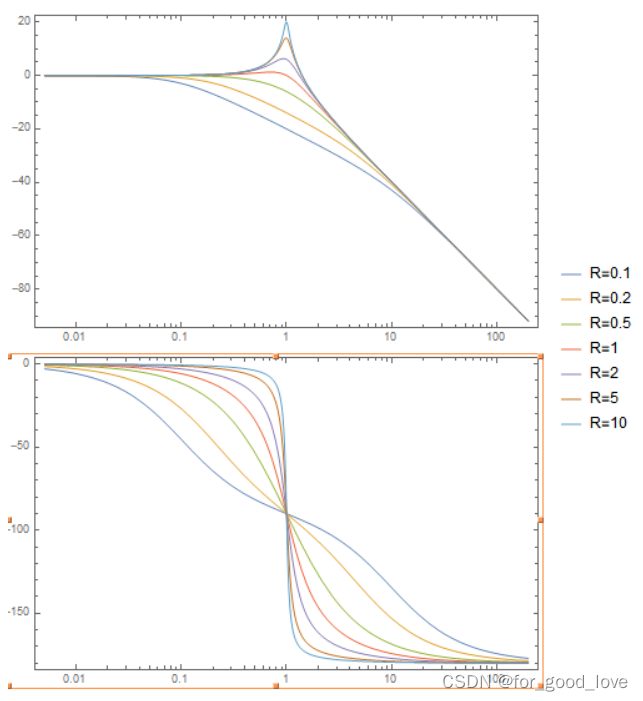
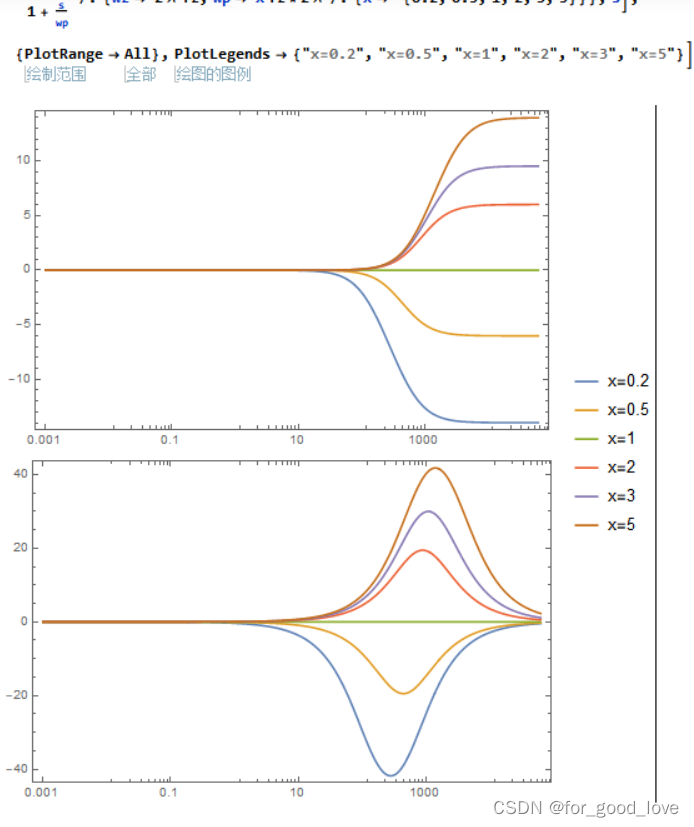
以一对零极点为例 G ( s ) = 1 + s / w z 1 + s / w p G(s)=\cfrac{1+s/w_z}{1+s/w_p} G(s)=1+s/wp1+s/wz 上述相角(或者认为是一对零极点所能做到提升的相位角大小)为 B o o s t = A r g ( G ( j w ) ) = a r c t a n ( w w z ) − a r c t a n ( w w p ) Boost=Arg(G(jw))=arctan(\cfrac{w}{w_z})-arctan(\cfrac{w}{w_p}) Boost=Arg(G(jw))=arctan(wzw)−arctan(wpw) 对上式进行求导有 d d f ( a r c t a n ( f f z − a r c t a n ( f f p ) ) ) = 1 f z ( 1 + f 2 f z 2 ) − 1 f z ( 1 + f 2 f p 2 ) = 0 \cfrac{d}{df}\left(arctan(\cfrac{f}{f_z}-arctan(\cfrac{f}{f_p}))\right)=\cfrac{1}{f_z(1+\cfrac{f^2}{f_z^2})}-\cfrac{1}{f_z(1+\cfrac{f^2}{f_p^2})}= 0 dfd(arctan(fzf−arctan(fpf)))=fz(1+fz2f2)1−fz(1+fp2f2)1=0 导数为0解得下式,这表明,当fp,fz已知时,选取在其几何均值具有最大的相位提升。 f c = f z f p f_c=\sqrt{f_zf_p} fc=fzfp 反过来可以探讨当fc处于fp,fz的几何均值时,fp与fz的关系,探讨此时最大的相角提升,当如图显示了当fp=xfz时的相位提升。
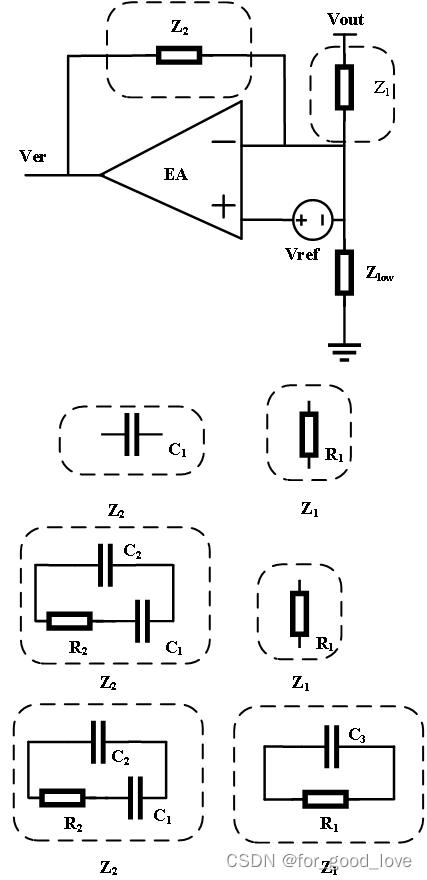
理论上,一对零极点可以提供的相角为(-90,90) 引入k因子,k=fp/fz,那么提升的角度为 B o o s t = a r c t a n ( k ) − a r t a n ( 1 k ) = 2 a r c t a n ( k ) − π 2 Boost=arctan(k)-artan(\cfrac{1}{k})=2arctan(k)-\cfrac{\pi}{2} Boost=arctan(k)−artan(k1)=2arctan(k)−2π 解得 k = t a n ( π 4 + b o o s t 2 ) f p = k f c , f z = f c / k k=tan(\cfrac{\pi}{4}+\cfrac{boost}{2})\\ fp=kfc,fz=fc/k k=tan(4π+2boost)fp=kfc,fz=fc/k 显然,上述方程是只需要知道两个未知数,通常是提升的角度和穿越频率,那么零极点即可求。当然当已知三个未知数时,上述k因子法不再试用,只需要解相位角方程即可求。 补偿网络补偿网络的传递函数是通过,mathematical 计算出零极点 G ( s ) = V e r r ( s ) V o u t ( s ) = − Z 2 Z 1 G(s)=\cfrac{V_{err}(s)}{V_{out}(s)}=-\cfrac{Z_2}{Z_1} G(s)=Vout(s)Verr(s)=−Z1Z2 基本补偿结构如图
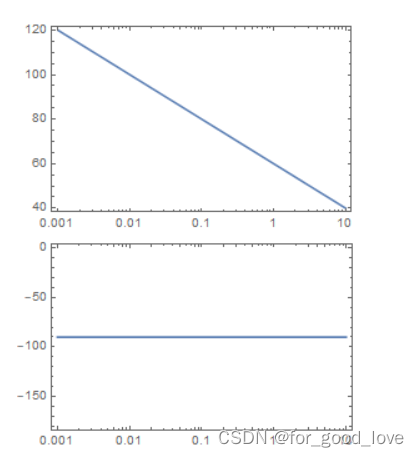
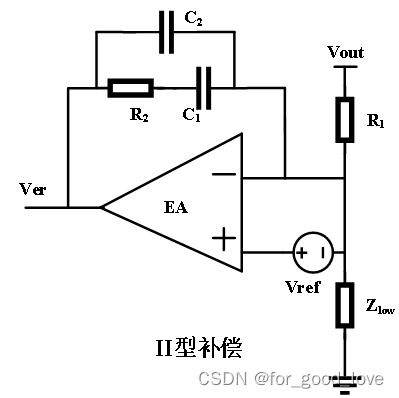
I型补偿只有一个初始极点(原点极点),提供-1斜率和90度滞后 II型补偿
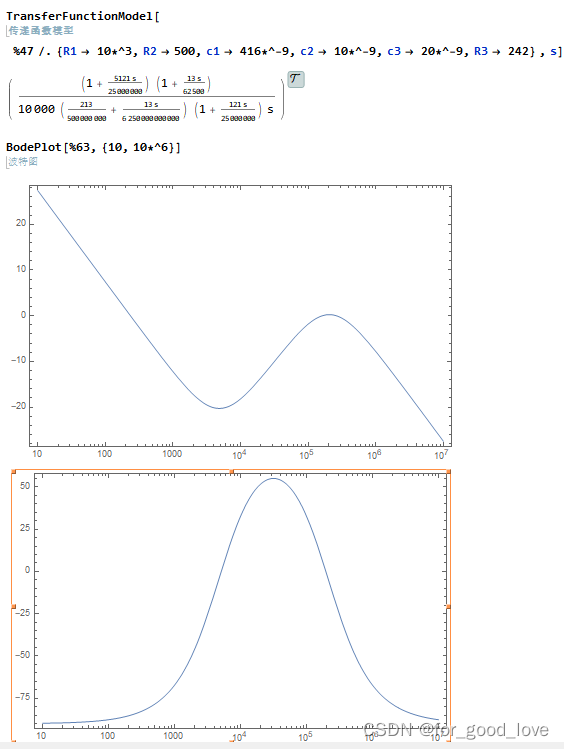
G s = − Z f Z i = 1 s C 2 / / ( R 2 + 1 s C 2 ) R 1 = − 1 + s R 2 C 1 s R 1 ( C 1 + C 2 ) ( 1 + s R 2 [ C 1 C 2 C 1 + C 2 ] ) = − R 2 R 1 C 1 C 1 + C 2 1 + 1 / s R 2 C 1 [ 1 + s 1 / C 1 + C 2 R 2 C 1 C 2 ] = − G 0 1 + w z / s 1 + s / w p \begin{align}G_{s}&=-\cfrac{Z_f}{Z_i}=\cfrac{\cfrac{1}{sC_2}//(R_2+\cfrac{1}{sC_2})}{R_1}\\&=-\frac{1+s R_{2} C_{1}}{s R_{1}\left(C_{1}+C_{2}\right)\left(1+s R_{2}\left[\cfrac{C_{1} C_{2}}{C_{1}+C_{2}}\right]\right)}\\&=-\frac{R_{2}}{R_{1}} \frac{C_{1}}{C_{1}+C_{2}}\cfrac{1+1 / s R_{2} C_{1}}{\left[1+\cfrac{s}{1/\frac{C_1+C_2}{R_2C_1C_2}}\right]}\\&=-G_{0} \frac{1+w_{z} / s}{1+s / w_{p}}\end{align} Gs=−ZiZf=R1sC21//(R2+sC21)=−sR1(C1+C2)(1+sR2[C1+C2C1C2])1+sR2C1=−R1R2C1+C2C1[1+1/R2C1C2C1+C2s]1+1/sR2C1=−G01+s/wp1+wz/s { G 0 = R 2 R 1 C 1 C 1 + C 2 ≈ R 2 R 1 C 1 > > C 2 w z = 1 R 2 C 1 w p = 1 R 2 C 1 C 2 C 1 + C 2 ≈ 1 R 2 C 2 \left\{\begin{align} &G_{0}=\cfrac{R_{2}}{R_{1}} \cfrac{C_{1}}{C_{1}+C_{2}}\approx \cfrac{R_2}{R_1}\qquad C_1>> C_2\\ &w_{z}=\cfrac{1}{R_{2} C_{1}} \\ &w_{p}=\cfrac{1}{R_{2} \cfrac{C_{1} C_{2}}{C_{1}+C_{2}}}\approx \cfrac{1}{R_2C_2} \end{align} \right. ⎩ ⎨ ⎧G0=R1R2C1+C2C1≈R1R2C1>>C2wz=R2C11wp=R2C1+C2C1C21≈R2C21
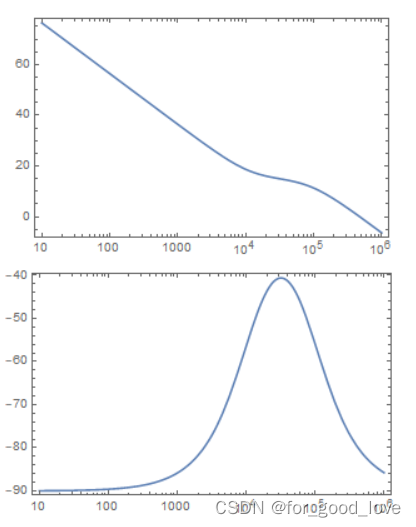
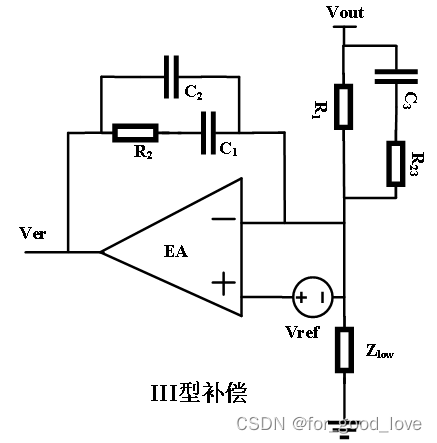
上述表明,在C1>>C2时,中频增益是R2/R1,极点是由C1和C2的串(串联容值变小,RC频率增大)与R2形成的极点,而零点是由R2和C1形成。这很好理解,由于C1>>C2,在频率较低时(1/wC2较大),C1发挥零点作用。此时的中频增益是近视为R2/R1;随着频率继续增大,R2串C1支路逐渐不变,而C2支路开始起作用,此时的极点(增益变小)是C1,C2和R2共同提供极点。同时可以知道,上式提供了一对零极点,相位(-90,90)变化,不过通常都是fp>>fz,即提供相位提升。 III型补偿
G
s
=
(
1
s
C
1
+
R
2
)
1
s
C
2
/
(
1
s
C
1
+
R
2
)
+
1
s
C
2
(
1
s
C
3
+
R
3
)
R
1
/
(
1
s
C
3
+
R
3
)
+
R
1
=
R
2
C
1
R
1
(
C
1
+
C
2
)
1
s
R
2
C
1
+
1
1
+
s
R
2
C
1
C
2
C
1
+
C
2
s
C
3
(
R
1
+
R
3
)
+
1
s
R
3
C
3
+
1
=
G
0
(
1
+
ω
z
1
s
)
(
1
+
s
ω
z
2
)
(
1
+
s
ω
p
1
)
(
1
+
s
ω
p
2
)
\begin{align}G_{s}&=\cfrac{\left(\cfrac{1}{s C_{1}}+R_{2}\right) \cfrac{1}{s C_{2}} /\left(\cfrac{1}{s C_{1}}+R_{2}\right)+\cfrac{1}{s C_{2}}}{\left(\cfrac{1}{s C_{3}}+R_{3}\right) R_{1} /\left(\cfrac{1}{s C_{3}}+R_{3}\right)+R_{1}}\\ &=\cfrac{R_{2} C_{1}}{R_{1}\left(C_{1}+C_{2}\right)} \cfrac{\cfrac{1}{s R_{2} C_{1}}+1}{1+s R_{2} \cfrac{C_{1} C_{2}}{C_{1}+C_{2}}} \cfrac{s C_{3}\left(R_{1}+R_{3}\right)+1}{s R_{3} C_{3}+1}\\&=G_{0} \cfrac{\left(1+\cfrac{\omega_{\mathrm{z} 1}}{s}\right)\left(1+\cfrac{s}{\omega_{\mathrm{z} 2}}\right)}{\left(1+\cfrac{s}{\omega_{\mathrm{p} 1}}\right)\left(1+\cfrac{s}{\omega_{\mathrm{p} 2}}\right)} \end{align}
Gs=(sC31+R3)R1/(sC31+R3)+R1(sC11+R2)sC21/(sC11+R2)+sC21=R1(C1+C2)R2C11+sR2C1+C2C1C2sR2C11+1sR3C3+1sC3(R1+R3)+1=G0(1+ωp1s)(1+ωp2s)(1+sωz1)(1+ωz2s) 其中
G
0
=
R
2
R
1
C
1
C
1
+
C
2
≈
R
2
R
1
C
1
>
>
C
2
w
z
1
=
1
R
2
C
1
w
z
2
=
1
(
R
1
+
R
3
)
C
3
≈
1
R
1
C
3
R
1
>
>
R
3
w
p
1
=
1
R
2
C
1
C
2
C
1
+
C
2
≈
1
R
2
C
2
C
1
>
>
C
2
w
p
2
=
1
R
3
C
3
\begin{array}{l} G_{0}=\cfrac{R_{2}}{R_{1}} \cfrac{C_{1}}{C_{1}+C_{2}}\approx \cfrac{R_2}{R_1}\qquad C_1>> C_2\\ w_{\mathrm{z1}}=\cfrac{1}{R_{2} C_{1}} \\ w_{\mathrm{z2}}=\cfrac{1}{\left(R_{1}+R_{3}\right) C_{3}}\approx \cfrac{1}{R_1C_3} \qquad R_1>>R_3\\ w_{\mathrm{p} 1}=\cfrac{1}{R_{2} \cfrac{C_{1} C_{2}}{C_{1}+C_{2}}}\approx\cfrac{1}{R_2C_2}\qquad C_1>> C_2\\ w_{p2}=\cfrac{1}{R_3C_3} \end{array}
G0=R1R2C1+C2C1≈R1R2C1>>C2wz1=R2C11wz2=(R1+R3)C31≈R1C31R1>>R3wp1=R2C1+C2C1C21≈R2C21C1>>C2wp2=R3C31 III补偿是在II型补偿的基础上增加一对零极点来的。由此可以知道相位最大可以提升180度。显然,一个零点是由C1提供的,一个极点是由C1串C2和R2提供的。另外一个零点是由R1串R3和C3提供的,另外一个极点是由R3和C3提供的。 PI补偿和PID补偿 PI补偿(IIa型补偿)G ( s ) = K p + K i s = s K p + K i s G(s)=K_p+\cfrac{K_i}{s}=\cfrac{sK_p+K_i}{s} G(s)=Kp+sKi=ssKp+Ki PI补偿在模拟电路中又称为IIa型补偿,是II型补偿的一种,可以提供一个原点极点和一个零点,如果不需要配置高频极点的话,可以采用PI补偿。如图是PI补偿的电路形式
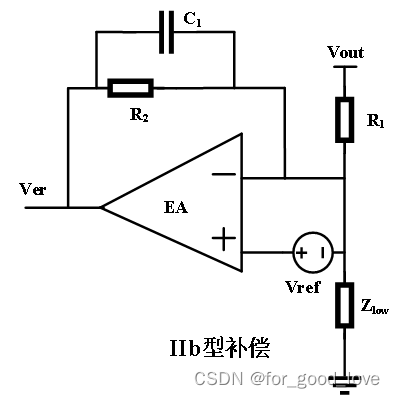
G ( s ) = 1 + s R 2 C 1 s R 1 C 1 = 1 + s w z s w p = G 0 ( 1 + w z s ) G(s)=\cfrac{1+sR_2C_1}{sR_1C_1}=\cfrac{1+\cfrac{s}{w_z}}{\cfrac{s}{w_p}}=G_0(1+\cfrac{w_z}{s}) G(s)=sR1C11+sR2C1=wps1+wzs=G0(1+swz) 显然,可以得到零点、极点、中频增益(和前面一样,改写一下形式)。 IIb型补偿IIb补偿只提供一个静态增益,在某些场合只需要比例补偿和增益衰减即可实现系统稳定,基本电路如下
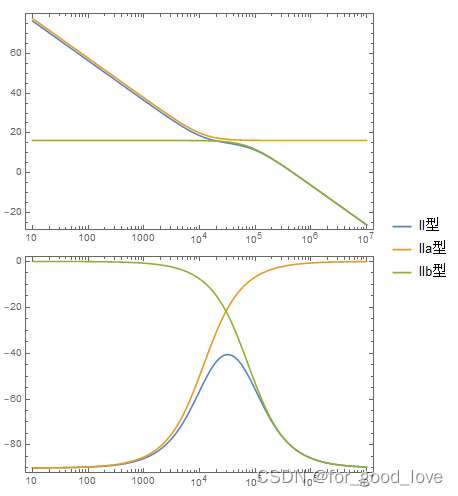
G ( s ) = R 2 R 1 1 1 + s R 2 C 1 = G 0 1 1 + s w p G(s)=\cfrac{R_2}{R_1}\cfrac{1}{1+sR_2C_1}=G_0\cfrac{1}{1+\cfrac{s}{w_p}} G(s)=R1R21+sR2C11=G01+wps1 显然可以得到高频增益为0,低频增益为G0,和极点。 下图表明了三种补偿结构的不同,低频时,IIa和II型都以-1衰减,而IIb不衰减;中频时,IIa和II转为斜率为0,IIb斜率为-1,高频时,II,IIb都以-1,IIa保持0斜率。
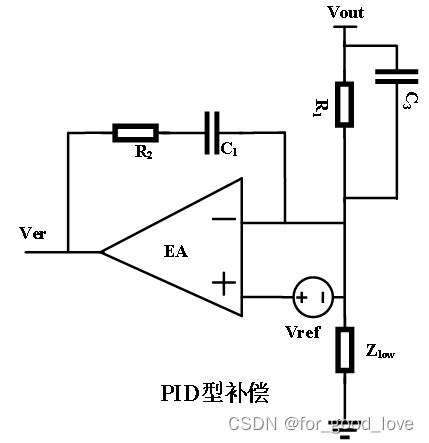
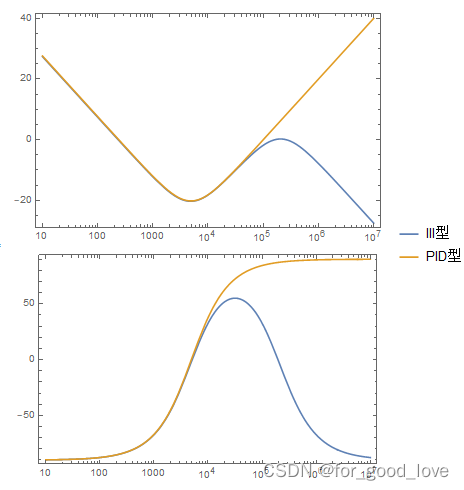
PID的基本电路形式如下,其表达式为 G ( s ) = K d s + K p + K i s = K i s 2 + K p s + K i s G(s)=K_ds+K_p+\cfrac{K_i}{s}=\cfrac{K_is^2+K_ps+K_i}{s} G(s)=Kds+Kp+sKi=sKis2+Kps+Ki 其基本模拟电路图如图,表达式为 G ( s ) = ( 1 + R 1 C 3 s ) ( 1 + C 1 R 2 s ) C 1 R 1 s = ( s + 1 C 3 R 1 ) ( s + 1 C 1 R 2 ) s C 3 R 2 G(s)=\cfrac{(1+R_1C_3s)(1+C_1R_2s)}{C_1R_1s}=\cfrac{(s+\cfrac{1}{C_3R_1})(s+\cfrac{1}{C_1R_2})}{\cfrac{s}{C_3R_2}} G(s)=C1R1s(1+R1C3s)(1+C1R2s)=C3R2s(s+C3R11)(s+C1R21)
III型补偿比PID补偿多了一个极点,同样这很好理解,分低频段、中频段和高频段去分析。由这也可以看出,PI和II型补偿不同,PID和III型补偿不同。 |
【本文地址】
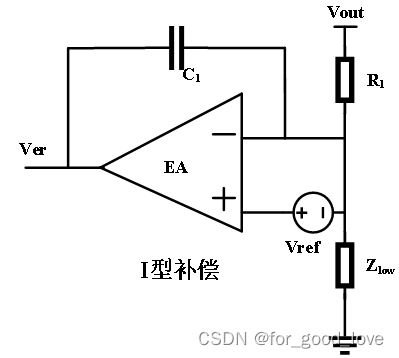 G
(
s
)
=
−
1
s
C
1
R
1
G(s)=-\cfrac{1}{s C_1R_1}
G(s)=−sC1R11
G
(
s
)
=
−
1
s
C
1
R
1
G(s)=-\cfrac{1}{s C_1R_1}
G(s)=−sC1R11