| 高级宏观与动态优化:汉密尔顿方程(Hamilton Equation) | 您所在的位置:网站首页 › 用回溯法求解哈密顿回路问题的方法 › 高级宏观与动态优化:汉密尔顿方程(Hamilton Equation) |
高级宏观与动态优化:汉密尔顿方程(Hamilton Equation)
|
这篇笔记整理最优化问题求解中的汉密尔顿方程(Hamilton Equation),之前导论提到,共有变分法、最优控制、和动态规划三种方法可以解决动态最优化问题。这篇笔记整理的汉密尔顿方程(Hamilton Equation)就是最优控制方法解决动态优化问题的一阶必要条件。 汉密尔顿方程:最优控制的一阶必要条件首先来看一下要解决的问题: 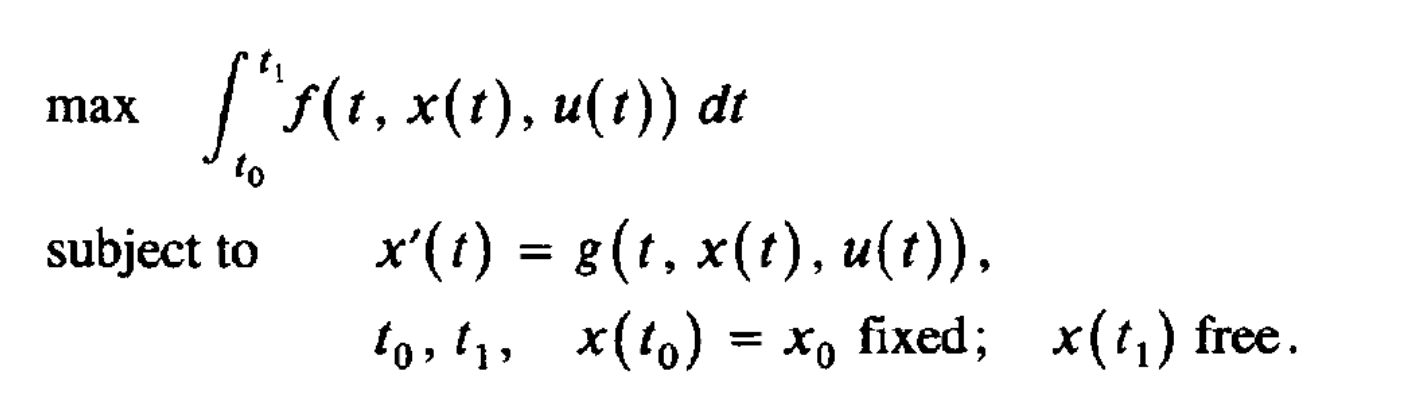 理论推导: 理论推导:令 \lambda(t) 表示一个定义在 t_0\leq t \leq t_1 上的连续可微函数,那么对于任何满足上式约束的 x(t),u(t) ,都有:  对(1)式右侧进行分部积分可得: 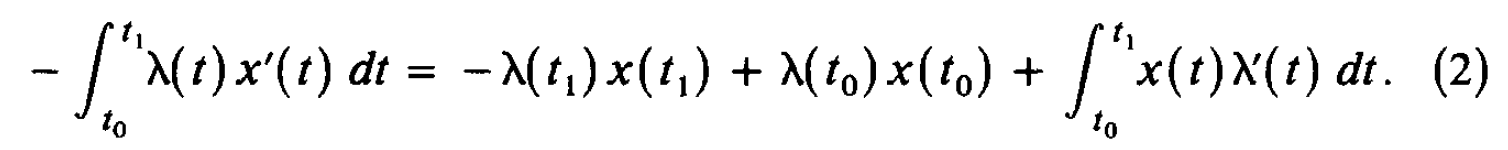 将(2)代入(1),可得: 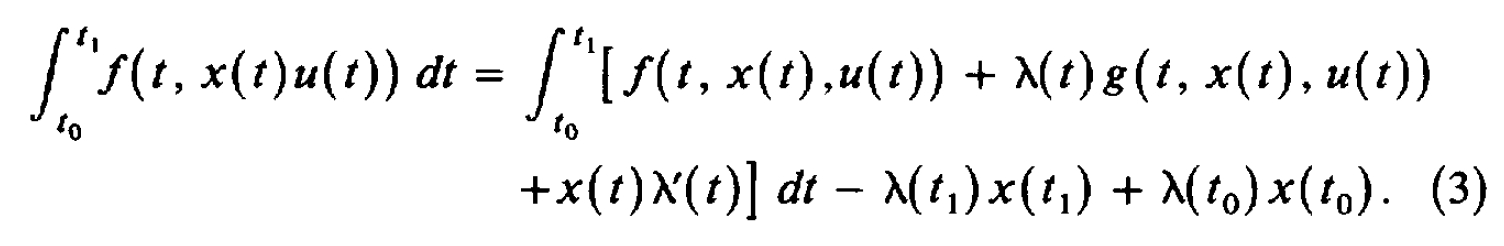 在最优控制方法中,可以发现,只要我们确定了控制变量 u(t) ,状态变量 x(t) 自然就被确定了——由那个转换方程 g 确定,因此问题的核心变为确定最优的 u^*(t)。 在变分法里面,当我们想确定下列问题的解的一阶必要条件时,我们使用的办法是在最优路径上加一个扰动,即 x^{*}(t)+ah(t), x^{*'}(t)+ah'(t) , h(t) 是 任意的但给定的。 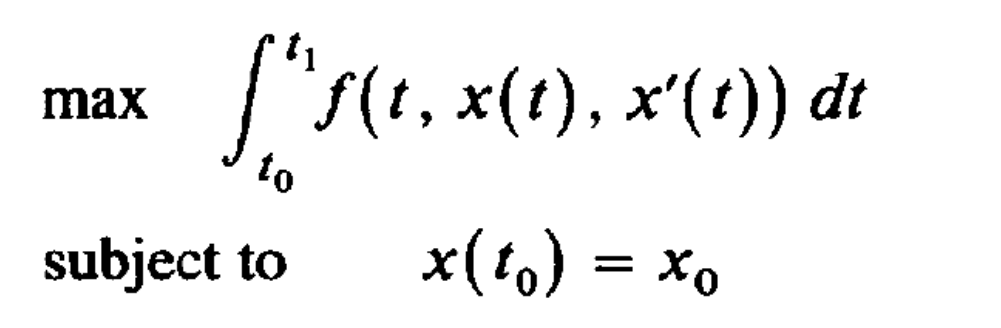 但在最优控制里面,不能这么做。因为上式可以那么做,依赖的是 x'(t)=u(t) ,但在一般化的最优控制里面,其实是: x'(t)=g(t,x(t),u(t)) ,这个时候如果设定 x(t)=x^{*}(t)+ah(t) ,我们并不知道 u(t) 和 h(t) 的关系,只能以隐函数的方式体现,因此变分法那里通过构造 x^*(t) 的扰动项 h(t) 的办法没办法适用。因此,转而构造 u(t)=u^*(t)+ah(t) 。定义 y(t,a) 为关于 u^*(t)+ah(t) 的状态变量,当然其要满足:  可以把目标函数写为:  利用(3),可以把(5)写为: 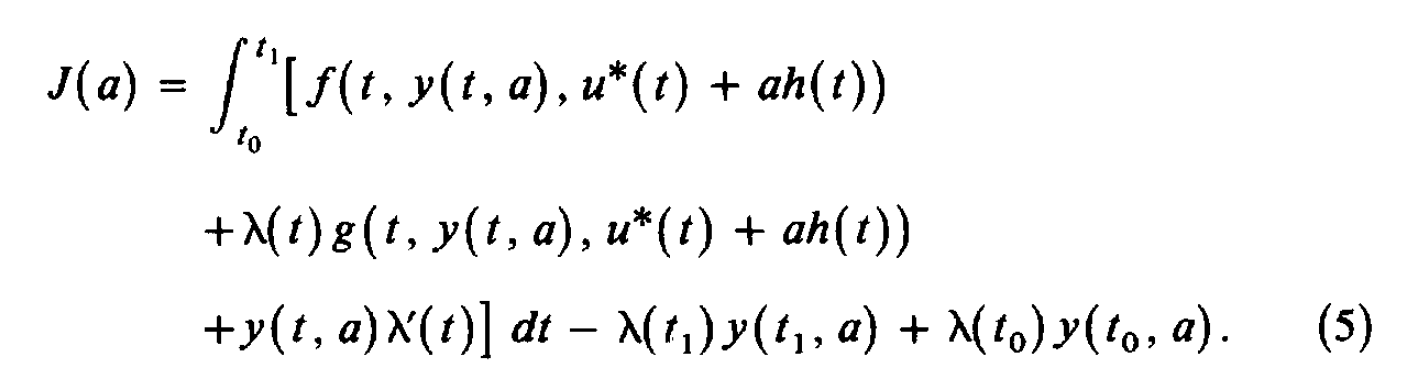 因为 u^* 是最优控制变量,因此 J(a) 在 a=0 处取得最大值,即 J'(0)=0 。  由于 y(t_0,a) 是常数,因此 y_a(t_0,0)=0 。 (6)式难以确定的是 y_a ,因为我们不知道 y(t,a) 的形式,但是可以通过构造 \lambda(t) 来消去含有 y(t,a) 的项,定义:  由此可得:  因为(8)对于任意连续 h 都成立,那么令 h=f_u(t,x^*,u^*)+\lambda(t)g_u(t,x^*,u^*) ,可得:  即:  总结一下,如果 u^*,x^* 是最优解,那么存在一个连续函数 \lambda(t) ,他们同时满足: State Equation: 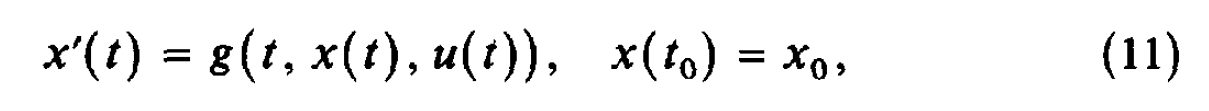 Multiplier Equation: 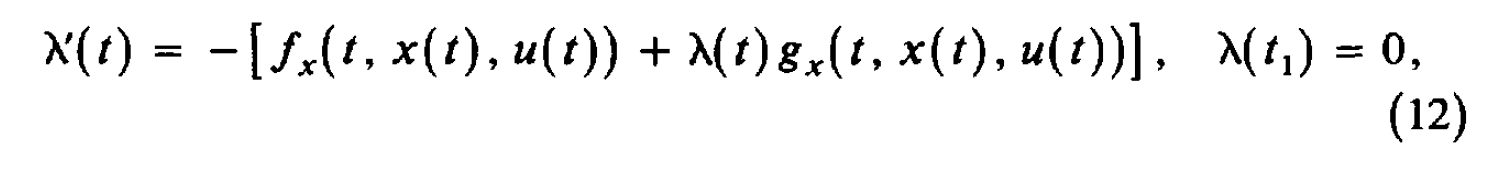 Optimality Equation:  (12) 式所表示的乘子方程也经常被称为costate, auxiliary, adjoint, or influence equation。 记忆上式的比较方便的办法是汉密尔顿方程(Hamilton Equation): 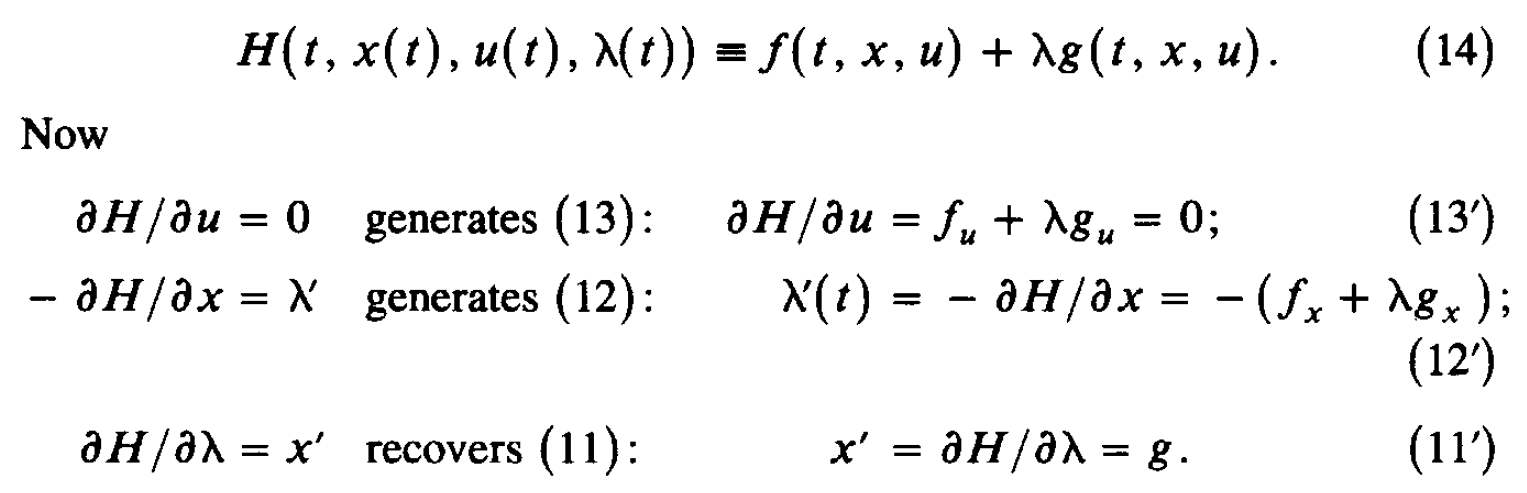 注意还有: x(t_0)=x_0,\lambda(t_1)=0 ,这两个条件经常容易忘记! 通过(13)可以把 u 表示称 x 和 \lambda 的函数,然后代入(11)和(12),得到两个微分方程,然后还有两个边界条件 x(t_0)=x_0,\lambda(t_1)=0 ,这样就可以解出来两个微分方程,从而可以求解。 注意对于最大值问题,我们还要求 H_{uu}(t,x^*,u^*,\lambda)\leq 0 ,当然对于最小值问题,则要求 H_{uu}(t,x^*,u^*,\lambda)\geq 0 。 宏观例子以后使用Optimal Control的问题,都可以使用汉密尔顿方程进行求解,来看一个例子: 例子:假设个体的即期效用函数为 u(c)=\frac{c^{1-\theta}-1}{1-\theta} ,代表性厂商有规模报酬不变的生产函数 F(K,L) ,其中 F(K,L) 具有正的且递减的边际产出。假定资本折旧率为 \delta ,假设劳动力增长率为 n 。假定单位工资收入为 w ,单位资本收入为 r 。消费者追求终身效用最大化,请推导出人均资本 k=\frac{K}{L} 和人均消费 c=\frac{C}{L} 的动态积累方程。 首先推导人均资本积累方程,首先可知,资本运动方程为: \dot{K}=F(K,L)-\delta K-C ,人均产出 f(k)=\frac{F(K,L)}{L}={F(K/L,L/L)} 。因为 {k}=\frac{K}{L} ,因此 \dot{k}=\frac{\dot{K}}{L}-\frac{K\dot{L}}{L^2}=f(k)-(n+\delta)k-c \\ 消费者追求终身效用最大化: \max_{c(t)}\int_{0}^{\infty} u(c(t))dt \\ s.t.\:\ \ \ \ \dot{k}=f(k)-(n+\delta)k-c ,\: k(0) \text{ is given}\\ 这是一个标准的最优控制问题,现值汉密尔顿方程: H=u(c)+\lambda [f(k)-(n+\delta)k-c] \\ 可得: \frac{\partial H}{\partial c}=u'(c)-\lambda=c^{-\theta}-\lambda=0 \frac{\partial H}{\partial k}=-\lambda'=\lambda[f'(k)-(n+\delta)] \frac{\partial H}{\partial \lambda}=\dot{k}=f'(k)-(n+\delta) 整理上式可得: \frac{\dot{c}}{c}=\frac{1}{\theta}[f'(k)-(n+\delta)] 求解上述两个微分方程,就可以得到人均资本和人均消费的动态运动方程。 汉密尔顿方程与欧拉方程之前我们一直学的是变分法中的欧拉方程,那么汉密尔顿方程和欧拉方程的关系是什么呢?来看下面的问题: 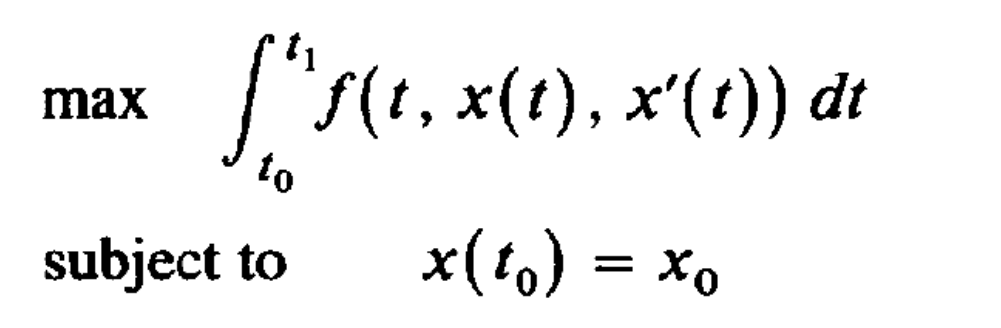 上述问题是变分法中的标准问题,可以写为一个标准的最优控制问题: 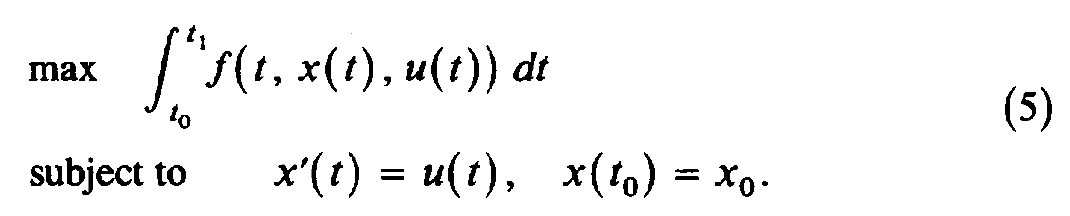 然后通过汉密尔顿方程得到一阶必要条件: \frac{\partial H}{\partial u}=f_u+\lambda=0 \frac{\partial H}{\partial x}=-\lambda '=f_x 因此可得:df_{x'}/dt=f_x ,即欧拉方程!还可以得到横截性条件: f_{x'}=0 ,当 t=t_1 时。 并且我们可以发现,二阶条件 H_{uu}(t,x^*,u^*,\lambda)\leq 0 ,等价于欧拉方程中的Legendre condition: f_{x'x'}(t,x^*,x^{'*})\leq 0 。 因此,可以发现最优控制得出来的一阶和二阶必要条件与欧拉方程是完全等价的,并且欧拉方程中的横截性条件就是最优控制中对于 \lambda(t_1) 的约束。只是从形式上来看,Euler Equation是一个二阶线性方程,而Optimal Control是两个一阶的——但二者可以相互转化。 所以这里自然会有一个巨大的疑惑,也是我之前一直在思考的问题!既然你说最优控制与变分法得到的结果是一样的,那为什么要学习最优控制呢?原因有两个:1、最优控制的适用范围更为广泛;2、在某些问题中,最优控制的经济学直觉更为清晰。 最后来看一个例子: 想要求解: 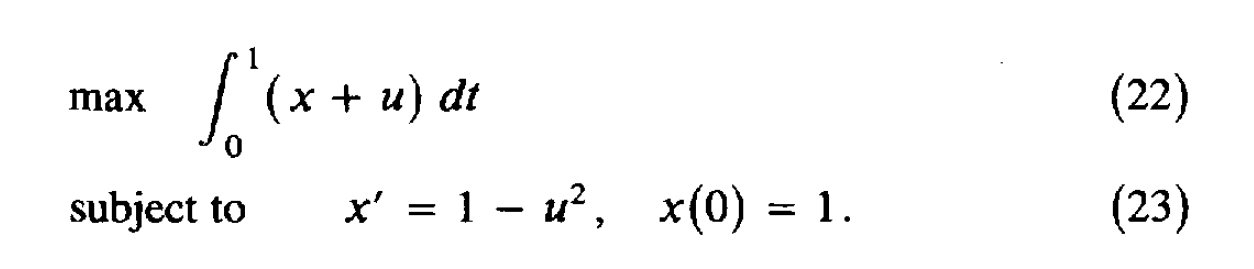 汉密尔顿方程:  先求解 \lambda(t) ,再求 u(t),x'(t),x(t) ,得到:  最优控制基本问题的一些变形 最优控制基本问题的一些变形1、如果要最优化的函数变为:  那么汉密尔顿方程的条件是不变的,只是之前的 \lambda(t_1)=0 ,此时变为了 \lambda(t_1)=\phi '(x_1) ,当然对应到欧拉方程那里,条件就变为 f_{x'}=\phi '(x_1) \text{ at } t=t_1 。 最优控制的充分条件1、函数 f 和 g 关于 x,u 均为凹函数,并且 \lambda(t)\geq 0 ,那么必要条件也是充分条件。 2、函数 f是凹函数, g 是凸函数,并且 \lambda(t)\leq 0 ,那么必要条件也是充分条件。 3、函数 f是凹函数, g 是线性函数,那么 \lambda(t) 可以任意取值。 还剩下一道习题没有想清楚:  主要是不知道 \phi(x_1) 这里应该如何处理?是要让 \phi_{x_1}(x_1^*)=0 吗? |
【本文地址】
| 今日新闻 |
| 推荐新闻 |
| 专题文章 |