| 数据挖掘概念与技术(第三版)课后答案 | 您所在的位置:网站首页 › 用python进行数据分析第二版答案 › 数据挖掘概念与技术(第三版)课后答案 |
数据挖掘概念与技术(第三版)课后答案
|
======需要原版答案请留言!!======= 2.1 再给三个用于数据散布特征的常用统计量(即未在本章讨论过的),并讨论如何在大型数据库中有效的计算它们。 1.异众比率(variation ratio):用Vr表示,其定义为:
2.2 假设所分析的的数据包括属性age,它在数据元组中的值(以递增序)为:13,15,16,16,19,20,21,22,22,25,25,25,25,30,33,33,35,35,35,35,36,40,45,46,52,70。 (a)该数的均值是多少?中位数是什么? (b)该数据的众数是什么?讨论数据的模态(即二模、三模等)。 (c)该数据的中列数是多少? (d)你能粗略的找出该数据的第一个四分位数(Q1)和第三个四分位数(Q3)吗? (e)给出该数据的五数概括。 (f)绘制该数据的盒图。 (g)分位数-分位数图与分位数图有什么区别? (a)该数的均值为 (b)该数据的众数为25和35,即该数据是一个双峰的分布,即二模。(这个数据集有两个值,它们以相同的最高频率出现,因此是双峰的) (c)该数据的中列数(数据集中最大和最小值的平均值)为(70+13)/2=41.5。 (d)第一个四分位数(相当于第25百分位)为:⌈27/4⌉=7处,Q1=20,第三个四分位数为:7∗3=21处,Q3=35。 (e)分布的五个数字汇总包括最小值、第一四分位数、中位数、第三四分位数和最大值。它很好地总结了分布的形状,这个数据是:13,20,25,35,70。 (f) (g)分位数图是一种图形方法,用于显示单变量分布中小于或等于自变量的值的近似百分比。因此,它将显示所有数据的分位数信息,其中针对自变量测量的值将相对于其相应分位数进行绘制。但是,分位数-分位数图将一个单变量分布的分位数与另一单变量分布的相应分位数作图。两个轴均显示针对其相应分布的测量值范围,并绘制对应于两个分布的分位数的点。一条线(y = x)可以与代表第一,第二和第三分位数的位置的点一起添加到图形中,以增加图形的信息价值。在同一分位数上,位于这条线上方的点表示在y轴上绘制的分布的值比在x轴上绘制的分布的值更高。相反的效果对于位于此线下方的点适用。 2.3 给定的数据集已经分组到区间,计算该数据的近似中位数。 其中,L是中位数区间的下界,N是整个数据集中值的个数,
2.4假设一家医院测试了18位随机选择的成年人的年龄和体脂数据,结果如下:
(a)计算年龄和%fat的平均值,中位数和标准差。 (b)画出年龄和%fat的盒图。 (c)根据这两个变量绘制散点图和q-q图。 (a)对于可变年龄,平均值为46.44,中位数为51,标准差为12.85。 对于变量%fat,平均值为28.78,中位数为30.7,标准偏差为8.99。 (b)
(c)
2.5 简要概述如何计算被如下属性描述的对象的相异性: (a)表称属性。 标称属性的相异性可以根据不匹配率去计算:
(b)非对称的二元属性。 非对称的二元相异性可以依据二元属性的列联表去计算,计算公式如下:
其中q是对象i和j都取1的属性数,r是在对象i中取1、在对象j中取0的属性数,s是在对象i和j都取0的属性数。 (c)数值属性。 数值属性可以有闽可夫斯基距离(Minkowski distance),它是欧几里得距离和曼哈顿距离的推广,定义如下:
其中,当h = 1时,它代表曼哈顿距离(即,L1范数);当h = 2时表示欧几里得距离(即,L2范数)。 (d)词频向量。 词频向量可以用余弦相似度与计算,其计算方式如下:
其中,余弦值0意味着两个向量呈90°夹角(正交),没有匹配。余弦值越接近于1,夹角越小,向量之间的匹配度越大。 2.6 给定两个被元组(22,1,42,10)和(20,0,36,8)表示的对象。(a)计算这两个对象之间的欧几里得距离。 (b)计算这两个对象之间的曼哈顿距离。 (c)使用q=3,计算这两个对象之间的闵可夫斯基距离。 (d)计算这两个对象之间的上确界距离。 (a)计算两个对象之间的欧几里得距离:
(b)计算两个对象之间的曼哈顿距离:
(c)使用q=3,计算这两个对象之间的闵可夫斯基距离:
(d)计算这两个对象之间的上确界距离: 2.7 中位数是数据分析中最重要的整体度量之一。提出几种中位数近似计算方法。在不同的参数设置下,分析它们各自的复杂度,并确定它们的实际近似程度。此外,提出一种启发式策略,平衡准确性与复杂性,然后把它用于你给出的所有方法。 这个问题可以在理论上或经验上都可以解决,但是做一些实验以获得结果也许更有趣。 给出了一些从不同分布采样的数据集,例如均匀分布,高斯分布,指数分布和伽玛分布。 (前两个分布是对称的,而后两个分布是偏斜的)。 例如,如果按照本章中的建议使用公式(2.3)进行近似,则最直接的方法是将所有数据划分为k个等长间隔。 其中,L是中位数区间的下界,N是整个数据集中值的个数, 显然,随着k的增大,产生的误差将减小;但是,整个过程所用的时间也会增加。误差和乘积时间的乘积是最佳的优化措施。从这一点出发,我们可以对每种类型的分布执行许多测试(这样结果就不会受到随机性的支配),并找到最佳折中方案k。 实际上,可以选择该参数值以提高系统性能。还存在其他方法来进行中值逼近。学生可以提出一些建议,分析最佳折中点,然后比较不同方法的结果。一种可能的方法如下:将整个数据集分层划分为多个区间:首先,将其划分为k个区域,然后找到中位数所在的区域;其次,将该特定区域划分为k个子区域,找到中位数所在的子区域。迭代直到子区域的宽度达到预定阈值,然后应用上述中值近似公式。这样,我们可以将中位数限制为较小的区域,而无需将所有数据全局划分为较短的时间间隔,这将很昂贵。 (成本与间隔数成正比。) 2.8 在数据分析中,重要的是选择相似性度量。然而,不存在广泛接受的主观相似性度量,结果可能因所用的相似性度量而异。虽然如此,在进行某种变换后,看来似乎不同的相似性度量可能等价。
(a)把该数据看做二位数据点。给定一个新数据点x=(1.4,1.6)作为查询点,使用欧几里得距离、上确界距离和余弦相似性,基于查询点的相似性对数据库的点排位。 (b)规格化该数据集,使得每个数据的范数等于1。在变换后的数据上使用欧几里得距离对诸数据点排位。 (a)两个n维向量x和y的欧几里得距离定义为: x和y的余弦相似度定义为: 其中
使用这些定义,我们可以获得每个点到查询点的距离。 基于欧几里得距离,排名顺序为x1,x4,x3,x5,x2。 根据余弦相似度,顺序为x1,x3,x4,x2,x5。 (b)数据单位化: 标准化数据后,我们得到:
新的欧几里得距离为:
|
【本文地址】
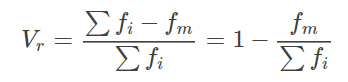 ,其中∑fi表示变量值的总频数,∑fm表示众数组的频数。异众比率主要用于衡量众数对一组数据的代表程度。异众比越大,说明非众数组的频数占总频数的比重越大,众数的代表性就越差;异众比越小,说明非众数组的频数占总频数的比重越小,众数的代表性就越好。异众比率主要适合测度分类数据的离散程度,当然,对于顺序数据与数值数据也可以进行计算。2.标准分数(standard score):变量值与其平均数的差除以标准差后的值。设标准分数为z,则有
,其中∑fi表示变量值的总频数,∑fm表示众数组的频数。异众比率主要用于衡量众数对一组数据的代表程度。异众比越大,说明非众数组的频数占总频数的比重越大,众数的代表性就越差;异众比越小,说明非众数组的频数占总频数的比重越小,众数的代表性就越好。异众比率主要适合测度分类数据的离散程度,当然,对于顺序数据与数值数据也可以进行计算。2.标准分数(standard score):变量值与其平均数的差除以标准差后的值。设标准分数为z,则有 标准分数给出了一组数据中各数值的相对位置。实际上,z分数只是将原始数据进行了线性变换,它并没有改变一个数据在该组数据中的位置,也没有改变该组数据的分布形状。3.相对离散程度:离散系数(coefficient of variation):一组数据的标准差与其相应的平均数之比称为离散系数,也称变异系数。为了消除变量值水平高低(即两个相同类型的属性其值的分布差别特别大,比如一个为几百万,而另一个为几万或几十万)和计量单位不同对离散程度测度值的影响,需要计算离散系数,其计算公式为:
标准分数给出了一组数据中各数值的相对位置。实际上,z分数只是将原始数据进行了线性变换,它并没有改变一个数据在该组数据中的位置,也没有改变该组数据的分布形状。3.相对离散程度:离散系数(coefficient of variation):一组数据的标准差与其相应的平均数之比称为离散系数,也称变异系数。为了消除变量值水平高低(即两个相同类型的属性其值的分布差别特别大,比如一个为几百万,而另一个为几万或几十万)和计量单位不同对离散程度测度值的影响,需要计算离散系数,其计算公式为: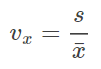 离散系数的作用主要是用于比较不同样本的离散程度。离散系数越大,说明离散程度越大。离散系数越小,说明离散程度就越小(当平均数趋于零时,离散系数就趋于无穷大,此时需要按照实际情况进行解释)。
离散系数的作用主要是用于比较不同样本的离散程度。离散系数越大,说明离散程度越大。离散系数越小,说明离散程度就越小(当平均数趋于零时,离散系数就趋于无穷大,此时需要按照实际情况进行解释)。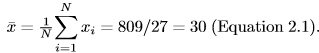 ,中位数是25(有序集合的中间值,因为集合中值的数目是奇数)。
,中位数是25(有序集合的中间值,因为集合中值的数目是奇数)。
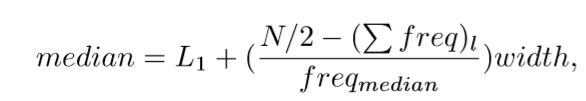








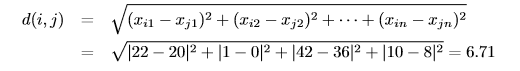





 ,
,



