组合数学

2023-08-26 16:59| 来源: 网络整理| 查看: 265

目录一写在开头1.1 本文内容二计数法则2.1 加法法则（分类加法计数）2.2 乘法法则（分步乘法计数）2.3 一一对应法则三排列与组合的定义及其计算公式3.1 排列3.2 组合四圆排列与项链排列4.1 圆排列4.2 项链排列五可重排列与可重组合5.1 可重排列5.2 可重组合六若干组合等式6.1 Stirling近似公式6.2 Pascal公式6.3 二项式定理及二项式系数6.4 多项式定理6.5 牛顿二项式定理6.6 组合恒等式七生成算法7.1 排列生成算法7.2 组合生成算法

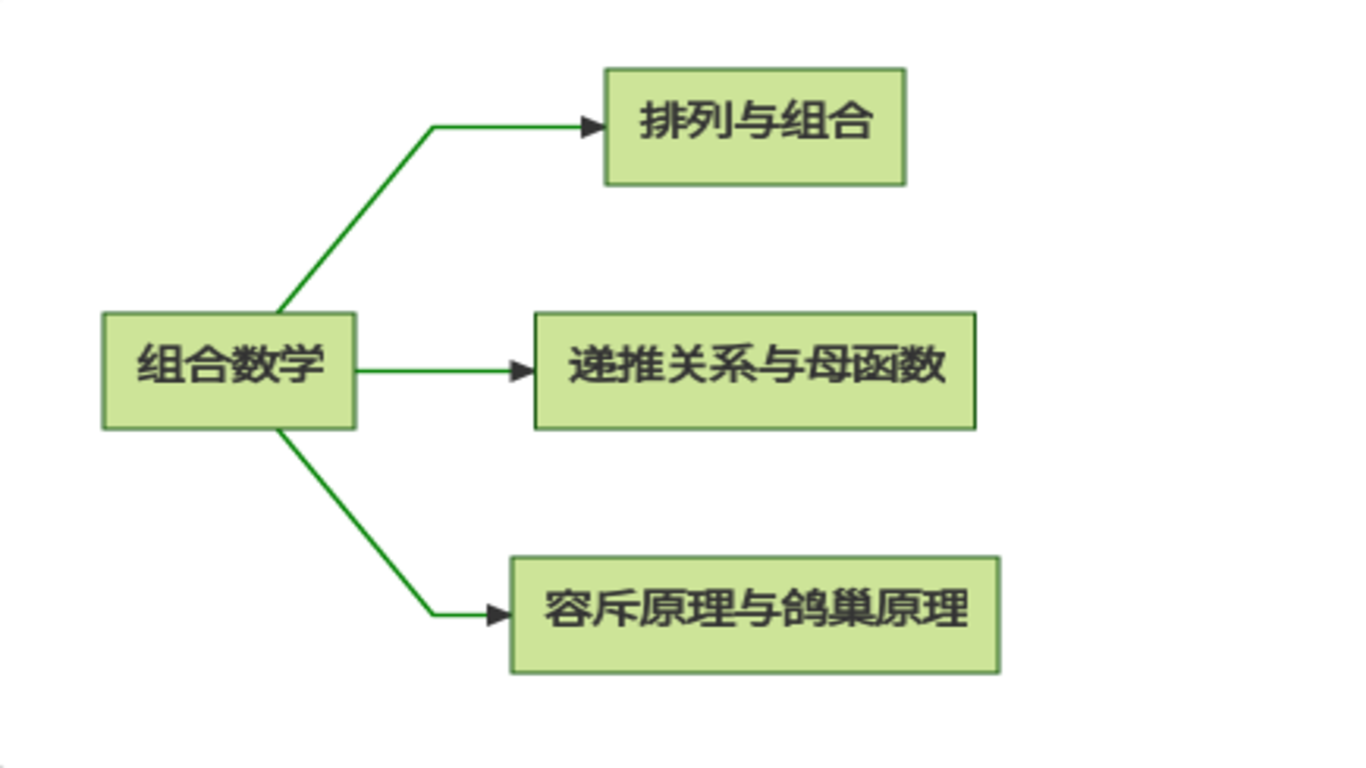
注：原创不易，转载请务必注明原作者和出处，感谢支持！

一写在开头

这个学期学习了组合数学这门课程，趁现在有时间做一下总结。整个课程的脉络如下图：

1.1 本文内容

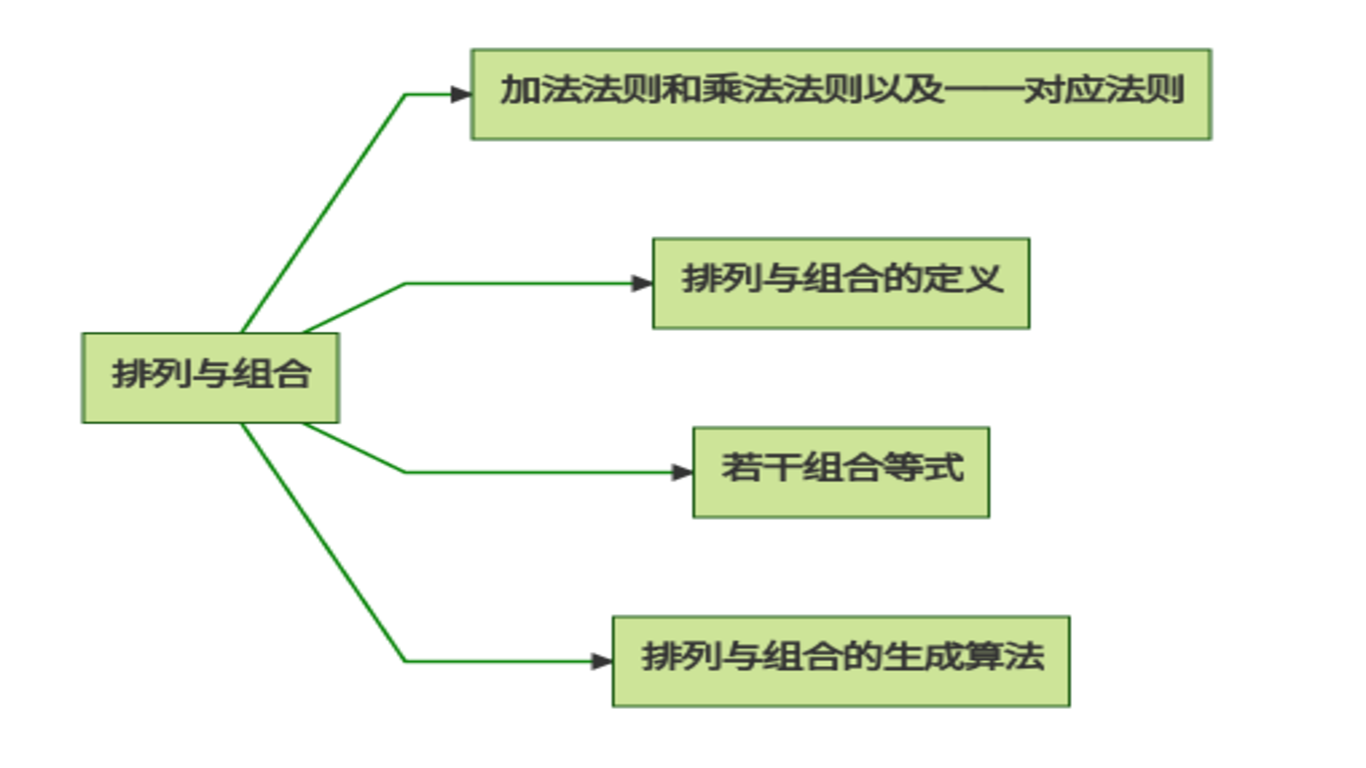
本文的内容为排列组合，内容分解图如下。

二计数法则 2.1 加法法则（分类加法计数）

假设有两个互斥的事件$A$与事件$B$，事件$A$有$m$种产生方式，事件$B$有$n$种产生方式，则事件$A$或事件$B$有$m+n$种产生方式。

2.2 乘法法则（分步乘法计数）

假设有两个相互独立的事件$A$与事件$B$，事件$A$有$m$种产生方式，事件$B$有$n$种产生方式，则事件$A$和事件$B$有$m \cdot n$种产生方式。

2.3 一一对应法则

假设事件$A$的产生方式与事件$B$的产生方式一一对应，则事件$A$的产生方式数与事件$B$产生的方式数相等。

要对$A$集合计数，但直接计数有困难，于是可设法构造一易于计数的$B$，使得$A$与$B$一一对应。

三排列与组合的定义及其计算公式 3.1 排列定义：从$n$个不同的元素中，取$r$个不重复的元素，按次序排列，称为从$n$中取$r$个的排列。排列数记为$p(n, r)$ 排列数$p(n, r)$的计算方法：相当于是从$n$个不同的球中取出$r$个，依次放入$r$个不同的盒子当中。因此，第一个盒子有$n$种选择，第二个盒子有$n-1$种选择，......，第$r$个有$n-(r-1)$种。因此可得排列数的计算公式如下：

\[\begin{equation} \begin{split} P(n, r) &= n \cdot (n-1) \cdot (n-2)......(n-r+2)(n-r+1)\\ &= n! \verb|/| (n-r)! \end{split} \end{equation} \]

特别地，当$r=n$时，称为全排列，$p(n, n)=n!$

3.2 组合定义：从$n$个不同元素中取$r$个元素，且不考虑顺序，称为从$n$个中取$r$个的组合。组合数用$c(n,r)$或者$\tbinom{n}{r}$来表示与排列不同的是，组合只是相当于从$n$个球中选择$r$个组合在一起即可，与排列相比，无需$r$个球构成一个全排列这么一个操作。因此，组合数的计算相当于是在排列数的基础上除去一个$r$的全排列$r!$即可。所以

\[\begin{equation} \begin{split} C(n,r) &= P(n, r) \verb|/| r!\\ &= n! \verb|/| \left[ (n-r)! \cdot r! \right] \end{split} \end{equation} \]

四圆排列与项链排列 4.1 圆排列定义：从$n$个不同的元素中取$r$个元素排列在一个圆环上的排列圆排列数用$Q(n,r)$来表示。因为圆排列的缘故，每$r$个首尾相连顺序一样的排列都只能算一种，如下图所示，所以，圆排列数相当于是在排列数的基础上除去$r$。所以

\[Q(n, r) = P(n, r) \verb|/| r \]

\[Q(n, n) = P(n, n) \verb|/| n = (n-1)! \]

4.2 项链排列定义：项链排列如同项链一般，在圆排列的基础上，逆时针方向和顺时针方向的放置各个数是同一个排列。因此项链排列的排列数为$Q(n, r) \verb|/| 2 = P(n, r) \verb|/| 2r$ 五可重排列与可重组合 5.1 可重排列

可重排列的定义：设有$n$种不同的物体$a_1,a_2,...,a_n$，第一种物体$a_1$有相同的$k_1$个，第二种物体$a_2$有相同的$k_2$个， ...... 第n中物体$a_n$有相同的$k_n$个，从这$n$中物品里取$r$个物品进行排列，称为$r$可重排列。

依据$r$和$k_i$的数量情况可以分为以下三种情况：

$r = k_1 + k_2 + ... + k_n$

$k_1 \ge r, k_2 \ge r, ... , k_n \ge r$或者$k_1 = \infty, k_2 = \infty, ..., k_n = \infty$

存在$k_i < r$

那么对于上述三种情况，如何计算它们的排列数呢？

对于情况1，设$S =\left \{ k_1 \cdot a_1, k_2 \cdot a_2, ..., k_n \cdot a_n\right \}$，当$k_1 + k_2 + ... + k_n = r$时，从$n$种物品中取$r$个物品的全体排列数用$P(r;k_1, k_2,...,k_n)$或$\tbinom{r}{k_1 k_2 ... k_n}$表示。则

\[P(r;k_1, k_2, ..., k_n) = r! \verb|/| (k_1 ! \cdot k_2 ! \cdot ... \cdot k_n !) \]

证明过程略

对于情况2，有

\[P(r; a_1 \cdot \infty, a_2 \cdot \infty, ..., a_n \cdot \infty) = n^r \]

证明过程略。

对于情况3，没有一个现成的公式可以计算其排列数。

5.2 可重组合

可重组合的定义：有$n$种不同的物品，构成集合$S =\left \{ k_1 \cdot a_1, k_2 \cdot a_2, ..., k_n \cdot a_n\right \}$，从这$n$种物品中取出$r$个物品的组合，称为$r$可重组合。对于可重组合可以分成以下两种特殊情况：

$k_i > r~(i = 1, 2, ..., n)$ $a_1 ,a_2, ..., a_n$至少出现一次的组合

对于情况1，有

\[C(r; a_1 \cdot \infty, a_2 \cdot \infty, ..., a_n \cdot \infty) = \tbinom{r + n - 1}{r} \]

简要证明：第1步：问题相当于$r$个相同的球放入$n$个互异的盒子，每个盒子的数目可以不同，求总的方案数

第2步：上述问题又可以转换为$r$个相同的球与$n-1$个相同的盒壁的排列问题

因此，排列数为：

\[(r+n-1)! \verb|/| (r! \cdot (n - 1)!) = \tbinom{n+r-1}{r} \]

对于情况2，$a_1 ,a_2, ..., a_n$至少出现一次的组合数为$\tbinom{r-1}{r-n}$

简要证明：因为$a_1 ,a_2, ..., a_n$至少出现一次，所以，先取出$a_1 ,a_2, ..., a_n$各一个，剩下的问题就转化为从$n$中取$r-n$个的可放回组合问题。因此，组合数为：

\[\tbinom{r-n+n-1}{r-n} = \tbinom{r-1}{r-n} \]

六若干组合等式 6.1 Stirling近似公式

Stirling公式给出了一个求$n!$的近似公式。

\[n! \approx \sqrt{2n\pi} (\frac{n}{e})^n \]

6.2 Pascal公式

\[\tbinom{n}{k} = \tbinom{n-1}{k} + \tbinom{n-1}{k-1} \]

该公式相当直观，证明也相当简单：令$S$是$n$个元素的集合，任取一个元素用$x$表示，则$S$的$k-$组合的集合可以划分为不包含$x$的$k-$组合和包含$x$的$k-$组合，于是

\[\tbinom{n}{k} = \tbinom{n-1}{k} + \tbinom{n-1}{k-1} \]

6.3 二项式定理及二项式系数

设$n$是正整数，对任意的$x$和$y$有：

\[(x+y)^n = \sum_{k=0}^n \tbinom{n}{k} x^k y^{n-k} \]

其中$\tbinom{n}{k}$为二项式系数。

根据上述二项式定理，有以下推论：

令$y=1$有：

\[(1+x)^n = \sum_{k=0}^n \tbinom{n}{k} x^k = \tbinom{n}{0} + \tbinom{n}{1}x + ... + \tbinom{n}{n}x^n \]

令$y = 1, x = -x$有：

\[(1-x)^n = \sum_{k=0}^n (-1)^k \tbinom{n}{k}x^k = \tbinom{n}{0} - \tbinom{n}{1}x + ... + \tbinom{n}{n}(-1)^k x^n \]

令$x = 1, y = 1$有：

\[\tbinom{n}{0} + \tbinom{n}{1} + ... + \tbinom{n}{n} = 2^n \]

令$x = -1, y = 1$有：

\[\tbinom{n}{0} - \tbinom{n}{1} + \tbinom{n}{2} ... + (-1)^n \tbinom{n}{n} = 0 \]

6.4 多项式定理

设$n$是正整数，则对一切实数$x_1, x_2, ..., x_m$有：

\[\begin{equation} \begin{split} (x_1 + x_2 + ... + x_m)^n &= \sum_{n_1 + n_2 + ... + n_m = n} \frac{n!}{n_1 ! \cdot n_2 ! ... n_m !}x_1^{n_1}x_2^{n_2}...x_m^{n_m}\\ &= \sum_{n_1 + n_2 + ... + n_m = n}\tbinom{n}{n_1 n_2 ... n_m}x_1^{n_1}x_2^{n_2}...x_m^{n_m} \end{split} \end{equation} \]

其中$\tbinom{n}{n_1 n_2 ... n_m}$为多项式系数。

6.5 牛顿二项式定理

设$\alpha$是一个实数。则对于所有满足$0 \leq \vert x \vert < \vert y \vert $的$x$和$y$有：

\[(x+y)^{\alpha} = \sum_{k=0}^{\infty} \tbinom{\alpha}{k} x^k y^{\alpha - k} \]

其中

\[\tbinom{\alpha}{k} = \begin{cases} 0 & k < 0\\ 1 & k = 0\\ \frac{\alpha (\alpha - 1) ... (\alpha - k + 1)}{k!} & k > 0 \end{cases} \]

6.6 组合恒等式

下面是一些组合恒等式，证明过程略。

\[\tbinom{n}{r} = \tbinom{n}{n-r} \]

\[\tbinom{n}{1}^2 + 2\tbinom{n}{2}^2 + ... + n\tbinom{n}{n}^2 = n \cdot \tbinom{2n-1}{n-1} \]

\[\tbinom{n}{r} = \tbinom{n-1}{r-1} + \tbinom{n-2}{r-1} + \tbinom{n-3}{r-1} + ... + \tbinom{r-1}{r-1} \]

\[\tbinom{n}{l}\tbinom{l}{r} = \tbinom{n}{r}\tbinom{n-r}{l-r} \neq \tbinom{n}{r} \]

\[\tbinom{n}{0} + \tbinom{n}{1} + \tbinom{n}{2} + ... + \tbinom{n}{n} = 2^n \]

\[\tbinom{m+n}{r} = \tbinom{m}{0}\tbinom{n}{r} + \tbinom{m}{1}\tbinom{n}{r-1} + ... + \tbinom{m}{r}\tbinom{n}{0} \]

\[\tbinom{n}{k} = \frac{n}{n-k}\tbinom{n-1}{k} \]

\[\tbinom{n}{k} = \frac{n-k+1}{k}\tbinom{n}{k-1} \]

\[\sum_{k=0}^m \tbinom{m}{k}\tbinom{n}{l+k} = \tbinom{m+n}{m+l} \]

七生成算法

生成算法也叫构造算法，生成算法完成的功能是将所有满足要求的排列或组合无重复，无遗漏地枚举出来

7.1 排列生成算法

排列的构造算法主要有直接法，字典序法，序列法，逆序数法，邻位对换法等等，接下来要介绍其中的一种：字典序法。

字典序法：从自然顺序123...n开始，按照字典序依次构造集合{1, 2, ..., n}的所有全排列，由一个排列构造下一个排列的算法如下：

从$p_1 p_2 ... p_n$从右向左扫描，找出比右邻数字小的第1个数字$p_i$ 对$p_1 p_2 ... p_n$从右向左扫描，找出比$p_i$大的第一个数$p_j$ 将$p_i$和$p_j$互换得到$b_1 b_2 ... b_n$ 将$b_1 b_2 ... b_n$中的$b_{i+1}$到$b_n$部分的顺序逆序，得到$b_1 b_2 ... b_n ... b_{i+1}$即为下一个排列

该算法流程很清晰，可以用C++实现如下：

void generate_permutations(vector &v, int n) { if (n < 1) return ; // 构建初始和结束排列 string first, last; for (int i = 1; i = 1; i--) if (current[i-1] < current[i]){ pi = i - 1; break; } for (i = current.length() - 1; i > pi; i--) if (current[i] > current[pi]){ pj = i; break; } // 对换 next = current; char tmp = next[pi]; next[pi] = next[pj]; next[pj] = tmp; // 翻转 for (i = pi + 1, j = next.length() - 1; i < j; i++, j--){ char tmp = next[i]; next[i] = next[j]; next[j] = tmp; } v.push_back(next); current = next; } } 7.2 组合生成算法

组合的构造算法主要有字典序法，二进制编码法等等，这里介绍前一种算法。算法的详细过程叙述如下：从{1, 2, ..., n}中取r-组合表示为$C_1 C_2 ... C_r$，令$C_1 < C_2 < ... < C_r$，其中有$C_i \leq (n-r+i), i = 1, 2, ..., r$ 则生成后续组合的规则如下

对$C_1 C_2 ... C_r$从右到左扫描，找出第一个满足$C_i < (n-r+i)$的$i$ $C_i \leftarrow C_i + 1$ $C_j \leftarrow C_{j-1} + 1, j=i+1, i+2, ..., r$

同样，上述算法可以用C++实现如下：

void generate_combinations(vector &v, int n, int r) { if ((r < 1) || (r > n)) return ; // 构建初始和结束组合 string first, last; for (int i = 0; i < r; i++){ first.push_back(char('0' + i + 1)); last.push_back(char('0' + n - r + i + 1)); } v.push_back(first); // 依次产生下一个组合并加入向量中 string next, current = first; while (current != last) { decltype(current.length()) i, j, pi; for (i = current.length() - 1; i >= 0; i--) if ((current[i] - '0') < (n - r + i + 1)){ pi = i; break; } next = current; next[pi] = next[pi] + 1; for (j = pi + 1; j < r; j++) next[j] = next[j-1] + 1; v.push_back(next); current = next; } }

【本文地址】

公司简介

联系我们