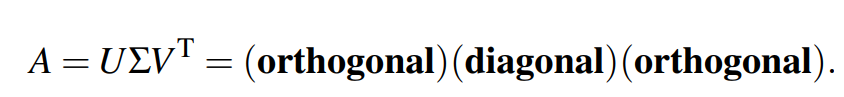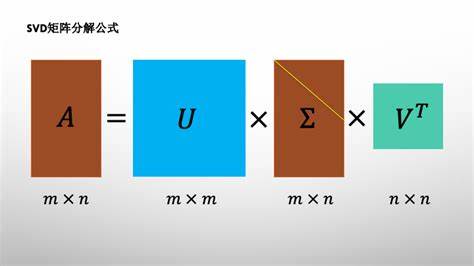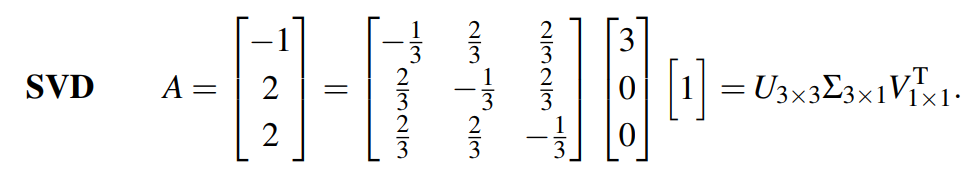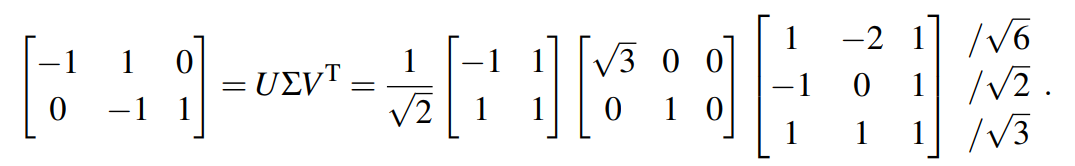设为首页收藏本站

开启辅助访问

超详细解释奇异值分解（SVD）【附例题和分析】

您所在的位置：网站首页 › 特征值求解技巧是什么 › 超详细解释奇异值分解（SVD）【附例题和分析】

超详细解释奇异值分解（SVD）【附例题和分析】

2024-06-29 14:28| 来源: 网络整理| 查看: 265

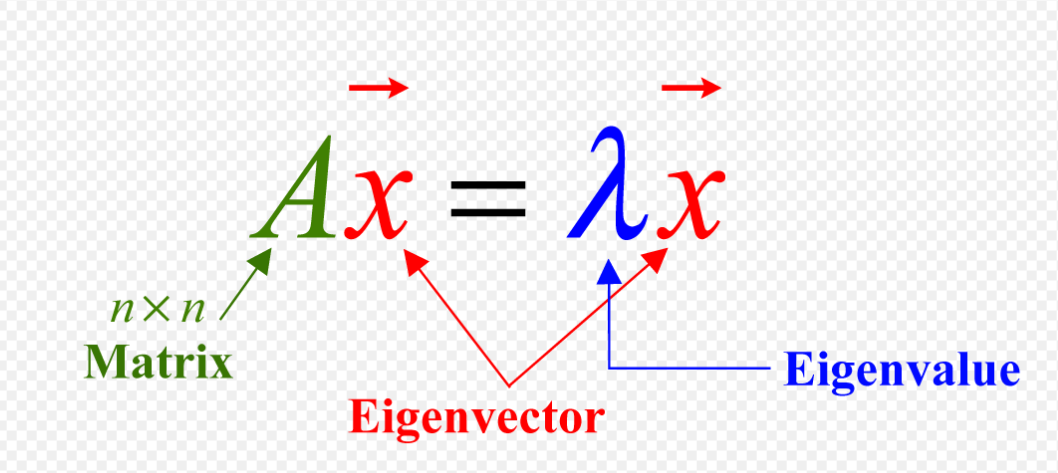
目录

一. 矩阵对角化

二. 奇异值分解

三. 对比奇异值分解与特征值分解

四. SVD分解与四大基础子空间

五. SVD分解的正交矩阵

六. 方阵与SVD分解

七. 单位特征向量与SVD分解

八. 例题分析：秩为1

九. 例题分析：秩为2

十. 计算机网络与矩阵的秩

一. 矩阵对角化

线性代数中，常出现把矩阵进行对角化的过程，然后将其应用于简化计算，解方程等等。但是，只有对称矩阵才可以对角化。另外，方阵才有特征值和特征向量的说法。

给定m行n列的矩阵A，如下方程：

$Ax=b$

该方程可能有一个解，可能有无数个解，也可能会出现无解的情况。

但我们知道 $A^TA$ 和 $AA^T$ 都是方阵，且都是半正定矩阵，所以可以对角化而且特征值都大于等于0。于是，以上方程有解：

$A^TAx=A^Tb$

二. 奇异值分解

奇异值分解，singular value decomposition，通常简写为SVD分解。

备注：建议看这部分知识的小伙伴可以先看矩阵的LU分解，QR分解。

已知正定矩阵（positive definite matrix），如果我们想分析它的特征值和特征向量，可将其分解为如下：

$Q\Lambda Q^T$

其中 $\Lambda$ 为对角矩阵，即为原始矩阵的特征值。Q为特征向量形成矩阵，如果原始矩阵为对称矩阵，矩阵Q可为标准正交矩阵，满足如下：

$QQ^T=I$

但，当矩阵非方阵（rectangular matrix），以上分解是行不通的，因为该矩阵没有特征值这一概念的。

由此，便出现了对矩阵进行SVD分解，通式如下：

$A=U\Sigma V^T$

其中 $\Sigma$ 为对角阵（非方阵），将其对角线处非零的元素记为 $\sigma_1,\cdots,\sigma_r$ ，此对角矩阵有两种理解方式：

$A^TA$ 的特征值；A的奇异值（singular value）

主对角线处的元素个数与原始矩阵A的秩有关。

备注：此处的矩阵A可以是任意矩阵，但 $A^TA$ 和 $AA^T$ 都一定为方阵。所以经常会利用这两个方阵来理解奇异值和特征值的区别。

对任意m行n列的矩阵A，奇异值分解的综合理解如下：

正交矩阵U：m行m列，该矩阵的每一个列向量都是 $AA^T$ 的特征向量；

正交矩阵V：n行n列，该矩阵的每一个列向量都是 $A^TA$ 的特征向量；

对角阵 $\Sigma$ ：m行n列，将 $A^TA$ 或 $AA^T$ 的特征值开根号，得到的就是该矩阵主对角线上的元素，也可以看成矩阵A的奇异值。

三. 对比奇异值分解与特征值分解

对于正定矩阵来讲，以上讨论的 $\Sigma$ 与 $\Lambda$ 是一样的， $U\Sigma V^T$ 与 $Q\Lambda Q^T$ 是一样的。

对于非正定矩阵（要求是对称矩阵），此时 $\Lambda$ 会出现负数，但 $\Sigma$ 依旧为正数。

推广到复数矩阵，对于SVD分解 $A=U\Sigma V^H$ ，此时的U和V即为酉矩阵（unitary），满足如下：

$U^HU=I,\quad V^HV=I$

其中， $U^H$ 和 $V^H$ 代表共轭转置。

但 $\Sigma$ 中的元素依旧为实数。

四. SVD分解与四大基础子空间

对于任意矩阵有四个非常重要的子空间：列空间（column space），行空间（row space），左零空间（left nullspace），零空间（nullspace）。

假定某m行n列矩阵A的秩为r，将矩阵U和V的列向量可以作为不同空间的标准正交基，如下：

矩阵U的前r个列向量可以作为A列空间的标准正交基；矩阵U的后m-r个列向量可以作为A左零空间的标准正交基；矩阵V的前r个列向量可以作为A行空间的标准正交基；矩阵U的后n-r个列向量可以作为A零空间的标准正交基；

如下：

五. SVD分解的正交矩阵

已知 $A=U\Sigma V^T$ ，两边同时乘以正交矩阵V，可得：

$AV=U\Sigma$

这个结果有一个很有意思的理解角度：从矩阵V中随机抽取一个列向量 $v_j$ ，对应位置抽取对角阵的元素 $\sigma_j$ ，以及矩阵U的列向量 $U_j$ ，可得：

$Av_j=u_j\sigma_j$

六. 方阵与SVD分解

对方阵 $AA^T$ 做SVD分解，如下：

$AA^T=U\Sigma V^T(U\Sigma V^T)^T=U\Sigma\Sigma^TU^T$

此时U即为 $AA^T$ 的特征向量形成的矩阵， $\Sigma\Sigma^T$ 为 $AA^T$ 的特征值。

同理，对 $A^TA$ 运算如下：

$A^TA=(U\Sigma V^T)^TU\Sigma V^T=V\Sigma^T\Sigma V^T$

此时V即为 $A^TA$ 的特征向量形成的矩阵， $\Sigma^T\Sigma$ 为 $A^TA$ 的特征值。令r代表矩阵A的秩:

$\Sigma\Sigma^T$ 为m行m列的矩阵，主对角线的元素为 $\sigma_1^2,\cdots,\sigma_r^2$ 。

$\Sigma^T\Sigma$ 为n行n列的矩阵，主对角线的元素为 $\sigma_1^2,\cdots,\sigma_r^2$ 。

可以观察到 $\Sigma^T\Sigma$ 与 $\Sigma\Sigma^T$ 都为方阵，维度是不一样的，但是它们两个主对角线元素是一模一样的。

七. 单位特征向量与SVD分解

根据“六”中的讨论， $A^TA$ 的特征值为 $\sigma_1^2,\cdots,\sigma_r^2$ ，特征向量为 $v_j$ ，由此可得：

$A^TA v_j=\sigma_j^2 v_j$

两边同时乘以矩阵A可得：

$AA^TA v_j=\sigma_j^2 Av_j$

将 $AA^T$ 看成一个矩阵， $A v_j$ 看成特征向量， $\sigma_j^2$ 看成特征值。也就是说， $A v_j$ 是矩阵 $AA^T$ 的特征向量。易得：

$||Av_j||^2=\sigma_j^2$

所以可得向量 $A v_j$ 的长度为 $\sigma_j$ ，那么可得单位向量为：

$\frac{A v_j}{\sigma_j}$

综合可得：

$\frac{A v_j}{\sigma_j}=u_j$

以上过程的本质就是 $AV=U\Sigma$

八. 例题分析：秩为1

对以下矩阵A进行SVD分解，并分析相关性质：

$A=\begin{bmatrix} -1\\ 2\\ 2 \end{bmatrix}$

解：

该矩阵仅有一列，所以秩r=1，这也就意味着该矩阵进行SVD分解，中间的对角阵 $\Sigma$ 仅有一个非零元素，如下：

对角阵 $\Sigma$ 主对角线仅有一个元素 $\sigma_1=3$ 。

易得 $A^TA$ 为1行1列的矩阵， $AA^T$ 为3行3列的矩阵，这两个矩阵都拥有特征值9，开根号后刚好为3，与以上讨论一致。

九. 例题分析：秩为2

对以下矩阵A进行SVD分解，并分析相关性质：

$A=\begin{bmatrix} -1 & 1 &0 \\ 0&-1 & 1 \end{bmatrix}$

解：

显然，矩阵A的秩为2，易运算 $AA^T$ 如下：

$AA^T=\begin{bmatrix} 2 & -1\\ -1 & 2 \end{bmatrix}$

可以分析出该方阵的特征值为3和1.

对原始矩阵A进行SVD分解如下：

可以发现该矩阵的奇异值为 $\sqrt 3$ 和 $\sqrt 1$ 。

矩阵U的每一列可以看成A的左奇异向量，也可以看成 $AA^T$ 的单位特征向量；

矩阵V的每一列可以看成A的右奇异向量，也可以看成 $A^TA$ 的单位特征向量；

十. 计算机网络与矩阵的秩

我们都知道矩阵的秩代表的是线性独立的行向量或列向量的个数。但在实际的计算中这个量不是很好分析。

在物理层安全，或无线通信中，会存在噪声，这些噪声通常很小，进而延伸出矩阵有效的秩概念。

假定 $\epsilon$ 是一个很小很小的数，可以将其看成所谓的误差（roundoff error）

（1）

$\begin{bmatrix} \epsilon &2\epsilon \\ 1 & 2 \end{bmatrix}$

很明显这个矩阵的秩为1

（2）

$\begin{bmatrix} \epsilon &1 \\ 0& 0 \end{bmatrix}$

这个矩阵的秩也很好分析，为1

接下来我们来看第三个有趣的例子：

$\begin{bmatrix} \epsilon &1 \\ \epsilon &1+\epsilon \end{bmatrix}$

乍一看这个矩阵的秩为2，但实际情况真的如此吗？

我们知道 $A^TA$ 和 $AA^T$ 均为对称的方阵，并且这两个矩阵的秩与A相同。

对这两个矩阵而言，特征值开根号即为奇异值，根据这个角度不难分析刚才的矩阵A有效的秩为1（不要忘记 $\epsilon$ 为一个很小的数）。

【本文地址】

公司简介

联系我们

CopyRight 2018-2019 实验室设备网版权所有