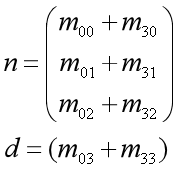视锥体剔除（Frustum Culling）算法详解

本文章介绍了如何从投影矩阵（ProjectionMatrix）推导，得到视锥体（Frustum）的六个面的面方程，并且判断一个**点（point）是否在视锥体范围内，或者包围球（Bound ing Sphere）**是否与视锥体相交。

当然，我们也可以通过ViewMatrix，将平面萃取到摄像机坐标系空间；或者通过叠加WorldModelMatrix，将平面萃取到世界坐标系空间。

课程传送门：

如果对OpenGL感兴趣的同学，可以点击下方链接，获取相关课程：

 CSDN：OpenGL从小白到精通

腾讯课堂：OpenGL从小白到精通

提示：以下是本篇文章正文内容，下面案例可供参考

首先我们考虑最简单的情况，如果给我们一个Perspective Projection Matrix（透视投影矩阵），并且同时，物体的ModelMatrix为单位阵且相机矩阵（ViewMatrix）为单位阵，那么就会如下图所示： 在这张图上，我们可以看到通过ProjectionMatrix，我们构成了六个平面，分别是top，bottom，left，right，near，far。我们的目标是：判断一个点或者一个包围球，是否在这六个面包围的空间里。

那我们就这个终极目标做一下分析：

OK，我们现在明确了我们的需求，那么就先来研究基础中的基础，平面的法线-距离表达式方程吧！

所谓平面的法线-距离表达式，直接写出来的样子如下所示：

对于这个式子，我们做一下几何上的剖析，如下图所示：

 首先我们从坐标系（看向z负方向为例）中，拿到一个向量n（且n是归一化向量），那么我接下来希望构建一个平面，这个平面与n向量垂直，那么这个平面就会有很多种选择。从图上看，平面会沿着蓝色双箭头在向量n上滑动。

那么我们定义n如下所示：

现在我们假设找到了一个平面，需要求它的平面表达式方程，如下图所示：

 那么对于蓝色平面上任意一点p，肯定都满足某种同一个的条件，下面我们来看看这个条件：

我们先将p与n做点乘，根据点乘的定义：

此时，由于n是归一化向量（注意！不要忽略），那么就会得到p在n上的投影值（两者夹角小于90度为正，大于90度为负）。那么做出来的投影绝对值，不就是平面与原点（0， 0， 0）的距离么！如下图所示： 

现在我们可以来写一写平面的方程式了，我们定义d是平面到原点的距离（可正可负），为了满足如下方程：

当d是正数，那么平面一定是从原点开始，沿着n向其反方向移动了|d|的长度；

当d是负数，那么平面一定是从原点开始，沿着n向其正方向移动了|d|的长度。

如下图所示：

 我们可以得到一个物理上的结论：

首先规定一个坐标系原点，然后从原点为起点，长出来一个向量n。随后d所代表的是，平面从零点为起点，沿着n这跟轴，向正或者反移动多少。

在得知了平面的方程式之后，如果我们在空间里随意挑选一个点，将其坐标值带入到平面的方程式，到底意味着什么东西呢？

我们首先把n这个向量当作一个数轴，坐标系的原点就是数轴的0坐标点，那么平面方程其实就是在描述任意点与归一化向量n点乘之后，在数轴上的位置与d的关系。如下图所示：

 那么我们就可以利用平面把空间分割成两个部分：一个是在平面左边；一个是在平面右边。当然，整个表达式为0，就说明在平面上。（上图所示的-d，是平面穿过数轴上的点的坐标）

我们再来欣赏一下点在n方向相同一侧（即平面正面）的情况：

 可以发现如下式子：

 同理，我们再欣赏下点在n方向相反一侧（即平面反面）的情况：

 可以发现如下式子：

 ok！我们现在得到了一个重要结论，将任一点带入到平面的方程式，如果我们得到一个非0值，那么这个值就是点到平面的距离（可正可负）。如果这个距离为正，则与n同侧；如果这个距离为负，则与n不同侧。

如果我们得到了一个面的法线-距离的表达式，那么我们通过将任意一点的坐标值带入，就可以得到一个数字，这个数字就是点到平面的距离（可正可负）。如果是正数，就位于平面正面；如果是负数，就位于平面反面。

我们接下来的目标，就是使用projectionMatrix来构建这视锥体平面的方程表达式。

首先我们来回顾下，透视投影矩阵的用处是什么。利用透视投影矩阵与某个点（p）的齐次坐标相乘，我们可以得到一个半NDC坐标（），即还没有除以w的NDC坐标。

令的xyz坐标同时除以w之后，我们就得到了NDC坐标（p_ndc)，那么在OpenGL的NDC坐标标准下，p_ndc的xyz三个值都应该是在-1到1之间，即：

然后我们把点与透视投影矩阵相乘的形式，也给写出来：

 此时我们得到的还并不是NDC坐标，所以我们需要除以最后的w值，从而得到NDC，如下：

现在我们得到了NDC坐标的表达式，由于所有坐标都必须在-1到1之间才能算作在视锥体范围内。

那么我们就可以先考查下最左边的视锥体平面，如果这个点直接在视锥体的内部，那么在NDC坐标中，它的x一定是大于-1的，我们可以得到：

 可以看到，我们得到了一个平面的方程，其中平面方程系数如下：

 从目前的条件来看，方程计算结果如果大于零，那么这个点就会位于视锥体左平面之内，根据我们之前的结论：

如果这个距离为正，则与n同侧；如果这个距离为负，则与n不同侧。

我们可以得出一个结论：本平面方程法向量是指向视锥体内侧的，并且点位于本平面正面的话，就可以在这个面的检测中，认为是在视锥体内。随后我们对其他面也应用同样的手段，如果全部通过，则认为点在视锥体范围之内，从而不会剪裁！

但是，我们还没有结束，如果看一下视锥体的右侧面（即与前面所述相反的面），就会发现有所不同。如果对右侧面进行检测，则NDC坐标的x值必须小于1，我们可以得到如下式子：

 我们会发现，这个式子判定的方法是带入的结果小于零才算做通过检测，这样的话不利于我们的代码写作，所以我们可以把判别式两边都乘以-1，就可以得到：

 好了，这样的条件我们就很舒服了，所以我们必须将判别式们都统一成为大于零才通过检测的方式。接下来，我们就可以列出来所有的六个平面的表达式：

左面：

 右面：

 上面：

下面：

 近面：

 远面：

 在一个循环当中，对这六个表达式进行判别，如果全部通过，则认为是在Frustum以内。

我们现在引入一个例子，即包围球与视锥体的相交判断。我们直到包围球有两个关键变量，一个是球心坐标center，一个是半径radius。

我们对这件事的研究，用到了我们第二节所用的观察方法，即将平面的法向量n看作是从坐标原点伸出来的一个轴，我们所有的数值研究都放在这个轴上进行。如下所示：

 图中零点在n的起点，竖直虚线表示面 

我们可以先在d>0的情况下观察，左边是球在平面反面；右边是球在平面正面。在正面的基本就不用再看，肯定通过了检测。但是我们观察左图，如果球的半径再大一些，还是有机会与平面产生相交从而通过检测的，所以我们不能单单看球心是否在平面的正面。如下图所示：

图中零点在n的起点，竖直虚线表示面  

图中，x+d不就是将球心center带入到平面方程后得到的距离值么，在上图的情况下，这个结果是负数，所以我们加了绝对值号。如果|x+d|>r，我们就会看到球的一部分已经跑到了平面的正面，所以这个球就可以不被剔除了，做成表达式如下所示：

 即满足了这个条件，就可以判定球通过了检测。那么如果球心本来就在平面的正面呢？是否也满足呢？如下图所示：

图中零点在n的起点，竖直虚线表示面  

 我们发现，x+d直接大于零，那么也肯定大于-r，所以这两种情况下，上述判别式都可以使用。我们接下来检查下d