共轭梯度法解求解大规模稀疏矩阵，对比最速梯度法（C++）

记录计算方法大作业，练习C++，欢迎指正。

共轭梯度法（Conjugate Gradient）是介于最速下降法与牛顿法之间的一个方法，它仅需利用一阶导数信息，但克服了最速下降法收敛慢的缺点，又避免了牛顿法需要存储和计算Hesse矩阵并求逆的缺点。共轭梯度法不仅是解决大型线性方程组最有用的方法之一，也是解大型非线性最优化最有效的算法之一。

在实际应用中，共轭梯度法不仅可以去求解方程组，还可以推广到非二次目标函数的极小值求解。在各种优化算法中，共轭梯度法是非常重要的一种。其优点是所需存储量小，具有步收敛性，稳定性高，而且不需要任何外来参数。

求解 Ax=b时，最简单粗暴的方式为 x=A-1 *b。但是这种方法的问题很明显：矩阵求逆的计算复杂度非常高。即使我们考虑用矩阵分解的方式，仍然会很慢。 因此，我们尽可能考虑用迭代的方式，而不是直接求逆的方式来解这个问题。如果构造一个二次函数：f(x)=xT Ax/2-b T x,求其最小值，即其导数为0时正好是方程Ax=b的解。因此，我们可以将线性方程组求解问题转化为二次函数求极小值问题

在寻优过程中利用当前点xk 处的残向量rk 和前一迭代点xk-1 处的搜索方向dk-1 对搜索方向进行如下修正：

𝑑𝑘 = 𝑟𝑘 + 𝛽𝑘−1𝑑𝑘−1

其修正系数𝛽𝑘−1的取值有一个约束条件，即要确保𝑑𝑘与𝑑𝑘 , 𝑑𝑘−1 ,⋯, 𝑑0之间满足 关于 A 的共轭关系。这就是共轭梯度法的基本思想。可以看出共轭梯度法的搜 索方向𝑑𝑘的计算只需要梯度向量，不需要海森矩阵 H，可以推广到非二次目标函 数的极小值求解。

下面给出共轭梯度法求解方程组的伪代码：

(1) 给定初始近似向量𝑥 (0)以及精度𝜖 > 0;

(2) 计算𝑟 (0) = 𝑏 − 𝐴𝑥 (0)，𝑑 (0) = 𝑟 (0)；

(3) for k=0 to n-1 do

      (i) 𝛼𝑘 = 𝑟 (𝑘)𝑇𝑟 (𝑘) 𝑑(𝑘)𝑇𝐴𝑑(𝑘) ;

     (ii) 𝑥 (𝑘+1) = 𝑥 (𝑘) + 𝛼𝑘𝑑 (𝑘) ;

     (iii) 𝑟 (𝑘+1) = 𝑏 − 𝐴𝑥 (𝑘+1) ;

    (iv) 如果|| 𝑟 (𝑘+1) || < 𝜖或者 k+1=n，则输出近似解𝑥 (𝑘+1)，停止；否则转(v)

    (v) 𝛽𝑘 = || 𝑟 (𝑘+1) ||2 2 || 𝑟 (𝑘) ||2 2 ;

     (vi) 𝑑 (𝑘+1) = 𝑟 (𝑘+1) + 𝛽𝑘𝑑 (𝑘) ;

end do

本次计算的实例采用的是课本第 133 页中的例 3.2，分别分析了 n 的取值为 100，200，400 时的情况，并同时用共轭梯度法和最速下降法去求解线性方程， 设置两种方法的精度为 0.0001。

该程序只包含一个 cpp 文件。请将要求解的方程组的系数矩阵保存在对应文 件夹下的 data.txt 中。 程序中有共轭梯度法和最速下降法的函数，两种方法求得的结果和对应的迭 代 误 差 保 存 在 对 应 文 件 夹 下 的 ConjugateGradientMethod.txt 和 SteepestDescentMethod.txt 中。文件夹保存和读取的路径都放在程序开头的全局 变量中，可以自行修改。

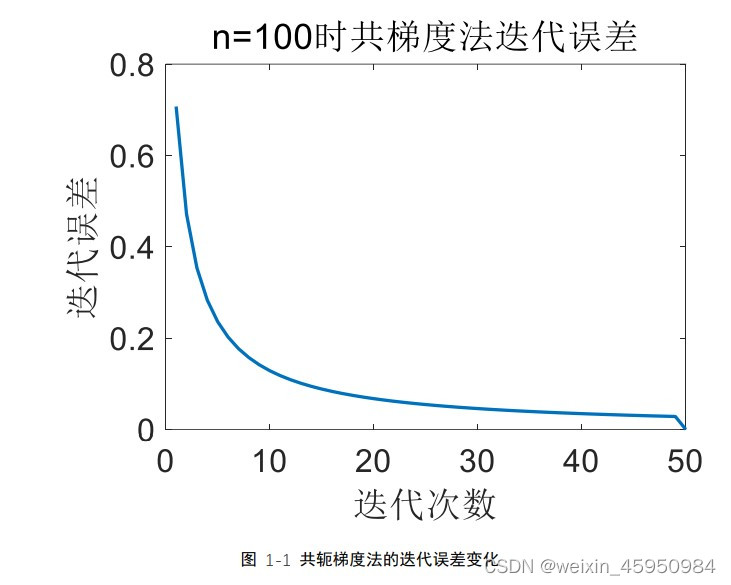
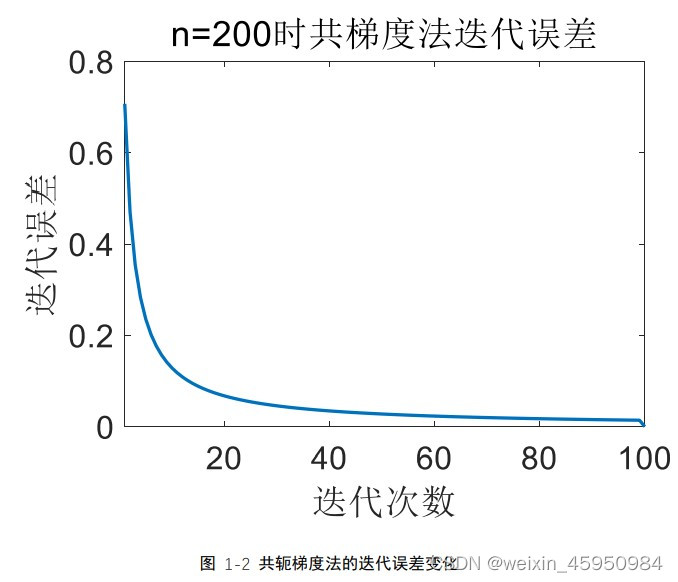
 图 1-1 共轭梯度法的迭代误差变化 图 1-1 是共轭梯度法迭代过程中的误 差变化，可以看出该方法最终收敛，且共轭梯度解出来的结果是一个全 1 的向 量，也就是所有的未知数都是 1。 通过最速下降法得到的解为[0.5,0,0,0,0,0,……,0,0,0,0.5],即 x1 和 x100 是 0.5， 其他 x 的值为 0，带入到原方程组中发现符合解特征。而且最速下降法只迭代一 次就得到最终解

（2）N=200

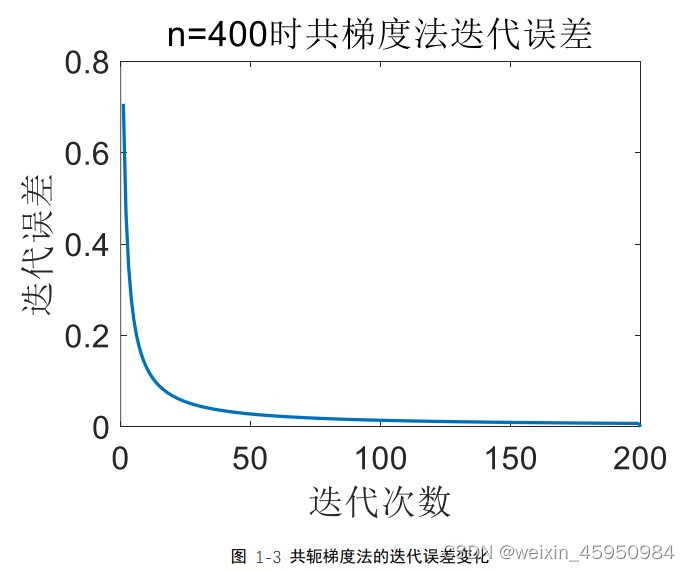
（3）N=400

（1）迭代结果

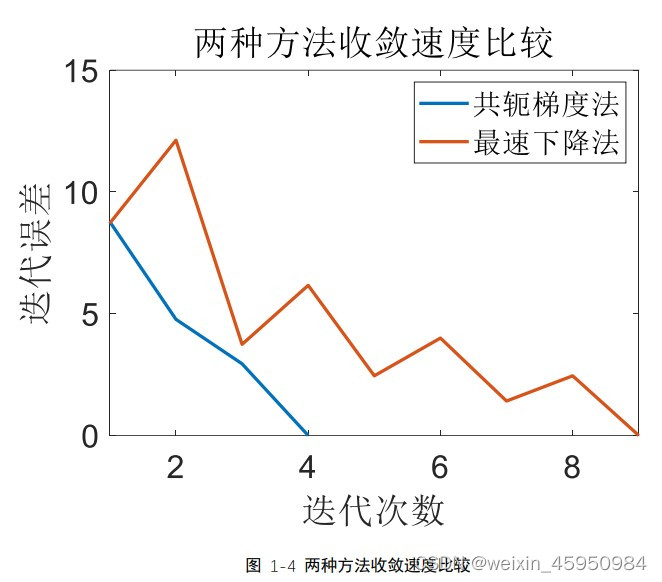
（2）迭代速度

 图 1-4 是两种方法解方程组迭代收敛的过程，可以看出共轭梯度在进行四 次迭代时就已经收敛，最速下降法在 9 次迭代之后才收敛。从迭代误差的变化 中可以发现此时梯度下降法的每次迭代的误差总是比上次小，但是最速下降法 每次迭代的误差还可能比前一次大，说明共轭梯度在每次迭代都是向着准确解 的方向移动。

最速下降法相邻两次迭代的方向是正交的，这就说明最速下降法每次迭代 的方向并不是都朝着最优解的方向，而且这种正交性会导致最速下降法向极小点逼近是曲折前进的，这种现象会影响收敛速度。同时这种迭代方式很可能使 迭代陷入局部最优解，影响优化的结果。

主函数：