【机器学习算法】基于最小二乘损失(MSE)的多元线性回归解析解推导

基于上一节的博客我们基于概率统计中最大似然估计的角度推导了多元线性回归的损失函数，但没有给出具体求解该函数的方式，在本节中我们将再次硬核一波，利用数学公式推得该损失函数的解析解形式。(至于为什么是解析解，这是因为多元线性回归其数值解基于样本的不同而不同，我们只能求出解的函数表达式，最后再通过计算机求出精确解)

线性回归损失函数： l o s s = ∑ i = 1 m ( y ( i ) − θ T x ( i ) ) 2 loss= \sum_{i=1}^{m}\left(y^{(i)}-\theta^{T} x^{(i)}\right)^{2} loss=i=1∑m​(y(i)−θTx(i))2

如果yi，xi，θ均为一元变量，就是一元线性回归。我们先来探讨下一元线性回归的解析解形式，为了区分，这里把θ换成w，其中的偏置项b也单独分离出来： 可以看到，一元线性回归的解析解其实并不那么直观，如果是多元线性回归，只要把yi，xi换成向量，θ换成矩阵即可。

由于我们在求取argmax(theta)loss时会用到求导，并且任何常数项系数不会影响theta的最终取值。所以这里我们使用一个小trick，在函数前乘上一个常数1/2，方便直接约去平方项求导产生的常数2: l o s s = 1 2 ∑ i = 1 m ( y ( i ) − θ T x ( i ) ) 2 loss= \frac{1}{2} \sum_{i=1}^{m}\left(y^{(i)}-\theta^{T} x^{(i)}\right)^{2} loss=21​i=1∑m​(y(i)−θTx(i))2

转化为矩阵运算的简洁形式：

l o s s = 1 2 ( θ T X − y ) T ( θ T X − y ) = 1 2 ( ( X θ ) T − y T ) ( X θ − y ) = 1 2 ( θ T X T − y T ) ( X θ − y ) = 1 2 ( θ T X T X θ − θ T X T y − y T X θ + y T y ) \begin{aligned} &loss=\frac{1}{2}(\theta^{T}X-y)^{T}(\theta^{T}X-y) \\ &=\frac{1}{2}\left((X \theta)^{T}-y^{T}\right)(X \theta-y) \\ &=\frac{1}{2}\left(\theta^{T} X^{T}-y^{T}\right)(X \theta-y) \\ &=\frac{1}{2}\left(\theta^{T} X^{T} X \theta-\theta^{T} X^{T} y-y^{T} X \theta+y^{T} y\right) \end{aligned} ​loss=21​(θTX−y)T(θTX−y)=21​((Xθ)T−yT)(Xθ−y)=21​(θTXT−yT)(Xθ−y)=21​(θTXTXθ−θTXTy−yTXθ+yTy)​ 这里需要注意一点就是： θ T X 和 X θ \begin{aligned} \theta^{T}X 和 X \theta \end{aligned} θTX和Xθ​ 上述的两个形式都可以原来描述多元线性回归表达式，只不过需要注意的一点就是左边的X中的每一条样本是以列向量的形式存在的，一般用于描述在样本只有一条的情况下，而右边的X中的每条样本是以行向量的形式存在的，在X包含多条样本的时候，我们比较常使用第二种表示形式：

多元线性函数同一元线性函数一样，函数的最优解一定对应于函数之中的一个极值点，在一元线性函数中，求解函数的极值点就是判断这个函数的一阶导是否为0，扩展到多元函数上，即对应这个函数的梯度为0：

首先给出矩阵常用的求导公式： ∂ θ T A θ ∂ θ = 2 A θ ∂ θ T A ∂ θ = A ∂ A θ ∂ θ = A T \begin{aligned} &\frac{\partial \theta^{T} A \theta}{\partial \theta}=2 A \theta \\ &\frac{\partial \theta^{T} A}{\partial \theta}=A \\ &\frac{\partial A \theta}{\partial \theta}=A^{T} \end{aligned} ​∂θ∂θTAθ​=2Aθ∂θ∂θTA​=A∂θ∂Aθ​=AT​ 因此有 l o s s ′ ( θ ) = 1 2 [ ( θ T X T X θ ) ′ − ( θ T X T y ) ′ − ( y T X θ ) ′ + ( y T y ) ′ ] = 1 2 [ 2 X T X θ − X T y − ( y T X ) T ] = 1 2 [ 2 X T X θ − 2 X T y ] = X T X θ − X T y = X T ( X θ − y ) \begin{aligned} loss^{\prime}(\theta) &=\frac{1}{2}\left[\left(\theta^{T} X^{T} X \theta\right)^{\prime}-\left(\theta^{T} X^{T} y\right)^{\prime}-\left(y^{T} X \theta\right)^{\prime}+\left(y^{T} y\right)^{\prime}\right] \\ &=\frac{1}{2}\left[2 X^{T} X \theta-X^{T} y-\left(y^{T} X\right)^{T}\right] \\ &=\frac{1}{2}\left[2 X^{T} X \theta-2 X^{T} y\right] \\ &=X^{T} X \theta-X^{T} y\\ &=X^{T}(X \theta-y) \end{aligned} loss′(θ)​=21​[(θTXTXθ)′−(θTXTy)′−(yTXθ)′+(yTy)′]=21​[2XTXθ−XTy−(yTX)T]=21​[2XTXθ−2XTy]=XTXθ−XTy=XT(Xθ−y)​ 根据极值点的导数为0，因此： X T X θ − X T y = 0 θ = ( X T X ) − 1 X T y X^{T} X \theta-X^{T} y =0 \\ \theta=\left(X^{T} X\right)^{-1} X^{T} y XTXθ−XTy=0θ=(XTX)−1XTy 最终我们便得到当损失函数取得最小值时theta的解析解形式。大功告成，只需要将原始数据中的输入x与标签y作为解析解中的参数，求得的theta一定能使loss达到最小，，吗

这时候可能就有人产生疑惑了，不对，你这有问题呀，我们所求得的theta只能代表loss函数取得极值点的值，极值点也有可能是是极大值点呀，即使是极小值点，也不一定是全局最优的那个极小值点呀，这样一来，你这个推导的前提就已经靠不住脚了。

是的。。。没错，这位同学说得对呀，我们单凭一阶导为0的确不能判断一个函数在该点具有极小值，更不能判断函数在该点具有最小值。

在一元函数中，我们知道，函数的极大值或极小值点可以通过二阶导判断，极大值点处的二阶导大于0，极小值点处的二阶导小于0，对于多元函数，情况稍微比较复杂，不过判别方法也是类似的。

在多元函数中，函数的二阶导可以通过**黑塞矩阵(Hessian Matrix)**表示。黑塞矩阵是有目标函数某点处的二阶偏导所构成的对称矩阵，具体形式如下：

H ( f ) = [ ∂ 2 f ∂ x 1 2 ∂ 2 f ∂ x 1 ∂ x 2 ⋯ ∂ 2 f ∂ x 1 ∂ x n ∂ 2 f ∂ x 2 ∂ x 1 ∂ 2 f ∂ x 2 2 ⋯ ∂ 2 f ∂ x 2 ∂ x n ⋮ ⋮ ⋱ ⋮ ∂ 2 f ∂ x n ∂ x 1 ∂ 2 f ∂ x n ∂ x 2 ⋯ ∂ 2 f ∂ x n 2 ] = ( ∂ 2 f ∂ x i ∂ x j ) H(f)=\left[\begin{array}{cccc} \frac{\partial^{2} f}{\partial x_{1}^{2}} & \frac{\partial^{2} f}{\partial x_{1} \partial x_{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{1} \partial x_{n}} \\ \frac{\partial^{2} f}{\partial x_{2} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{2}^{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{2} \partial x_{n}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^{2} f}{\partial x_{n} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{n} \partial x_{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{n}^{2}} \end{array}\right] =\left(\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}}\right) H(f)=⎣⎢⎢⎢⎢⎢⎡​∂x12​∂2f​∂x2​∂x1​∂2f​⋮∂xn​∂x1​∂2f​​∂x1​∂x2​∂2f​∂x22​∂2f​⋮∂xn​∂x2​∂2f​​⋯⋯⋱⋯​∂x1​∂xn​∂2f​∂x2​∂xn​∂2f​⋮∂xn2​∂2f​​⎦⎥⎥⎥⎥⎥⎤​=(∂xi​∂xj​∂2f​) 黑塞矩阵不仅能用来判断函数的极值点类型，还能用来判断函数的凹凸性，而函数的凹凸性对于求解像多元函数回归这样的最优化问题是十分必要的。

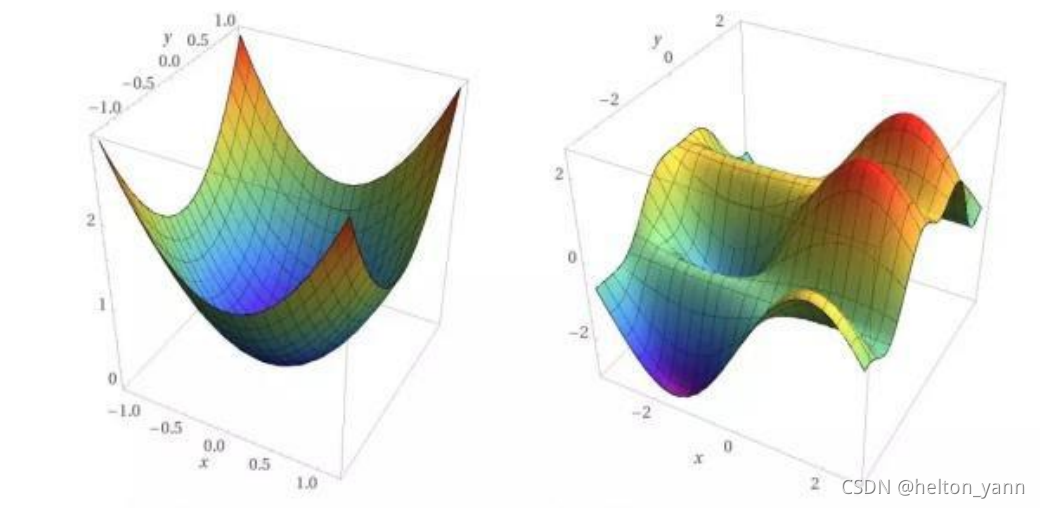
直观理解

凸函数:(若函数有极值，则是极小值，且是全局最小值)

非凸函数:(函数的极值有多个或有鞍点)

在机器学习中，若一个优化问题的损失函数是凸函数，则说明该函数的极值点一定是极小值点且一定是全局最优解，这样一来，我们通过解析解或将来使用梯度下降法迭代优化收敛得到的值，就一定会是全局最优解。

而判断函数凹凸性的一个方法就是看这个函数的黑塞矩阵是否是半正定的。

对称矩阵正负定的定义：

正定 对于实对称矩阵M,任意非0实系数向量x，有xᵀMx>0

半正定对于实对称矩阵M,任意非0实系数向量x，有xᵀMx≥0

负定 对于实对称矩阵M,任意非0实系数向量x，有xᵀMx