统计学名词解释

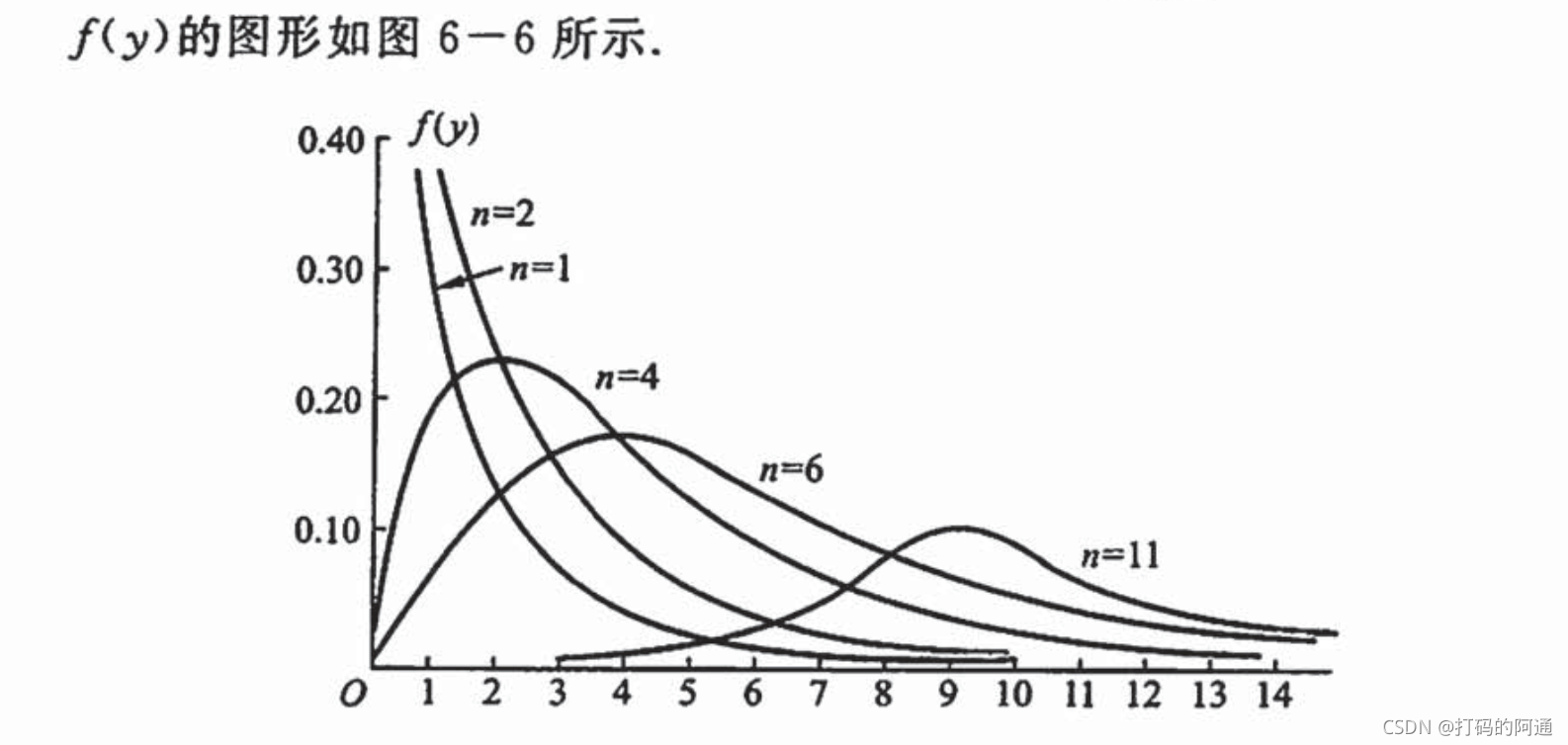
从经验可知，大部分的样本分布服从或近似服从「正态分布」。现在我们要看看和正态分布有所异同，也是非常常见的三大分布都是什么样的。

Y ∼ X 2 ( n ) Y \sim X^2(n) Y∼X2(n) 分布又称卡方分布，它的定义如下：

设 X 1 , X 2 , ⋯   , X n X_1, X_2, \cdots, X_n X1​,X2​,⋯,Xn​ 来自正态分布总体 N ( 0 , 1 ) N(0, 1) N(0,1) 的样本，则称统计量

Y = X 1 2 + X 2 2 + ⋯ X n 2 Y = X_1^2 + X_2^2 + \cdots X_n^2 Y=X12​+X22​+⋯Xn2​

服从自由度为 n n n 的 X 2 X^2 X2 分布，记为 Y ∼ X 2 ( n ) Y \sim X^2(n) Y∼X2(n)， X 2 ( n ) X^2(n) X2(n) 分布的概率密度函数为：

f ( y ) = { 1 2 n / 2 Γ ( n / 2 ) y n / 2 − 1 e − y / 2 y > 0 0 o t h e r w i s e f(y) = \left \{ \begin{matrix} \frac{1}{2^{n/2} \Gamma (n / 2)} y^{n/2-1} e^{-y / 2} & y > 0 \\ 0 & otherwise \end{matrix} \right . f(y)={2n/2Γ(n/2)1​yn/2−1e−y/20​y>0otherwise​

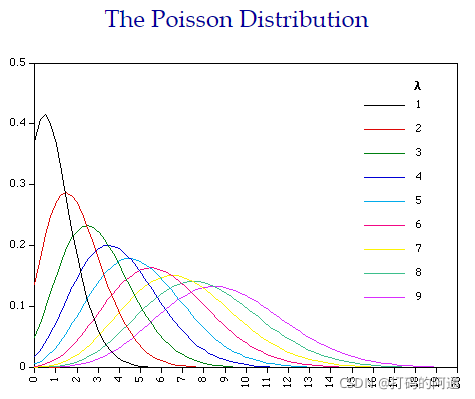
这张图主要说明，随着样本数增加，卡方分布的概率密度图像逐渐从类似 l o g log log 的对数图像逐渐接近柏松分布。使得「概率密度图像（PDF）」呈现出和「泊松等待」相类似的特征。 由于组成卡方分布的每个样本 X X X 来自标准正态分布，所以每个独立样本的期望 E ( X ) = 0 E(X) = 0 E(X)=0，方差 D ( X ) = 1 D(X) = 1 D(X)=1。

对于 X 2 X^2 X2 分布来说它有两个性质

其一：

当 X 2 X^2 X2 分布的期望 E ( Y ) = n E(Y) = n E(Y)=n时，它的方差 D ( Y ) = 2 n D(Y) = 2n D(Y)=2n

其二：

X 2 X^2 X2 分布具有可加性。 比如，有 X ∼ Y 2 ( m ) X \sim Y^2(m) X∼Y2(m) 和 Y ∼ Y 2 ( n ) Y \sim Y^2(n) Y∼Y2(n)，且 X 和 Y 相互独立，有 X + Y ∼ X 2 ( m + n ) X+Y \sim X^2(m+n) X+Y∼X2(m+n)

设 ( X 1 , X 2 , ⋯   , X 6 ) (X_1, X_2, \cdots, X_6) (X1​,X2​,⋯,X6​) 为取自标准正态总体 N ( 0 , 1 ) N(0, 1) N(0,1) 的一个样本，求下列三个统计量的分布 （1） X 1 2 + X 2 2 X_1^2 + X_2^2 X12​+X22​ （2） X 1 2 X_1^2 X12​ （3） X 1 2 + a ( X 2 + X 3 ) 2 + b ( X 4 + X 5 + X 6 ) 2 X_1^2 + a(X_2 + X_3)^2 + b(X_4 + X_5 + X_6)^2 X12​+a(X2​+X3​)2+b(X4​+X5​+X6​)2

解（1）： 由样本定义可知， X 1 , X 2 , ⋯ X 6 X_1, X_2, \cdots X_6 X1​,X2​,⋯X6​ 彼此相互独立，且服从 N ( 0 , 1 ) N(0,1) N(0,1)，所以 X 1 2 + X 2 2 ∼ X 2 ( 2 ) X_1^2 + X_2^2 \sim X^2(2) X12​+X22​∼X2(2)

解（2）： 由样本定义可知， X 1 , X 2 , ⋯ X 6 X_1, X_2, \cdots X_6 X1​,X2​,⋯X6​ 彼此相互独立，且服从 N ( 0 , 1 ) N(0,1) N(0,1)，因此对于单个元素它的卡方分布为 X 1 2 ∼ X 2 ( 1 ) X_1^2 \sim X^2(1) X12​∼X2(1)

解（3）： 从卡方分布的定义出发，我们令

Y 1 = X 1 2 Y 2 = a ( X 2 + X 3 ) 2 Y 3 = b ( X 4 + X 5 + X 6 ) 2 Y_1 = X_1^2 \\ Y_2 = a(X_2 + X_3)^2 \\ Y_3 = b(X_4 + X_5 + X_6)^2 Y1​=X12​Y2​=a(X2​+X3​)2Y3​=b(X4​+X5​+X6​)2

对于 Y 1 = X 1 2 Y_1 = X_1^2 Y1​=X12​来说，由于元素来自标准正态总体，所以 Y 1 Y_1 Y1​ 的期望 E ( Y 1 ) = 0 E(Y_1) = 0 E(Y1​)=0，方差 D ( Y 1 ) = 1 D(Y_1) = 1 D(Y1​)=1，所以 Y 1 ∼ N ( 0 , 1 ) Y_1 \sim N(0, 1) Y1​∼N(0,1)

对于 Y 2 = a ( X 2 + X 3 ) 2 Y_2 = a(X_2 + X_3)^2 Y2​=a(X2​+X3​)2 来说，它有两个离散的样本，在 《概率论基础 —— 8.数学期望、方差、协方差》 一节中，我们可以知道由样本 ( X 2 , X 3 ) (X_2, X_3) (X2​,X3​) 组成的离散集合，我们可以通过离散型期望、方差的计算方法得到 E ( X 2 , X 3 ) = E ( X 2 ) + E ( X 3 ) = 0 E(X_2, X_3) = E(X_2) + E(X_3) = 0 E(X2​,X3​)=E(X2​)+E(X3​)=0，其方差 D ( X 2 , X 3 ) = D ( X 2 ) + D ( X 3 ) = 2 D(X_2, X_3) = D(X_2) +D(X_3) = 2 D(X2​,X3​)=D(X2​)+D(X3​)=2，于是有 ( X 2 + X 3 ) ∼ N ( 0 , 2 ) (X_2 + X_3) \sim N(0, 2) (X2​+X3​)∼N(0,2) ，我们对正太分布进行标准化，代入如下公式：

X − μ σ = X − 0 2 = X 2 \frac{X - \mu}{\sigma} = \frac{X - 0}{\sqrt{2}} = \frac{X}{\sqrt 2} σX−μ​=2 ​X−0​=2 ​X​

于是我们得到标准正态分布 X 2 + X 3 2 ∼ N ( 0 , 1 ) \frac{X_2 + X_3}{\sqrt 2} \sim N(0, 1) 2 ​X2​+X3​​∼N(0,1)

同理，对于 Y 3 = b ( X 4 + X 5 + X 6 ) 2 Y_3 = b(X_4 + X_5 + X_6)^2 Y3​=b(X4​+X5​+X6​)2，它的样本集合 ( X 4 , X 5 , X 6 ) (X_4, X_5, X_6) (X4​,X5​,X6​) 的期望为0，方差为3，其标准正态分布为 X 4 + X 5 + X 6 3 \frac{X_4 + X_5 + X_6}{\sqrt 3} 3 ​X4​+X5​+X6​​

再从卡方分布的基本概念出发，拼凑出它应该为

X 2 = X 1 2 + ( X 2 + X 3 2 ) 2 + ( X 4 + X 5 + X 6 3 ) 2 = X 1 2 + ( X 2 + X 3 ) 2 2 + ( X 4 + X 5 + X 6 ) 2 3 X^2 = X_1^2 + \left (\frac{X_2 + X_3}{\sqrt 2} \right )^2 + \left ( \frac{X_4 + X_5 + X_6}{\sqrt 3} \right )^2 = X_1^2 + \frac{(X_2 + X_3)^2}{2} + \frac{(X_4 + X_5 + X_6)^2}{3} X2=X12​+(2 ​X2​+X3​​)2+(3 ​X4​+X5​+X6​​)2=X12​+2(X2​+X3​)2​+3(X4​+X5​+X6​)2​

所以， a = 1 2 a=\frac{1}{2} a=21​， b = 1 3 b = \frac{1}{3} b=31​

设 X ∼ N ( 0 , 1 ) X \sim N(0, 1) X∼N(0,1)， Y ∼ X 2 ( n ) Y \sim X^2(n) Y∼X2(n)，且 X, Y 相互独立，则称随机变量 t = X Y / n t = \frac{X}{\sqrt{Y / n}} t=Y/n ​X​ 服从自由度为 n n n 的 t t t 分布，记为 t ∼ t ( n ) t \sim t(n) t∼t(n)。 t ( n ) t(n) t(n) 分布的概率密度函数函数为：

h ( t ) = Γ [ ( n + 1 ) / 2 ] π n Γ ( n / 2 ) ( 1 + t 2 n ) − ( n + 1 ) / 2 , − ∞ < t < ∞ h(t) = \frac{\Gamma [(n+1) / 2]}{\sqrt{\pi n} \Gamma(n / 2)} (1 + \frac{t^2}{n})^{-(n+1) / 2}, -\infty < t < \infty h(t)=πn ​Γ(n/2)Γ[(n+1)/2]​(1+nt2​)−(n+1)/2,−∞