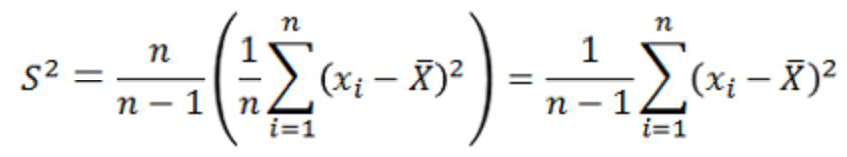如何理解《概率论与数理统计》中样本方差为何除以n

设样本均值为  ，样本方差为 S²，总体均值为  μ ，总体方差为 σ²，那么样本方差S²有如下公式： S²=，很多人可能都会有疑问，为什么要除以n-1，而不是n，但是翻阅资料，发现很多都是交代到，如果除以n，对样本方差的估计不是无偏估计，比总体方差要小，要想是无偏估计就要调小分母，所以除以n-1，那么问题来了，为什么不是除以n-2、n-3等等。所以在这里彻底总结一下，首先交代一下无偏估计。

以例子来说明，假如你想知道一所大学里学生的平均身高是多少，一个大学好几万人，全部统计有点不现实，但是你可以先随机挑选100个人，统计他   们的身高，然后计算出他们的平均值，记为。如果你只是把作为整体的身高平均值，误差肯定很大，因为你再随机挑选出100个人，身高平均值很可能就

跟刚才计算的不同，为了使得统计结果更加精确，你需要多抽取几次，然后分别计算出他们的平均值，分别记为：,...,然后在把这些平均 值，再做平均，记为：E() ，这样的结果肯定比只计算一次更加精确，随着重复抽取的次数增多，这个期望值会越来越接近总体均值，如果满足E()=μ，这就是一个无偏估计，其中统计的样本均值也是一个随机变量，就是的一个取值。无偏估计的意义是：在多次重复下，它 们的平均数接近所估计的参数真值。

介绍无偏估计的意义就是，我们计算的样本方差，希望它是总体方差的一个无偏估计，那么假如我们的样本方差是如下形式： S²=。

那么，我们根据无偏估计的定义可得：

由上式可以看出如果除以n，那么样本方差比总体方差的值偏小，那么该怎么修正，使得样本方差式总体方差的无偏估计呢？我们接着上式继续化简： 

到这里得到如下式子，看到了什么？该怎修正似乎有点眉目。

如果让我们假设的样本方差 乘以，即修正成如下形式，是不是可以得到样本方差是总体方差的无偏估计呢？

则：

 因此修正之后的样本方差的期望是总体方差  的一个无偏估计，这就是为什么分母为何要除以n-1。