| 概率论的学习整理1: 集合和事件,以及概率是什么? | 您所在的位置:网站首页 › 概率加法原则 › 概率论的学习整理1: 集合和事件,以及概率是什么? |
概率论的学习整理1: 集合和事件,以及概率是什么?
|
目录 为什么最近开始重新学习数学 1 集合 set 1.1 集合的基础概念 1.2 韦恩图,文氏图 1.3 韦恩图很有用 1.4 基本的集合关系 2 实验和事件 2.1 先贴下本地的笔记图 2.2 重要概念 2.2.1 事件 event 2.2.2 事件集 events 2.2.3 互斥事件: 交集为0 P(A∩B)=P(AB)=0 2.2.4 对立事件( 对立事件是互斥事件的一个特例) 2.2.5 独立事件 : 互不影响 P(AB) = P(A)P(B) 2.2.6 互斥事件和独立事件的关系 3 概率是什么? 对概率和事件的重新理解 3.1 概率是一种对世界的简化模型 3.2 比概率前置的重要事情,是弄清楚,我们要分析的“目标事件” 3.3 然后才是 抽象的概率学的各种理论 3.4 概率与面积,韦恩图(文氏图) 3.5 概率各种求法 4 关于概率,与先验后验等 5 对随机实验和事件的理解 5.1 随机实验 5.2 事件 6 《测度论》 7 如何理解 实验/目标事件 实际上是符合的,就是生活中的某一方面 7.1 单一维度的事件 7.2 复杂事件 8 辨析,独立事件 和 互斥事件 (写的太错了) 8.1 概念辨析 8.2 两个独立事件,是否互斥? 一定不互斥 8.3 两个互斥事件,是否独立? 互斥事件一定不独立 9 概率的加法和乘法原理 9.1 加法法则应用于并列关系的事件 9.2 乘法法则应用于不相干关系的事件 10 一些概率例题 10.1 相比于国外教材 10.2 例题1 10.3 例题2 10.4 例题3 10.4 例题4 为什么最近开始重新学习数学有用,有用,还是有用! 写在最前面的话 整理数学,是因为工作涉及到了,也是编程需要用到。所以我重新学了一段时间了,多年未学习了,几乎是从头开始了。关于写笔记,如果不自己写,感觉学了也会忘记,另外本地文档确实很没用,还是写网上文档把,CSDN的各种评价体系,我不care,我只是记个学习笔记。如果能尽量写的让初学者也能看懂,那就更好了。最近又重新学习了下数学,重新修改补充下这段内容关于我学习概率论的几个事情 我觉得学概率,肯定不能是为了做题,也不能靠做题。但是如果能把生活工作中遇到的问题都能从数学的角度去看,能去分析,并且解决,那真的太好了。如果问是问了什么?是为了解决问题,另外,希望孩子学概率论的时候能给孩子讲明白学习的小目标呢? 弄清楚原理理清楚知识体系,用脑图整理下。我觉得不能遇到概率提就想起各种公式,套公式,而是应该有个思路,能用树状图或者2维表展开,展开思考才行,后面的都应该是顺水推舟的事情。整理一下不同的解题思路,以后遇到类似问题提高效率 1 集合 set 1.1 集合的基础概念
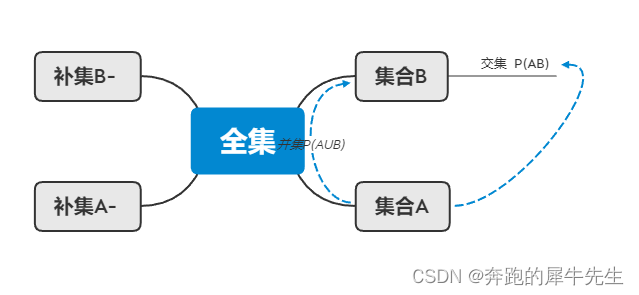
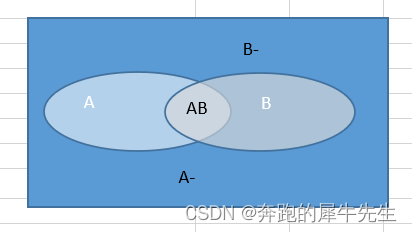
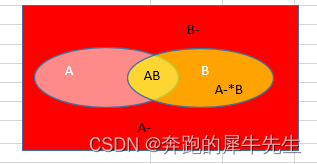
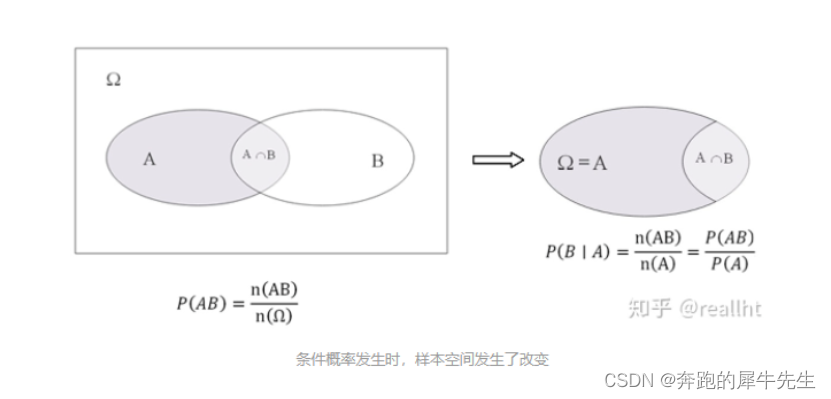
比如全概率公式 P(B)=P(A) *P(B|A) + P(A')*P(B|A') 很多人觉得并不好理解用下面这个图来理解全概率公式呢,很简单
以下内容仅为个人感觉和总结,先整理在这,之后需要再思考整理 3 概率是什么? 对概率和事件的重新理解 3.1 概率是一种对世界的简化模型 我现在觉得概率是看待世界的另外一种简化方式,只看发生还是不发生,发生概率大小 不看这个事件本身的影响大小。 世界很复杂,对世界的解读和抽象有很多种思路 有的是哲学,比如什么实体,精神这种抽象。 但是也有概率这个思考,这个角度,这个层面,把所有事务都抽象为1个最小单位---事件,就是只关心事务有没有发生,发生概率多少,而不关心事务内部 概率简化这个世界的角度,是否可以这么解释?可以认为事件就是一根棍子 I,这个棍子内有什么不关心了,棍子和其他棍子的联系只剩下一种,就是发生不发生,谁发生的概率大,这个有点像二进制抽象为01,是/否,或者周易那种抽象。其他信息通通丢弃掉不再关心。 3.2 比概率前置的重要事情,是弄清楚,我们要分析的“目标事件” (1)概率是对世界的一种简化 (2) 要理解概率,先搞清楚是对什么目标事件(不同事件的关系差别很大)的概率,其实目标事件,就是我们现实世界需要解决的问题。分析概率之前,先需要把这个事情本身分析清楚,逻辑条理清晰才行。 (3)然后再应用概率的一般理论 3.3 然后才是 抽象的概率学的各种理论 3.4 概率与面积,韦恩图(文氏图)韦恩图 样本空间=所有事件发生的集合(去重?) 样本空间 ={事件A1,事件A2,......} ={事件B1,事件B2,......} 不同维度的划分 概率 P(A1) = 面积比 = A占的面积 / 样本空间100%面积 正确的, p= 事件数/ 总事件数 错误的: p = p(A) / p()
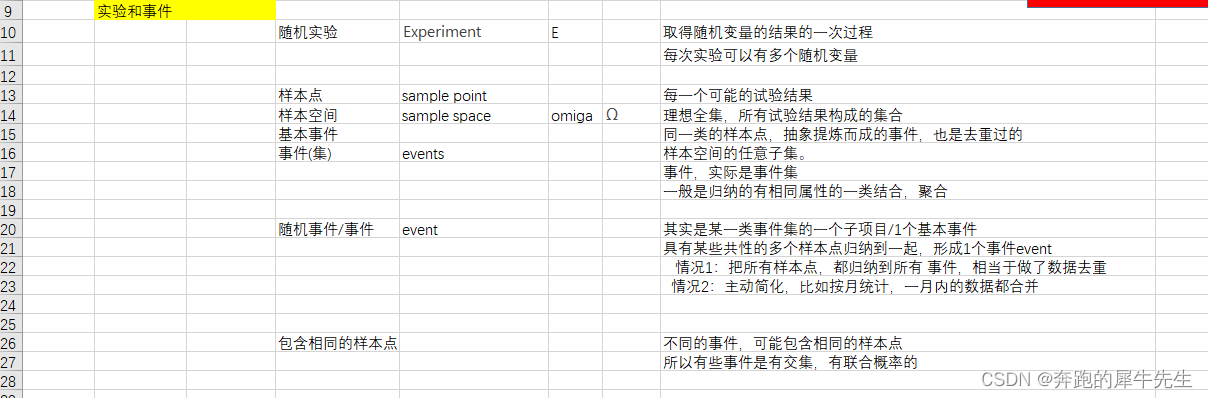
概率的最初来源,我觉得应该是来自于 统计,频次统计 频次不等于概率,但是可以用来估计概率?比如极大似然估计估计等? 1(后验的,统计的)频次 = 某事件发生次数/ 所有相关事件的发生次数总数,后验的统计的东西最重要的是总结规律,期待这个规则能指导以后的生活---其实就是预测,也就是 所谓的 经验指导未来。 2预测的理论模型,这个是需要的 (模型,理论分析)概率= 基础事件个数/总事件个数 3(先验的,用于预测)概率的= 事件发生的可能性/ 全部可能性100%=p ,有了先验的概率,则方便去演绎,推理等等,这么一套思考模型 4 信息进一步增加,(用新信息去修正老的概率)贝叶斯概率 条件概率公式: p(B|A) = p(AB) / p(A) bayes概率公式: p(B|A) = p(B)* p(A/ B) / p(A), 其中p(B)是老概率,而p(B|A)是修正后的概率。 5 对随机实验和事件的理解 5.1 随机实验 随机实验,只能是1次,或者多次如果是多个随机实验,那么这2个随机实验没关系实验不存在什么基础不基础,不再可以拆分,只有次数的差别很多一次实验,其实都是包含了多个维度的一次实验。比如有1个实验是,今天下雨/不下雨,另外1个实验是,今天下雨/不下雨 & 堵车/不堵车 5.2 事件 基本事件:就是针对某一个“目标事件”不可再分的最小事件? / 一些不可再分的结果事件(目标事件)=一些结果 = 一些结果组成的集合事件空间: (全部是相对的)全部基础事件组成的空间 / 全部结果 =全部结果组成的集合,不同情况下的全部空间是不一样的,某些概率对应的全部空间是全部,某系概率对应的全部空间只是其中一部分对分母的理解很重要,事件空间是相对的,比如 p(A)=p(AB)/p(B) ,样本空间是 A,B所在的全部空间Ω(=A+B+...)p(A|B)=p(AB)/p(B) ,样本空间就是B 6 《测度论》据说《测度论》更能说明和理解概率,需要以后学习 下面这个图是转载的,不是我画的
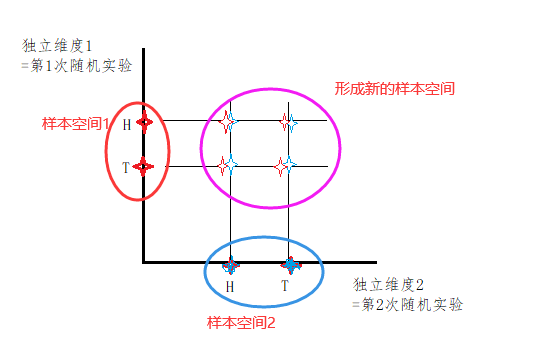
定义概率,需要定义为 p(Ω,F,p) 其中Ω是样本空间(但是需要是是定义再哪儿的样本空间,即使是等可能的样本空间也可能又不同的标准,并不一样),Ω里是独立的基础事件 F 是Ω的所有各种子集的 集合,而我们平时讨论某个变量的概率期望等只会取其中一个子集,并且子集的取法不同,最终计算的概率也会不同。 p 是对基本事件的目标组合 (即使是一些等概率模型,不同的样本空间定义和变量选择,最终概率会不一样) 举例子 贝朗特悖论里,三种不同的概率结论就是,虽然都是等可能,但是概率空间Ω的定义不同导致最终概率也不同。所以这里必须定义清楚,否则可能会出现如下问题这种 几种方法概率不同。 概率论的学习和整理--番外9:关于贝特朗悖论的学习(没搞懂)_贝特朗箱子悖论_奔跑的犀牛先生的博客-CSDN博客贝特朗悖论_贝特朗箱子悖论下雨和堵车,独立事件,不互斥(现有知识条件下)可能同时发生 下雨和世界大战,独立事件, 下雨和摆摊,非独立事件,但是互斥? 复杂事件往往多有多个事件构成的,这个往往跟我们人类提出的问题相关 目标问题是复杂的 = = 样本空间复杂 比如 下雨,堵车,这本身可以说是2个独立事件如果我们想要知道 p(明天下雨 & 堵车) =1/4可以做成下图的4方格(交叉图)来理解下雨 50% 不下雨 50% 堵车 50% 下雨&堵车 不下雨&堵车 不堵车 50% 下雨&不堵车 不下雨&不堵车 用图可以这么表示,这个过程
互斥的例子 一个指标内,比如性别里的男女是互斥的,比如年龄里的19和20,21等就都是互斥的 不可再分(很难再分)的划分维度下的属性下的不同分类 独立的例子 而性别,年龄,国家。这些不同维度里拿出的变量,就是独立的变量 复合维度划分 1 是中国男孩的概率是多少?2 是30岁女性的概率多少等等所以,从上面的例子看 1 互斥事件,看起来一定是一个不可再分(很难再分)的划分维度下的属性下的不同分类,比如性别,年龄等2独立事件,性别 & 年龄 & 国籍,考虑目标事件时需要结合考虑,计算时可以拆分考虑 比如要考虑 30岁女性,那么就需要结合起来考虑,但是计算时可以拆分 但是,显示结果时需要,结合考虑 p(30岁 & 女性)= p(30岁) * p(女性)8.2 两个独立事件,是否互斥? 一定不互斥 如果2个事件独立,也就是存在一般意义的2个维度(属性维度)的事件,那么是否互斥,是不确定的比如,1个30岁人类,可能 是男性,或者是女性 抽象30岁人类这个属性,本身不会和 性别 互斥,他们是独立的但是任一个 具有 30岁属性的人类这个实验结果,可能是男性,也可能是女性 相互独立事件同时发生的概率P(AB) = P(A) *P(B) P(B|A)=P(B) 也就是独立事件的交集可能=0,也可能不=0 8.3 两个互斥事件,是否独立? 互斥事件一定不独立 互斥的2个事件,一般就是指同一个(最小不可再分)属性维度下的2个事件互斥意味着,这2种事件结果不能同时发生,2个事件的交集=0互斥事件,一定不独立因为互斥事件,1个事件(结果)发生了,另外一个事件(结果)一定不发生,这2个事件是互相影响的,并且是不能同时存在的这种影响。 互斥的事件互相没有交集,计算概率时一般是相加,加法原则 9 概率的加法和乘法原理 9.1 加法法则应用于并列关系的事件概率加法,一般是用在独立事件概率 概率加法,对应加法原理 比如完成一件事有很多方法,每个方法都可以独立完成,完成这件事的概率 = 每种方法概率 累加 9.2 乘法法则应用于不相干关系的事件 概率乘法,一般是用在条件概率概率乘法,对应乘法原理比如完成一件事有很多步骤,每个方步骤都有一定概率,完成这件事的概率 = 每个步骤概率的累乘 10 一些概率例题 10.1 相比于国外教材千万别相信什么同济教材,浙大教材,懂得都懂 10.2 例题1红黄蓝三种颜色的小球各10个,每种颜色小球上分别从0到9标上数字。随机抽球。抽到红色偶数数字的球的概率是多少? 用加法原理,一共五个球,抽到每个的概率1/30,五个1/30相加得1/6用乘法原理,抽到红色球概率10/30,其中抽到偶数数字概率5/10,相乘得1/6 10.3 例题2一共有五张卡a、b、c、d、e,抽一次,抽中卡a或b或c或d就算中奖,那么中奖的概率应当是0.8,抽中a的概率为0.2。 事件算法: 4/5加法原则:中奖概率1/5+1/5+1/5+1/5=4/5乘法原则:就一个步骤,第一个步骤中奖概率=4/5 10.4 例题3https://www.zhihu.com/question/381514613/answer/1270736936
https://zhidao.baidu.com/question/332991559.html?qbl=relate_question_2 现在4张奖券,其中只有一张有奖,4位同学不放回地抽取,若已知第一位同学抽后未中奖,则第三位同学也抽不到中奖奖券的概率答案2/3 P=1/4 第1人已经抽奖,且没中,样本空间等都变化了 用条件概率怎么表示??? p=1/3 整体看 第2人抽奖,1/3中奖, 2/3不中奖 第3人抽奖,1/3中奖, 2/3不中奖 第4人抽奖,1/3中奖, 2/3不中奖 |
【本文地址】