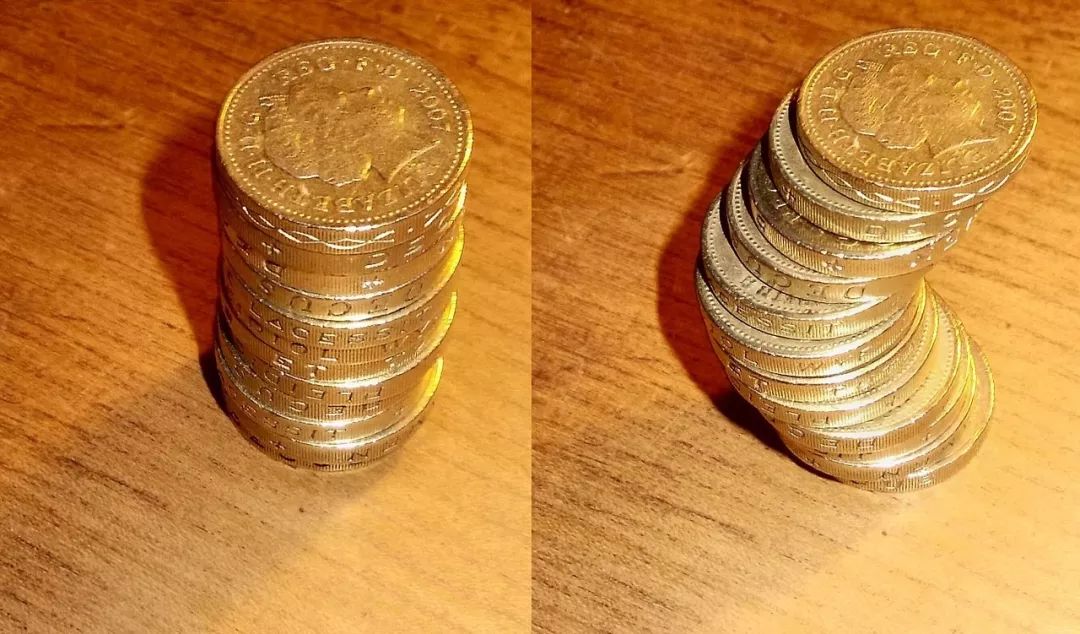写给5年级的学生：球公式是如何推导出来的？

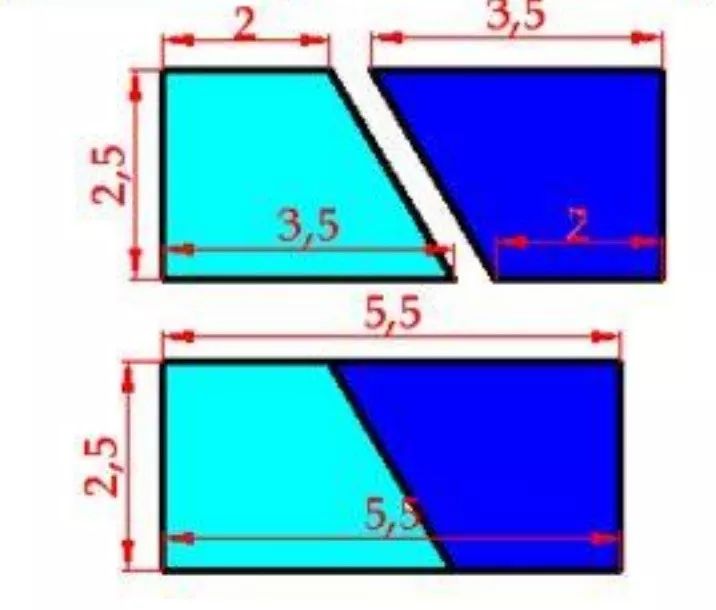
把两个三角形或者两个梯形一正一反拼起来，得到了长方形。由此得到三角形的面积是长方形的一半， 也就是(底*高)/2，而梯形的面积是 (上底 +下底)* 高/2。甚至可以说，三角形是梯形面积公式的特例，三角形是上底 =0的梯形，长方形则是上下底相同的梯形。所以只需要一个梯形公式就够了，它概括了全部三种情形。

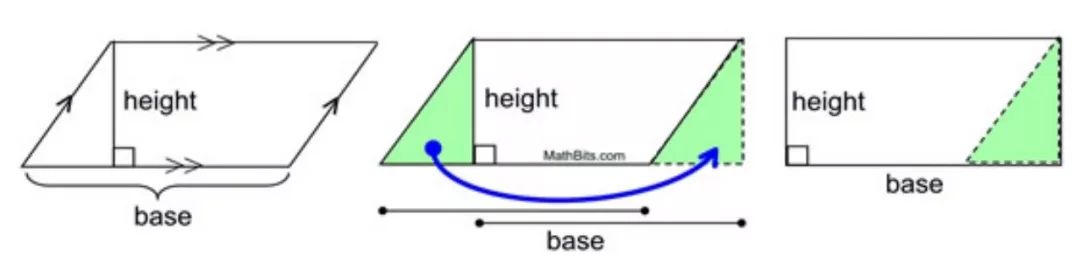
图：两个直角梯形拼成长方形，摘自easycoursesportal.com

大数学家高斯小时候算1+2+3+...+100=5050的故事，大家恐怕是耳熟能详了。高斯使用的等差数列求和公式，总和= (首项+末项)* 项数/2，本质上和梯形面积公式是一回事：首项、末项分别是上底和下底，项数是高。这个例子看出数学是广泛联系的整体，求数列和、求面积体积、求积分，都是一个东西，只是符号不同罢了。

斜三角形面积和祖暅原理

好学的孩子可能会马上指出，上面的做法计算三角形和梯形的面积，只适用于直角三角形和直角梯形。为什么对一般的“斜三角形、斜梯形”也成立？

简单的解释是斜三角形，一正一反会拼成等底等高的平行四边形。而平行四边形可以不断切掉斜角补到另一侧（有时可能要做多次），变成一个等底等高的长方形。所以平行四边形的面积也是底 * 高，上面三角形和梯形公式仍然成立。

图：平行四边形面积等于长方形面积，摘自 mathbits.com

然而有更好的解释：任意两个等高的图形，如果对应高度上的平行截线长度都相同，则它们的面积相同。这是个很强大的原理，并不限于三角形和梯形。而且在三维空间上也成立：任意两个等高的物体，如果对应高度上的平行截面积都相同，则它们的体积相同。

图：根据祖暅原理，左右两个图形面积相等，摘自 mathbits.com

这就是有名的祖暅原理，由南北朝时期的数学家祖暅之提出。祖暅之是祖冲之的儿子，他们父子都很了不起，是中国古代数学的骄傲。西方数学文献中，这个原理被归在十七世纪意大利数学家卡瓦列里（Bonaventura Francesco Cavalieri）的名下。

祖暅原理不难理解：想象每个高度上，都被一个很细的小条覆盖住，小条的长度是这个高度上的截线长度，厚度是个很小的d 。所有小条的面积加起来就是图形的面积 —— 有些小误差，但是当 d -> 0 时误差就缩小到0，得到精确面积。既然这两个图形在每个高度上的截线长度都相同，对应的小条的面积也相同，所以总面积自然也一样。上述推理应用到三维空间也成立，只要把“截线长度”换成“截面面积”就好了。

维基百科的条目上给了个有趣的图示：想象桌上放一摞硬币，堆成的柱体的体积就是硬币的总体积（左图）。把硬币随意水平移动，得到了另一个柱子（右图）。新柱子的每个截面面积和原来的柱子的对应截面面积一样，体积也没变，因为还是那堆硬币的总体积。这个例子展示了祖暅原理的原因。

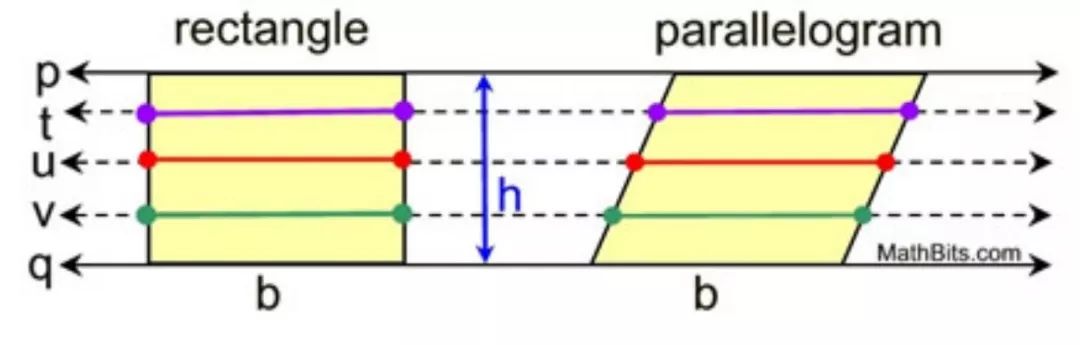
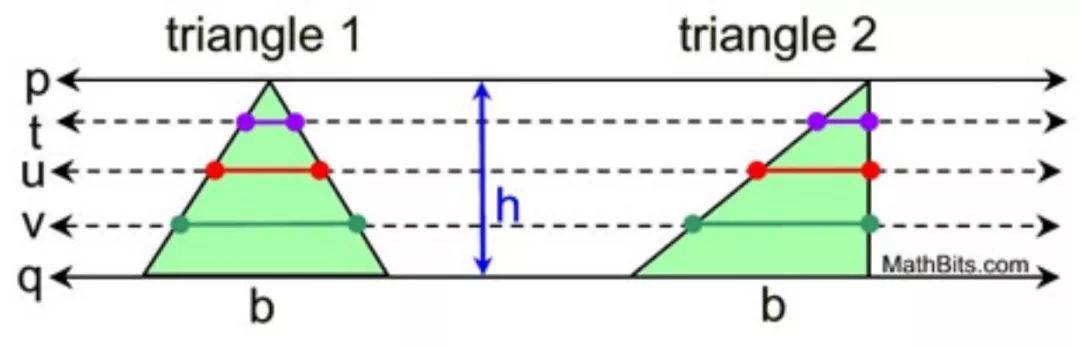
图：摘自Wikipedia

祖暅原理告诉我们，平行四边形面积和等底等高的长方形面积相等，因为每个高度的截线长度都相等。同理，等底等高的三角形（或梯形）的面积也是相等的，因为根据相似性，它们也满足祖暅原理的条件。

图：根据平行线分线段成比例定理，左右两个三角形对应高度的截线相等。根据祖暅原理，它们面积相等。摘自 mathbits.com

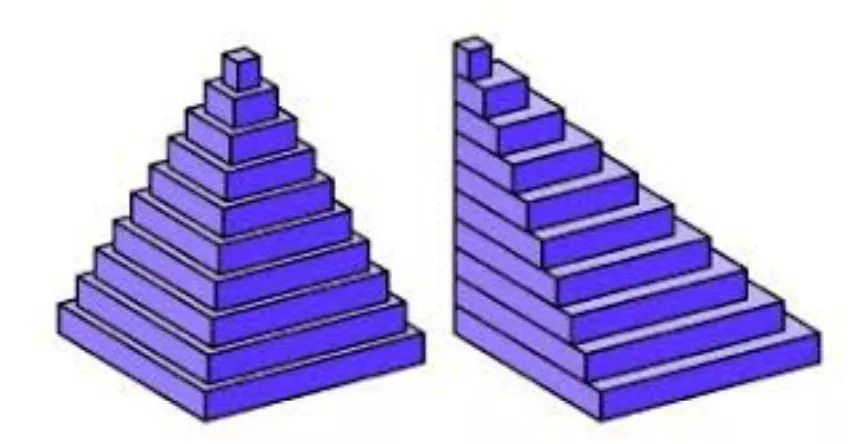
图：三维空间的祖暅原理：左右两个物体体积相同。摘自 brown.edu

长方体、棱锥、圆柱、圆锥、锥台体积

现在说体积。我们熟知棱柱或圆柱体积 =底面积 * 高，而棱锥和圆锥的体积，是同底同高的棱柱或圆柱体体积的1/3 ，也就是 底面积 * 高/3。为什么呢？

利用上面数方块的办法，知道长方体的体积 = 底面积 * 高。一个正方体，可以恰好切成三个全等的“直角金字塔”，每个金字塔的底面是正方体的一面，高是正方体的边长。

图：摘自 math.brown.edu

所以底面为正方形、高为正方形边长的棱锥的体积为等底等高棱柱的1/3 。根据祖暅原理和相似性，很容易把这个结论推广到一般的棱锥和圆锥。

计算球体体积

心急的观众可能要等不及了：绕了这么半天，怎么还没说到球体？好消息是：现在就说 — 因为准备工作已经做足了。

表面积

说到这里，已经回答了最初的问题。然而还有两件事情值得一说。其一，不仅球表面积可以看成是球的“底面”，用棱锥公式推导球体积；平面上的圆也可以看成是很多等高的小三角形拼成，用三角形面积公式= 底* 高/2来算。这里高是圆半径，三角形的底的和是圆周长。所以圆面积 = 圆周长 * 高/2。

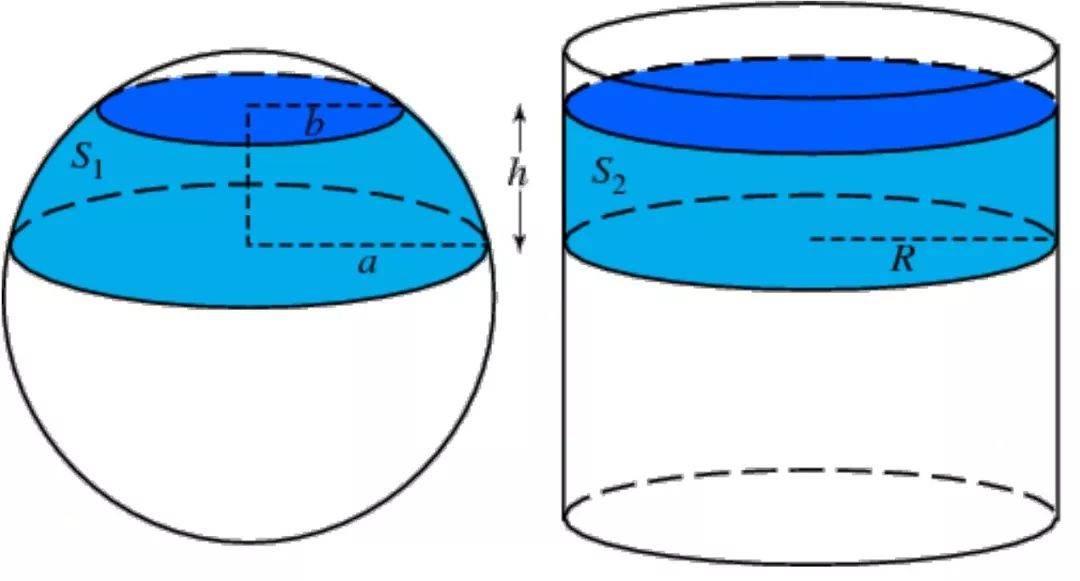
这个规律甚至在更高的维度也成立， N维空间的球体积有如下的漂亮公式： 球体积=球表面积 * 半径/N。这里系数1/N 来自N 维空间中的“棱锥”（学名是单纯形）和对应的长方体（超矩形）的体积关系。看，原来球就是个底面自我封闭的棱锥，如此而已。

直接计算球表面积

另一件值得提及的事情，是有没有可能不通过体积，直接计算球表面积？事实上，球的表面积和一个半径为R，高度为2R的圆柱侧面积是一样的。下图左侧的球和右侧的圆柱半径相等，高度也相等，也就是球可以刚好装进这个圆柱里卡住。这个圆柱的侧面积（不包含上下底），很容易计算：

恰好是我们知道的球表面积。

图：摘自 wolfram mathworld

其实球的表面积和圆柱侧面积是“一一对应”的，用任何一对平行平面切出来的球带面积（左侧浅蓝区域）和对应的圆柱侧面积（右侧浅蓝区域）都是相等的。这件事情最早被阿基米德写在著作《论球与圆柱》中，被后人称作“Archimedes’ Hat-Box Theorem”。

总结

球体的几何性质是个迷人的领域，这里尝试用初等的数学和几何直观，解释阿基米德和祖氏父子这些先驱们所发现的事情。是否达到了“让小学五年级的孩子理解”无从判断，但是总算躲开了微积分等高深的数学语言。个人感觉把数学原理用简单语言解释，既是很大的挑战，也是个“返璞归真”的机会，来重新看到隐藏在抽象符号后面那些直观的道理。

请问读者：这个推理错误的原因是什么？

图：算球表面积的错误方法，转自百度文库

本文作者waikok，清华计算机本科及博士，谷歌码农，娃爸，喜读书，好古文，爱编程，业余时间琢磨数学。返回搜狐，查看更多