树状数组学习笔记

树状数组，也称作“二叉索引树”（Binary Indexed Tree）或 Fenwick 树。 它可以高效地实现如下两个操作：1、数组前缀和的查询；2、单点更新。下面具体解释这两个操作。

首先看下面这个例子，了解什么是数组的前缀和查询。

例1：已知数组 $[10, 15, 17, 19, 20, 14, 12] $。

1、求索引 $0$ 至索引 $4$ 的所有元素的和； 2、求索引 $0$ 至索引 $5$ 的所有元素的和； 3、求索引 $0$ 至索引 $7$ 的所有元素的和。

“前缀和”定义了一个数组从“头”开始的区间，计算的是这个从索引位置是 $ 0$ 开始的区间中的所有元素的“和”。

注意：我们的基本问题是解决从索引位置是 $0$ 开始的所有元素的和，而其它不是从 $0$ 开始的数组的区间和可以转化成前面的这个问题。这一点可以看后面的例 4 。

例 2：已知数组 $[10, 15, 17, 19, 20, 14, 12]$ 。

1、将索引为 $4$ 的元素增加 $2$； 2、将索引为 $6$ 的元素减少 $3$。

“单点更新”定义了将数组指定索引的元素值变更为另一个值，给出的参数是一个改变的数值，即“更新以后的值-原来的值”。注意，单点更新的操作，我们描述的是“相对于之前的值发生的变化”，而不是“变成了什么”。

如果我们不使用任何数据结构，仅依靠定义，“数组前缀和的查询 ” 的时间复杂度是 $O(n)$，“单点更新” 的时间复杂度是 $O(1)$。 我们觉得“数组前缀和的查询 ” 的时间复杂度较大，要扫描这个区间的一大部分元素，才能得到这个区间的和。于是一个常见的做法是，我们可以首先计算出一个“前缀和数组”，这个数组的每个元素的值对应的正是原来数组的前缀和。

例3：已知数组 nums = [1, 2, 3, 4, 5, 6, 7]，求前缀和数组 cumsum。

分析：根据前缀和的定义，容易计算前缀和数组是 cumsum = [1, 3, 6, 10, 15, 21, 28]。

有了前缀和数组每次查询前缀和时间复杂度就变成了 $O(1)$。前缀和数组得到以后，就可以以 $O(1)$ 的时间复杂度解决“区间和”问题。

例4：已知数组 nums = [1, 2, 3, 4, 5, 6, 7] ，求区间 [3, 7] 的和，特别说明：该例中数组的索引从 $1$ 开始计算。

说明：注意到这个例子有一个特别说明“该例中数组的索引从 $1$ 开始计算”，大家先不要纠结为什么。因为后续我们对树状数组的定义都选择从索引 $1$ 开始，这和堆的一般实现思想类似，索引 $0$ 我们不放元素。这个例子只是为了说明“已知前缀和可以用 $O(1)$ 的时间复杂度得到区间和”。

分析：由于“前缀和(7)” = nums[1] + nums[2] + nums[3] + nums[4] + nums[5] + nums[6] + nums[7] ； “前缀和(2)” = nums[1] + nums[2]； 而“区间 [3, 7] 的和”= nums[3] + nums[4] + nums[5] + nums[6] + nums[7]； 所以，“区间 [3, 7] 的和” = “前缀和(7)” - “前缀和(2)” 。

从这个例子中，我们可以看出：前缀和数组知道了，区间和也可以很快地求出来。

那如果我要执行“单点更新”，就得更新这个前缀和数组，又得计算一次前缀和，时间复杂度为 $O(n)$。 那如果我在一次业务场景中“前缀和”和“单点更新”的次数都很多，前缀和数组就不高效了。而 Fenwick 树就是“高效的”实现“前缀和”和“单点更新”这两个操作的数据结构。

我们首先先看看树状数组长什么样，有一个直观的认识。

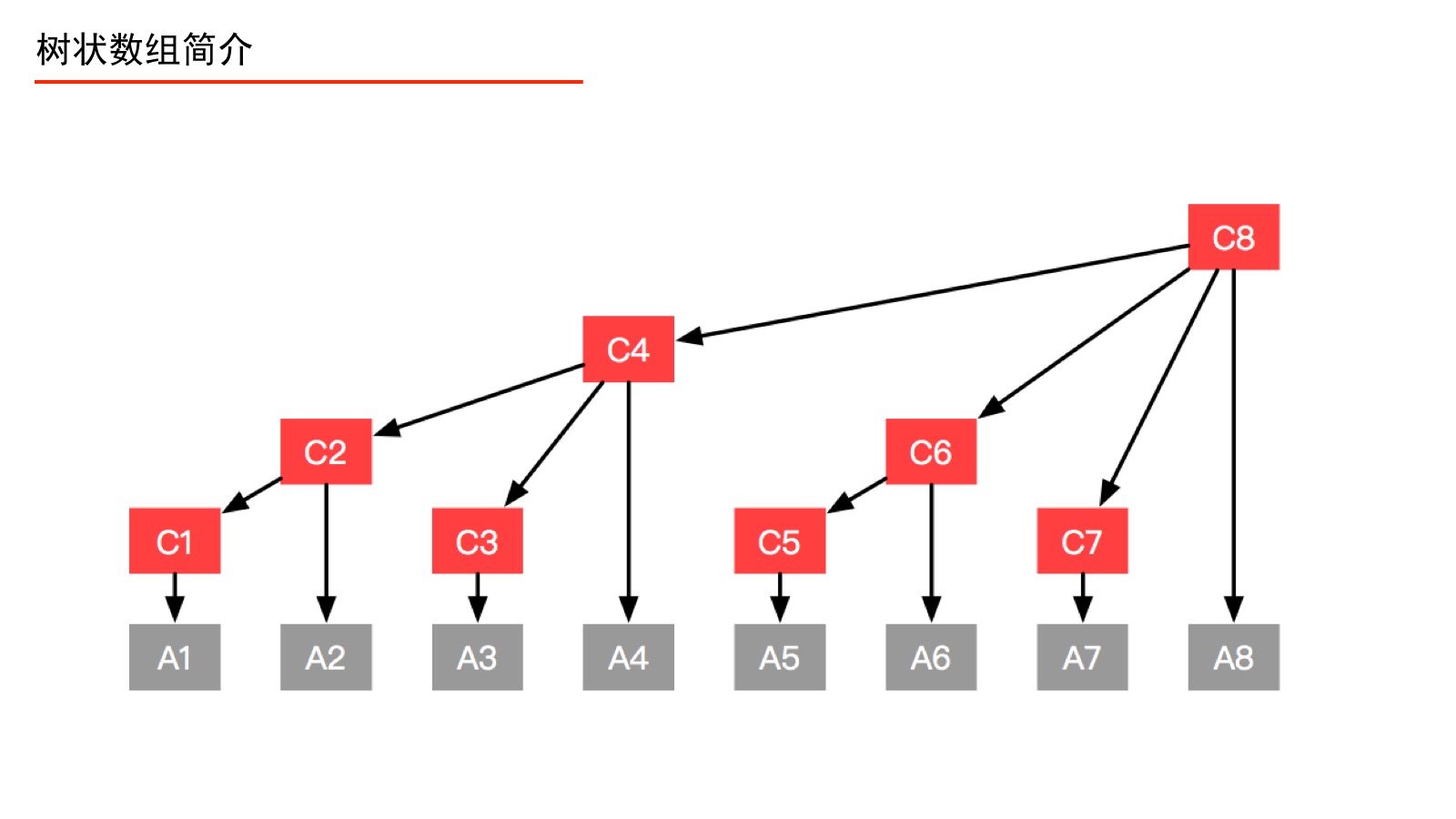
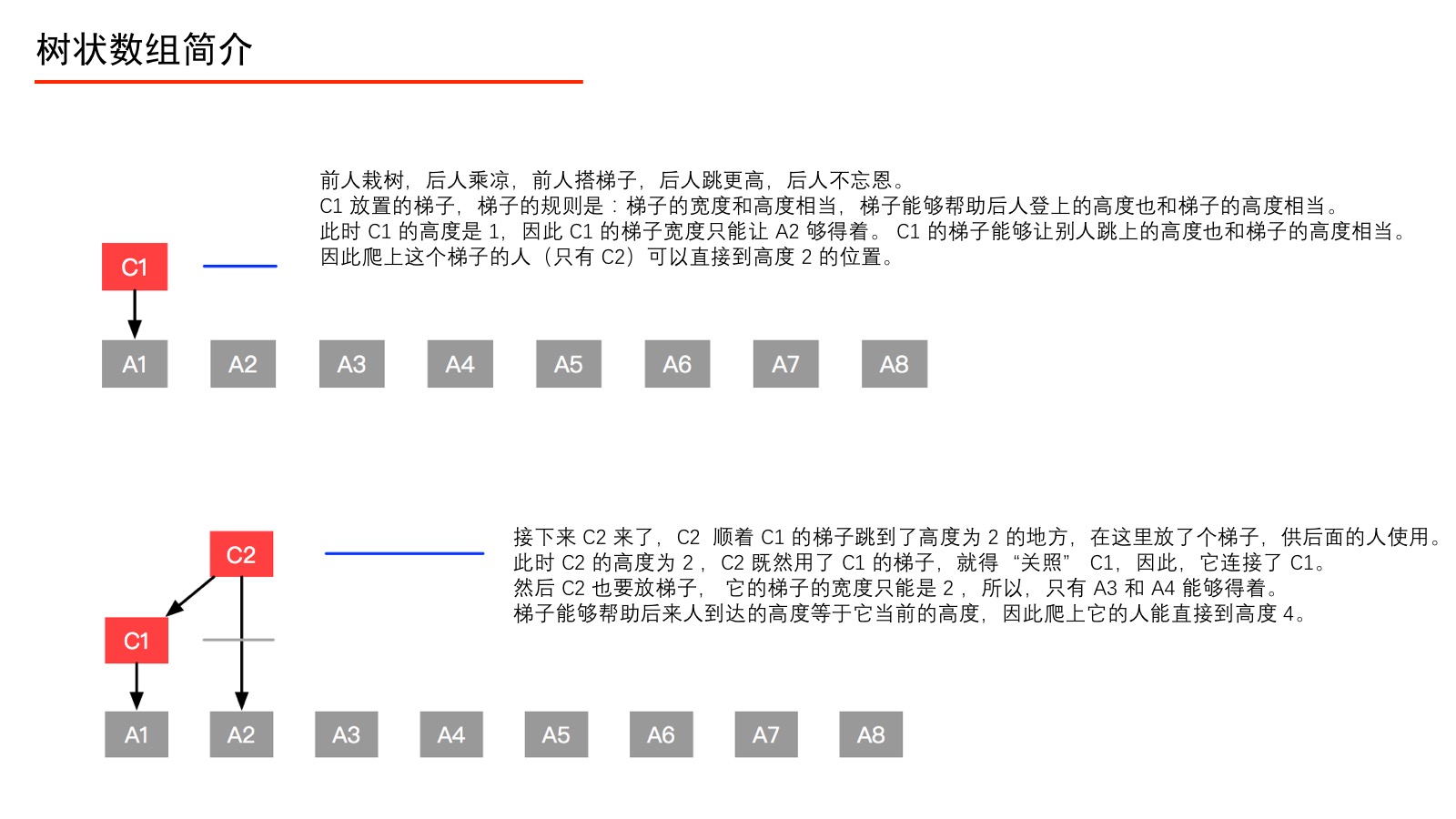
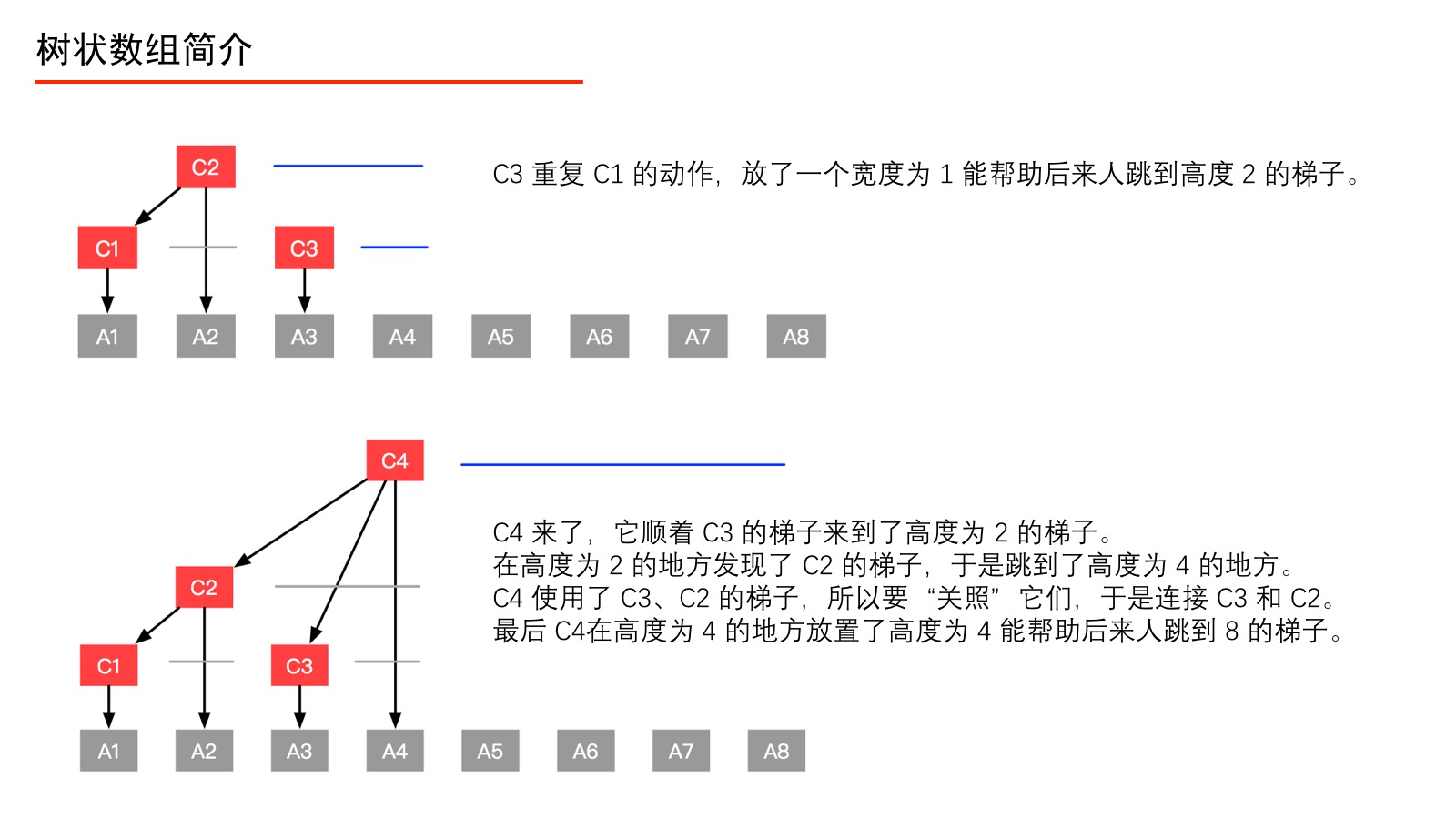
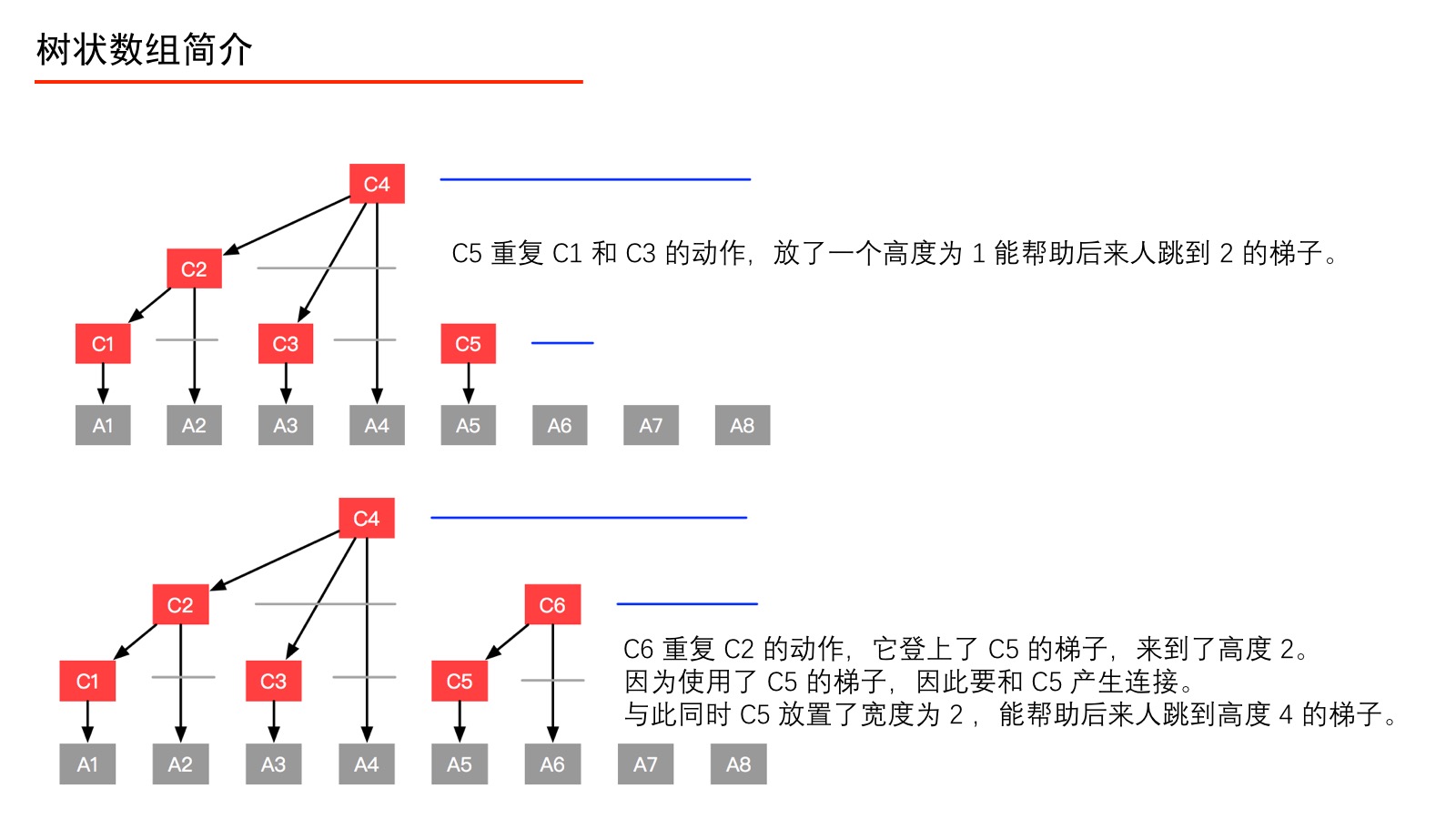
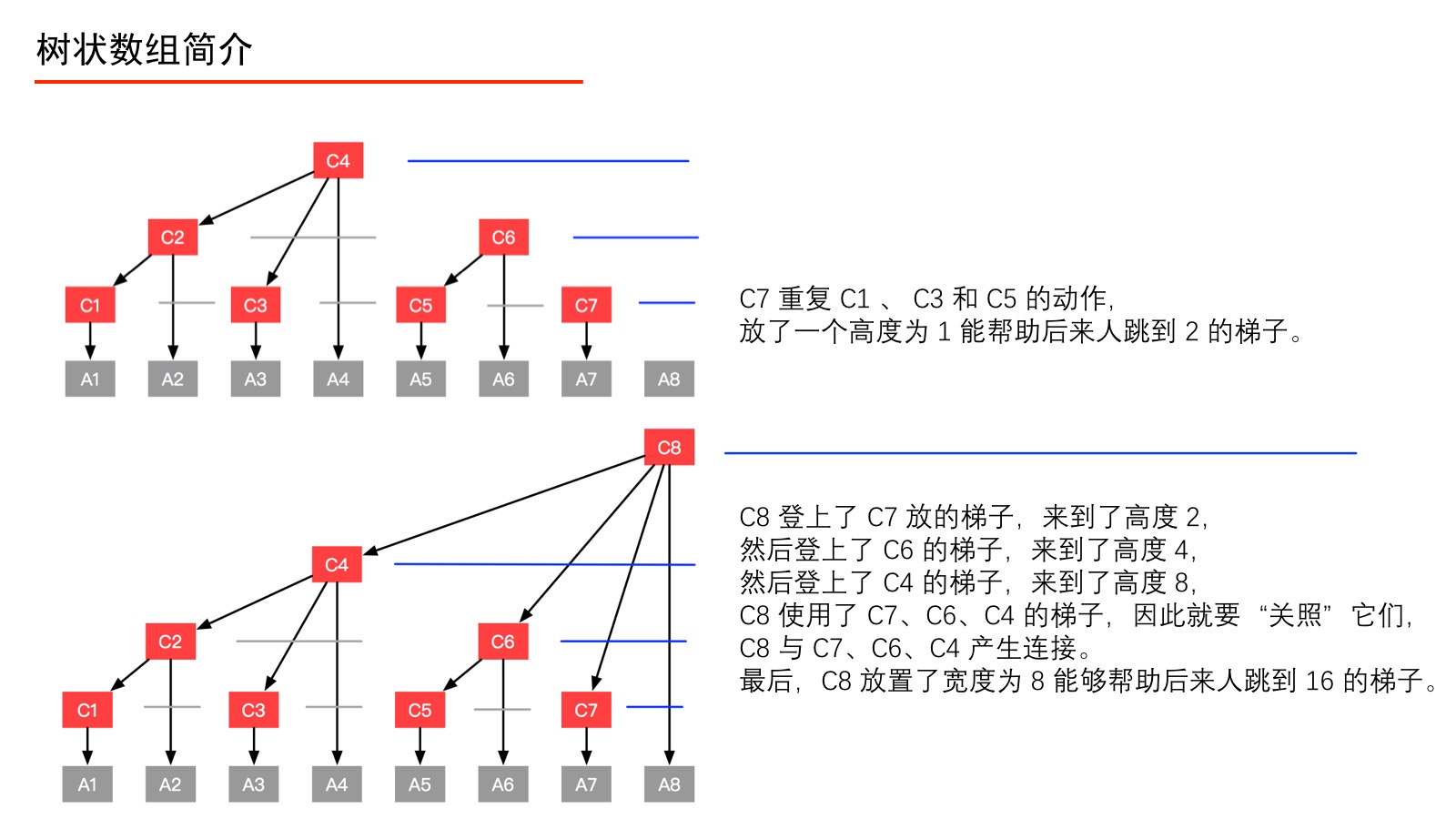
例5：我们以一个有 $8$ 个元素的数组 A 为例（如上图），在数组 A 之上建立一个数组 C，使得数组 C 的形成如上的一个多叉树形状，数组 C 就是一个树状数组。此时我们有以下疑问：

分析：不。学习过堆、线段树的朋友一定知道，使用数组就能方便地索引左右孩子结点、双亲结点（因为规律特别容易找到），这样的树就不必创建成结点、指针那样的动态树形结构。

补充说明：这一段看不明白没有关系，耐着性子往后看。我们构建好数组 C 以后，就完全可以抛弃数组 A 了。

在这个小数组中，可能我们无法体会到 Fenwick 树的威力，请大家稍安勿躁，学习到后面，你就知道为什么 Fenwick 树对于“前缀和查询”和“单点更新”都非常频繁的业务来说是高效的。

首先我们强调一下，树状数组的下标从 $1$ 开始计数，这一点我们看到后面就会很清晰了。我们先了解如下的定义，请大家一定先记住这些记号所代表的含义：

1、数组 C 是一个对原始数组 A 的预处理数组。

2、我们还要熟悉几个记号。为了方便说明，避免后面行文啰嗦，我们将固定使用记号 $i$ 、$j$ 、 $k$，它们的定义如下： 记号 $i$ ：表示预处理数组 $C$ 的索引（十进制表示）。 记号 $j$ ：表示原始数组 $A$ 的索引（十进制表示）。 我们通过以下的图，来看看 C1、C2、C3、C4、C5、C6、C7、C8 分别是如何定义的。

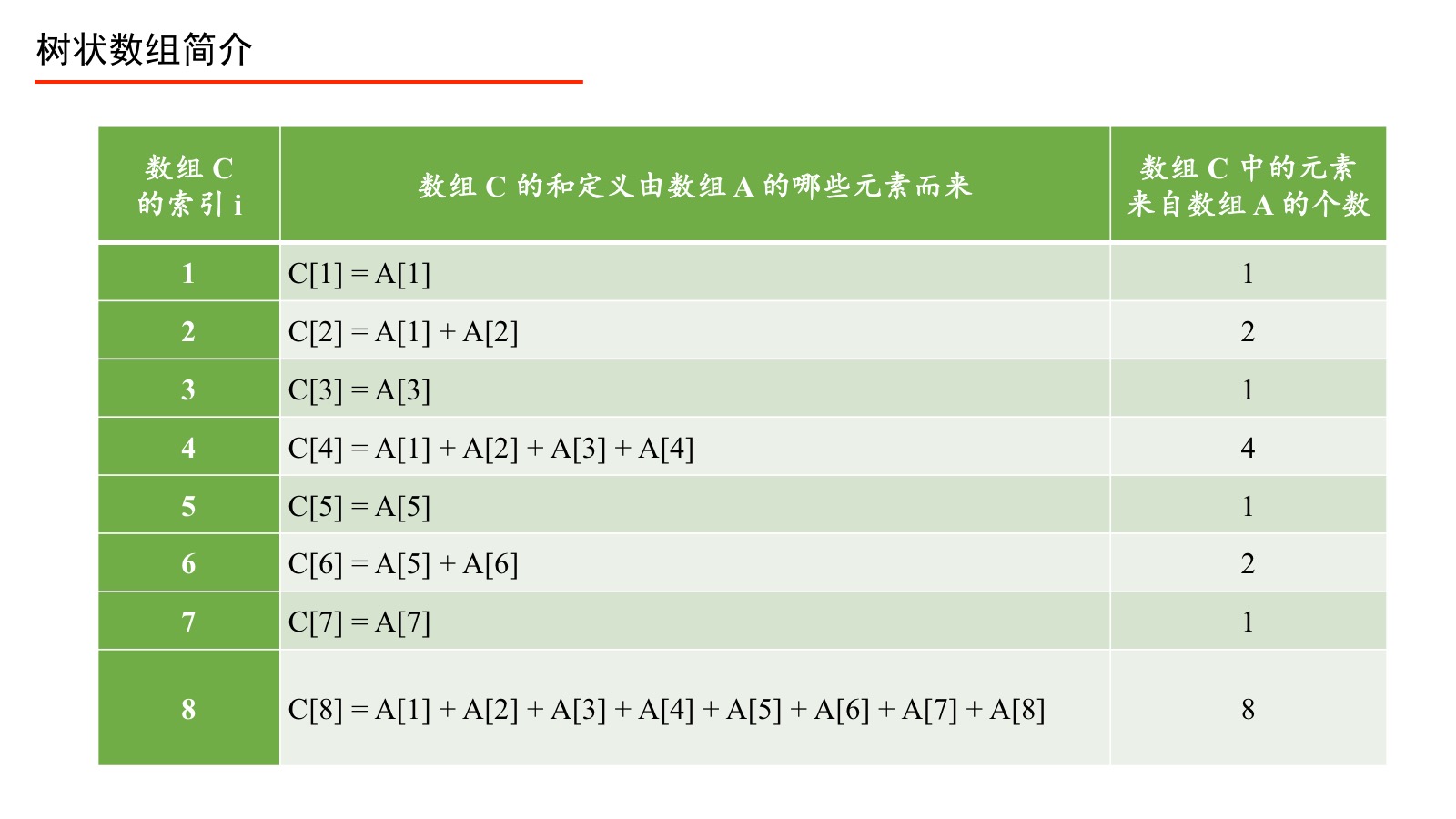
上面的过程我们用如下的表来表示。

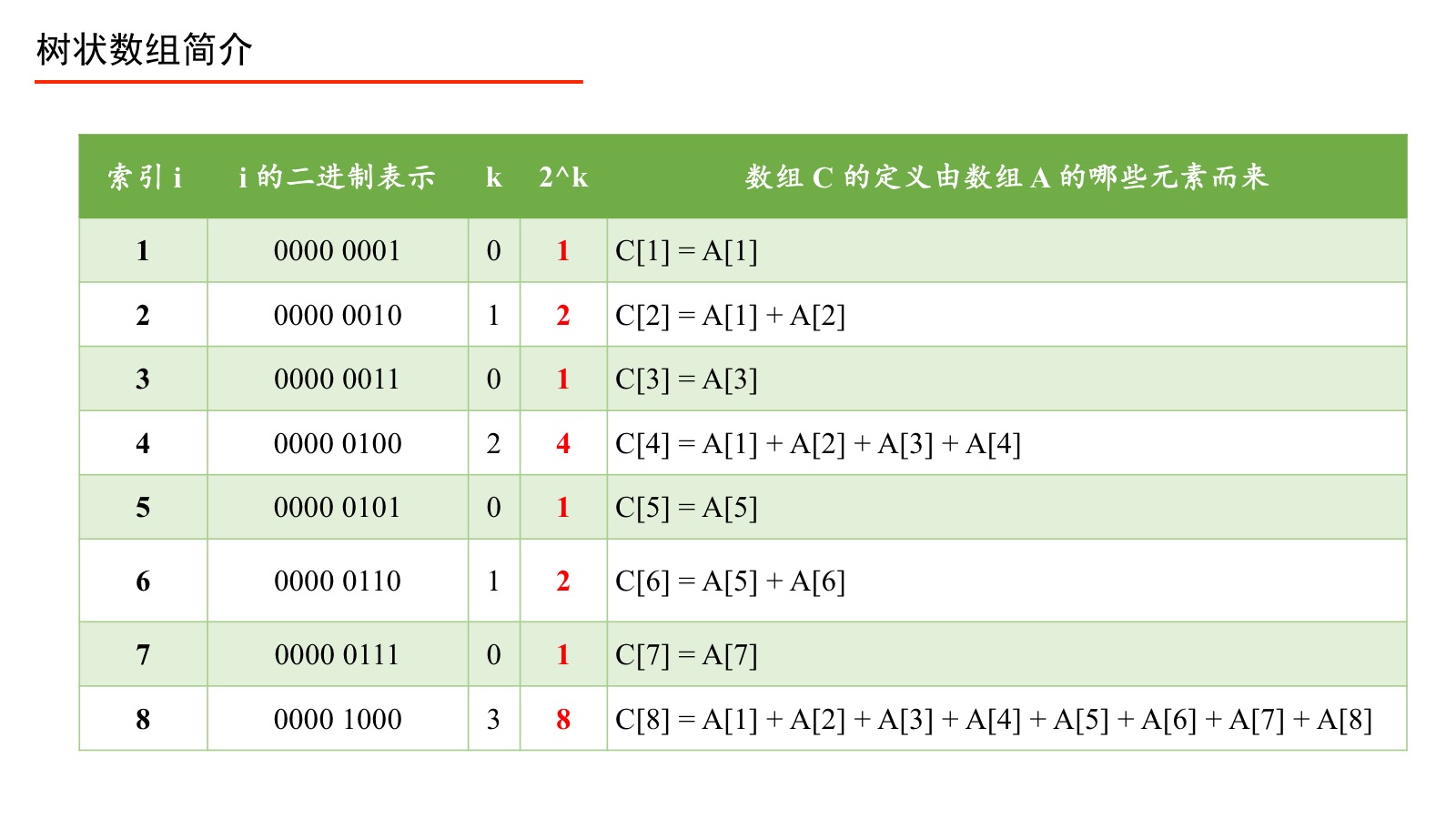
伟大的计算机科学家注意到上表中标注了“数组 $C$ 中的元素来自数组 $A$ 的元素个数”，它们的规律如下：将数组 $C$ 的索引 $i$ 表示成二进制，从右向左数，遇到 $1$ 则停止，数出 $0$ 的个数记为 $k$，则计算 $2^k$ 就是“数组 $C$ 中的元素来自数组 $A$ 的个数”，并且可以具体得到来自数组 $A$ 的表示，即从当前索引 $i$ 开始，从右向前数出 $2^k$ 个数组 $A$ 中的元素的和，即组成了 $C[i]$。下面具体说明。

记号 $k$ ：将 $i$ 的二进制表示从右向左数出的 $0$ 的个数，遇到 $1$ 则停止，记为 $k$。 我们只对数组 $C$ 的索引 $i$ 进行这个计算，数组 $A$ 的索引 $j$ 不进行相应的计算。理解 $k$ 是如何得到的是关键，请务必重视。下面我们通过两个例子进行说明。

例5：当 $i = 5$ 时，计算 $k$。

分析：因为 $5$ 的二进制表示是 $0000\;0101$，从右边向左边数，第 $1$ 个是 $1$ ，因此 $0$ 的个数是 $0$，此时 $k=0$ 。

例6：当 $i = 8$ 时，计算 $k$。

分析：因为 $8$ 的二进制表示是 $0000\;1000$，从右边向左边数遇到 $1$ 之前，遇到了 $3$ 个 $0$，此时 $k$ = 3。

计算出 $k$ 以后，$2^k​$ 立马得到，为此我们可以画出如下表格：

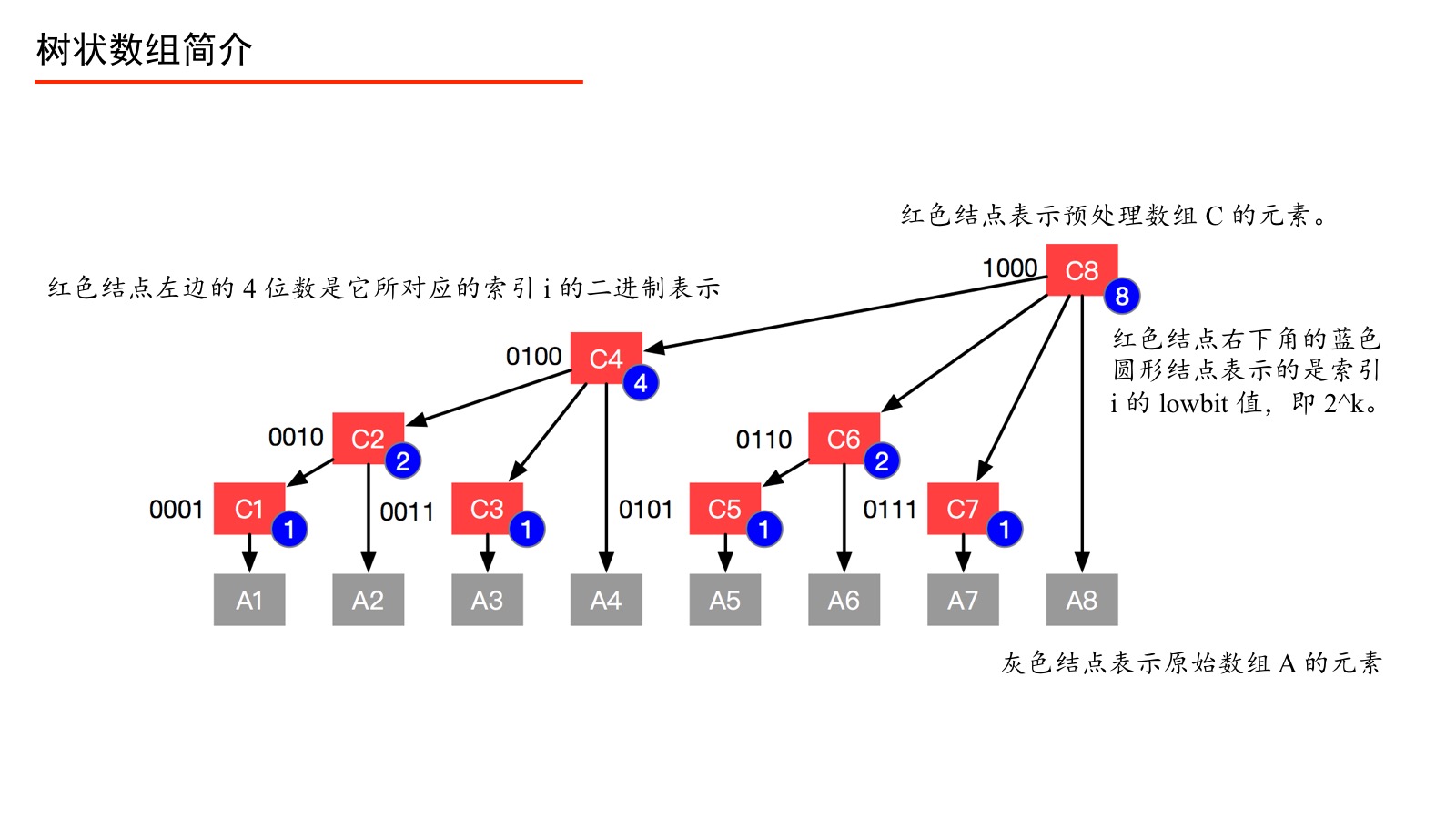
我们看到 $2^k$ 是我们最终想要的。下面我们介绍一种很酷的操作，叫做 lowbit ，它可以高效地计算 $2^k$，即我们要证明：

$$ {\rm lowbit}(i) = 2^k $$

其中 $k$ 是将 $i$ 表示成二进制以后，从右向左数，遇到 $1$ 则停止时，数出的 $0$ 的个数。

对，就是这么简单。理解这行伪代码需要一些二进制和位运算的知识作为铺垫。

首先，我们知道负数的二进制表示为：相应正数的二进制表示的反码 + 1。

例7：计算 $-6$ 的二进制表示。

分析：$6$ 的二进制表示为 $0000\;0110$，先表示成反码，即“ $0$ 变 $1$，$1$ 变 $0$”，得 $1111\;1001$，再加 $1$，得 $1111\;1010$。

例8：当 i = 6 时，计算 ${\rm lowbit}(i)​$ 。

分析：由例 7 及“与”运算的定义，把它们按照数位对齐上下写好：

说明：上下同时为 $1​$ 才写 $1​$，否则写 $0​$，最后得到 0000 0010，这个二进制数表示成十进制数就是 $2​$。建议大家多在稿纸上写几个具体的例子来计算 ${\rm lowbit}​$，进而理解为什么 ${\rm lowbit}(i)=2^k​$。

下面我给出一个我的直观解释：如果我们直接将一个整数“按位取反”，再与原来的数做“与”运算，一定得到 $0$。巧就巧在，负数的二进制表示上，除了要求对“按位取反”以外，还要“加” $1$，在“加 ” $1$ 的过程中产生的进位数即是“将 $i$ 表示成二进制以后，从右向左数，遇到 $1$ 停止时数出 $0$ 的个数”。

那么我们知道了 ${\rm lowbit}$ 以后，又有什么用呢？由于位运算是十分高效的，它能帮助我们在树状数组中高效计算“从子结点索引到父结点”（即对应“单点更新”操作），高效计算“前缀和由预处理数组的那些元素表示”（即对应“前缀和查询操作”）。

例9：修改 $A[3]​$， 分析对数组 $C​$ 产生的变化。

从图中我们可以看出 $A[3]$ 的父结点以及祖先结点依次是 $C[3]$、$C[4]$、$C[8]$ ，所以修改了 $A[3]$ 以后 $C[3]$、$C[4]$、$C[8]$ 的值也要修改。

先看 $C[3]​$ ，${\rm lowbit}(3) = 1​$， $3 + {\rm lowbit}(3) = 4​$ 就是 $C[3]​$ 的父亲结点 $C[4]​$ 的索引值。 再看 $C[4]​$ ，${\rm lowbit}(4) = 4​$， $4 + {\rm lowbit}(4) = 8​$ 就是 $C[4]​$ 的父亲结点 $C[8]​$ 的索引值。 从图中，也可以验证：“红色结点的索引值 + 右下角蓝色圆形结点的值 = 红色结点的双亲结点的索引值”。

下面我试图解释这个现象：$3$ 即 $0011$，从右向左，遇到 $0$ 放过，遇到 $1$ 为止，给这个数位加 $1$，这个操作就相当于加上了一个 $2^k$ 的二进制数，即一个 ${\rm lowbit}$ 值，有意思的事情就发生在此时，马上就发发生了进位，得到 $0100$，即 $4$ 的二进制表示。 接下来处理 $0100$，从右向左，从右向左，遇到 $0$ 放过，遇到 $1$ 为止，给这个数位加 $1$，同样地，这个操作就相当于加上了一个 $2^k$ 的二进制数，即一个 ${\rm lowbit}$ 值，可以看到，马上就发发生了进位，得到 $1000$，即 $8$ 的二进制表示。

从我上面的描述中，你可以发现，我们又在做“从右边到左边数，遇到 $1$ 之前数出 $0$ 的个数”这件事情了， 由此我们可以总结出规律：从已知子结点的索引 $i$ ，则结点 $i$ 的父结点的索引 ${\rm parent}$ 的计算公式为：

$$ {\rm parent}(i) = i + {\rm lowbit}(i) $$

可不过我还想说明的是，这不是巧合和循环论证，这正是因为对 “从右边到左边数出 $0$ 的个数，遇到 $1$ 停止这件事情”的定义，使用 ${\rm lowbit}$ 可以快速计算这件事成立，才会有的。

分析到这里“单点更新”的代码就可以马上写出来了。

可以看出“单点更新”和“前缀和查询操作”的代码量其实是很少的。

这里要说明的是，初始化前缀和数组应该交给调用者来决定。下面是一种初始化的方式。树状数组的初始化可以通过“单点更新”来实现，因为“最最开始”的时候，数组的每个元素的值都为 $0$，每个都对应地加上原始数组的值，就完成了预处理数组 $C$ 的创建。 这里要特别注意，update 操作的第 $2$ 个索引值是一个变化值，而不是变化以后的值。因为我们的操作是逐层上报，汇报变更值会让我们的操作更加简单，这一点请大家反复体会。