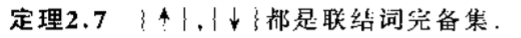| 离散数学之数理逻辑 | 您所在的位置:网站首页 › 析取范式变成合取范式的简单方法 › 离散数学之数理逻辑 |
离散数学之数理逻辑
|
1. 等值式
定义2.1 设A,B是两个命题公式,若A,B构成的等价式 A ↔ B A\leftrightarrow B A↔B为重言式,则称A与B是等值的,记作 A ⇔ B A\Leftrightarrow B A⇔B. ⇔ \Leftrightarrow ⇔不是连接符,它是用来说明A与B等值的一种记法,因而它是元语言符号。 本书给出16组重要的等值式,应牢牢记住: 上述16组等值式共包含了24个重要等值式。这样的等值式称为等值式模式,具体的等值式被称为原来等值式模式的待入实例 我们称由已知的等值式推演出另外一些等值式的过程为等值演算,等值演算是布尔代数或逻辑代数的重要组成部分。在等值演算过程中,要不断地使用一条重要的规则,它的内容如下: 置换规则 设 ϕ ( A ) \phi(A) ϕ(A)是含公式 A A A的命题公式, ϕ ( B ) \phi(B) ϕ(B)是用公式 B B B置换了 ϕ ( A ) \phi(A) ϕ(A)中所有的A后得到的命题公式,若 B ⇔ A B\Leftrightarrow A B⇔A,则 ϕ ( B ) ⇔ ϕ ( A ) \phi(B)\Leftrightarrow \phi(A) ϕ(B)⇔ϕ(A). 2. 析取范式与合取范式定义2.2 命题变项及其否定统称作文字。仅由有限个文字构成的析取式称作简单析取式。仅有有限个文字构成的合取式称作简单合取式 定理2.1 (1)一个简单析取式是重言式当且仅当它同时含某个命题变项及它的否定式 (2)一个简单合取式是矛盾式当且仅当它同时含某个命题变项及它的否定式 定义2.3 (1)由有限个简单合取式构成的析取式称为析取范式 (2)由有限个简单析取式构成的合取式称为合取范式 (3)析取范式与合取范式统称为范式 析取范式和合取范式有由下面定理给出的性质: 定理2.2 (1)一个析取范式是矛盾式当且仅当它的每个简单合取式都是矛盾式; (2)一个合取范式是重言式当且仅当它的每个简单析取式都是重言式; 由蕴含等值式与等价等值式、双重否定律和德摩根律、分配律 3步,可将任一公式化成与之等值的析取范式或合取范式。于是,下面的定理是正确的: 定理2.3 (范式存在定理) 任一命题公式都存在着与之等值的析取范式与合取范式。 下面给出求给定公式范式的步骤: 消去联结词(蕴含联结词、等价联结词);否定号的消去(利用双重否定律)或内移(利用德摩根律)利用分配律:利用“合取联 结词”对“析取联结词”的分配律求析取范式, “析取联结词”对“合取联结词”的分配律求合取范式。为了求出命题公式的唯一规范化形式的范式,必须先将简单合取式和简单析取式规范化。见下述定义 定义2.4 在含有n个命题变项的简单合取式(简单析取式)中,若每个命题变项和它的否定式不同时出现,而二者之一必须出现且仅出现一次,且第i个命题变项或它的否定式出现在从左算起的第i位上(若命题变项无角标,就按字典顺序排列),称这样的简单合取式(简单析取式)为极小项(极大项) 由于每个命题变项在极小项中以原形或否定式形式出现且仅出现一次,因而 n n n个命题变项共可产生 2 n 2^n 2n个不同的极小项。其中每个极小项都有且仅有一个成真赋值。若成真赋值所对应的二进制数转化为十进制数为 i i i,就将所对应的极小项记作 m i m_i mi,类似地, n n n个命题变项共可产生 2 n 2^n 2n个不同的极大项,每个极大项只有一个成假赋值,将其对应的十进制数i做极大项的角标,记作 M i M_i Mi。 为了便于记忆,将
p
,
q
p, q
p,q与
p
,
q
,
r
p, q, r
p,q,r形成的极小项和极大项分别列在表2.3和2.4上。 极小项与极大项有由下面定理给出的关系: 定理2.4 设 m i m_i mi与 M i M_i Mi是命题变项 p 1 , p 2 , ⋯ , p n p_1, p_2, \cdots, p_n p1,p2,⋯,pn形成的极小项和极大项,则 ¬ m i ⇔ M i , ¬ M i ⇔ m i \neg m_i \Leftrightarrow M_i, \neg M_i \Leftrightarrow m_i ¬mi⇔Mi,¬Mi⇔mi 定义2.5 设由n个命题变项构成的析取范式(合取范式)中所有的简单合取式(简单析取式)都是极小项(极大项),则称该析取范式(合取范式)为主析取范式(主合取范式) 下面要讨论的问题是,如何求出与给定公式等值的主析取范式和主合取范式,首先讨论它的存在性和唯一性,在讨论它的求法。 定理2.5 任何命题公式都存在着与之等值的主析取范式和主合取范式,并且是惟一的。 下面讨论主析取范式的用途(主合取范式可类似讨论)。公式的主析取范式像公式的真值表一样,可以表达出公式以及公式之间关系的一切信息。 求公式的成真与成假赋值判断公式的类型 设公式A中含n个命题变项,容易看出: (1)A为重言式当且仅当A的主析取范式含全部2的n次方个极小项; (2)A为矛盾式当且仅当A的主析取范式不含任何极小项,此时,记A的主析取范式为0; (3)A为可满足式当且仅当A的主析取范式中至少含有一个极小项。判断两个命题公式是否等值 设公式A,B共含有n个命题变项,按n个命题变项求出A与B的主析取范式A’与B’。若A’=B’,则AB,否则A与B不等值。应用主析取范式分析和解决实际问题以上主要讨论了主析取范式的求法与用途,对主合取范式还要说明以下两点: 由公式的主析取范式求主合取范式。 重言式与矛盾式的主合取范式。 矛盾式无成真赋值,因而矛盾式的主合取范式含2的n次方个极大项。而重言式无成假赋值,因而主合取范式不含任何极大项。将重言式的主合取范式记为1.至于可满足式,它的主合取范式中极大项的个数一定小于2的n次方。 最后,仍可以问这样的问题,含n个命题变项的所有无穷多的合式公式中,与他们等值的主析取范式(主合取范式)共有多少种不同的情况。n个命题变项共可产生2的n次方个极小项(极大项),因而共可产生: 种不同的主析取范式(主合取范式),由定理2.可知,含n个命题变项的所有公式的主析取范式(主合取范式)最多有2的 2的n次方 次方种不同的情况。这与在1.2节中对真值表个数的讨论情况是一样的,并且可以看出: A与B等值当且仅当A与B有相同的真值表,又当且仅当A与B有 相同的主析取范式(主合取范式)。因而可以这样说,真值表与主析取范式(主合取范式)是描述命题公式标准的两种不同的等价形式。 3. 联结词的完备集定义2.6 定理2.6 S={非,且,或}是联结词完备集。 推论 以下联结词集都是完备集: (1)S1 = {非,且,或,蕴含} (2)S2 = {非,且,或,蕴含,等价} (3)S3 = {非,且} (4)S4 = {非,或} (5)S5 = {非,蕴含} 定义2.8 设p、q为两个命题,复合命题“p与q的否定式”(“p或q的否定式”)称作p,q的与非式(或非式),记作 定理2.7 |
【本文地址】




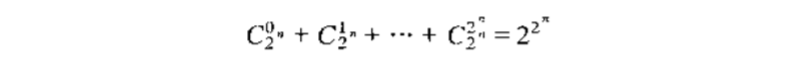
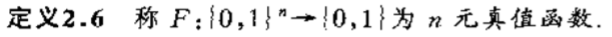 定义2.7 设S是一个联结词集合,如果任何n(n>=1)元真值函数都可以由仅含S中的联结词构成的公式表示,则称S是联接词完备集
定义2.7 设S是一个联结词集合,如果任何n(n>=1)元真值函数都可以由仅含S中的联结词构成的公式表示,则称S是联接词完备集