|
推断(Inference) 这个词,对于有一定机器学习基础的同学来说,一定是听说过,这也是贝叶斯方法中一个非常重要的理论性研究。那么什么是推断呢?推断说白了,就是求概率。比如,对于一个联合概率密度函数
p
(
x
)
=
p
(
x
1
,
x
2
,
⋯
,
x
p
)
p(x) = p(x_1,x_2,\cdots,x_p)
p(x)=p(x1,x2,⋯,xp)。我们需要求的有哪些呢?
边缘概率:
p
(
x
i
)
=
∑
x
1
⋯
∑
x
i
−
1
⋯
∑
x
i
+
1
⋯
∑
x
p
p
(
x
)
p\left(x_{i}\right)=\sum_{x_{1}} \cdots \sum_{x_{i-1}} \cdots \sum_{x_{i+1}} \cdots \sum_{x_{p}} p(x)
p(xi)=∑x1⋯∑xi−1⋯∑xi+1⋯∑xpp(x)条件概率:
p
(
x
A
∣
x
B
)
,
p\left(x_{A} | x_{B}\right),
p(xA∣xB), 今
x
=
x
A
∪
x
B
x=x_{A} \cup x_{B}
x=xA∪xBMAP Inference:也就是
z
^
=
arg
max
z
p
(
z
∣
x
)
∝
argmax
p
(
x
,
z
)
\hat{z}=\arg \max _{z} p(z | x) \propto \operatorname{argmax} p(x, z)
z^=argmaxzp(z∣x)∝argmaxp(x,z) 因为,
p
(
z
∣
x
)
=
p
(
x
,
z
)
p
(
x
)
∝
p
(
x
,
z
)
p(z | x)=\frac{p(x, z)}{p(x)} \propto p(x, z)
p(z∣x)=p(x)p(x,z)∝p(x,z)
因为我们的目标是求一个最优的参数z,并不需要知道具体的数值是多少,只要知道谁大谁小就行,所以
p
(
x
)
p(x)
p(x) 可以直接不看了。 现在我们知道了,Inference 在求什么?下一步,我们要总结Inference 有哪些方法。
1 背景
1.1 Inference 求解方法
1.1.1 精准推断(Deterministic Inference)
Variable Elimination (VE),变量消除法;Belief Propagation (BP) 信念传播,这个可不是我们之前学习的反向传播算法,这里需要注意。同时这个算法衍生出的Sum Product Algorithm,这就是推断的核心,这是一种树结构的;Junction Tree Algorithm,这是一种普通图结构。
1.1.2 近似推断(Approximate Inference)
典型的有有向环(Loop Belief Propagation);采样方法,包括Mente Carlo Inference:Importance Sampling,MCMC;变分推断(Variational Inference)。
1.2 隐马尔可夫模型(Hidden Markov Model)
 Hidden Markov Model (HMM) 算法将在后面的章节中做详细的描述,在这一小节中,我们主要做一点概述性的描述。HMM 的模型可视化为上图所示,其中O 是隐变量,也就是我们的观测变量。 我们主要考虑三个问题,在三个问题为Inference 的问题。1. Evaluation,也就是求一个边缘密度
p
(
O
)
=
∑
I
P
(
I
,
O
)
p(O)=\sum_{I} P(I, O)
p(O)=∑IP(I,O)。2. Learning,也就是寻找
λ
^
∘
\hat{\lambda}_{\circ}
λ^∘ 3. Decoding:
I
^
=
argmax
I
P
(
I
∣
O
)
\hat{I}=\operatorname{argmax}_{I} P(I | O)
I^=argmaxIP(I∣O),包括Vitebi Algorithm,这是一个动态规划算法。而隐马尔可夫模型实际上一种动态规划模型(Dynamic Bayesian Network)。 Hidden Markov Model (HMM) 算法将在后面的章节中做详细的描述,在这一小节中,我们主要做一点概述性的描述。HMM 的模型可视化为上图所示,其中O 是隐变量,也就是我们的观测变量。 我们主要考虑三个问题,在三个问题为Inference 的问题。1. Evaluation,也就是求一个边缘密度
p
(
O
)
=
∑
I
P
(
I
,
O
)
p(O)=\sum_{I} P(I, O)
p(O)=∑IP(I,O)。2. Learning,也就是寻找
λ
^
∘
\hat{\lambda}_{\circ}
λ^∘ 3. Decoding:
I
^
=
argmax
I
P
(
I
∣
O
)
\hat{I}=\operatorname{argmax}_{I} P(I | O)
I^=argmaxIP(I∣O),包括Vitebi Algorithm,这是一个动态规划算法。而隐马尔可夫模型实际上一种动态规划模型(Dynamic Bayesian Network)。
2 变量消除:Variable Elimination
在上一小节中,我们简单的介绍了推断的背景和分类,我们知道了大致有哪些推断的方法。推断的任务可以被我们介绍为:给定已知的
p
(
x
)
=
p
(
x
1
,
x
2
,
⋯
,
x
p
)
p(x) = p(x_1,x_2,\cdots,x_p)
p(x)=p(x1,x2,⋯,xp),我们需要求的有三个:
边缘概率:
p
(
x
i
)
=
∑
x
1
,
⋯
,
x
i
−
1
,
x
i
+
1
,
⋯
,
x
p
p
(
x
1
,
x
2
,
⋯
,
x
p
)
p\left(x_{i}\right)=\sum_{x_{1}, \cdots, x_{i-1}, x_{i+1}, \cdots, x_{p}} p\left(x_{1}, x_{2}, \cdots, x_{p}\right)
p(xi)=∑x1,⋯,xi−1,xi+1,⋯,xpp(x1,x2,⋯,xp)条件概率:
p
(
x
A
∣
x
B
)
p(x_A|x_B)
p(xA∣xB),也就是在已知
x
B
x_B
xB 集合的情况下,如何求得xA 集合的概率。最大后验概率(MAP):
x
^
A
=
argmax
x
A
p
(
x
A
∣
x
B
)
=
argmax
p
(
x
A
,
x
B
)
\hat{x}_{A}=\operatorname{argmax}_{x_{A}} p\left(x_{A} | x_{B}\right)=\operatorname{argmax} p\left(x_{A}, x_{B}\right)
x^A=argmaxxAp(xA∣xB)=argmaxp(xA,xB)。 下面我们要介绍最简单的一个精确推断中中的东西,名为变量消除法(Variable Elimination)。这是一种最简单的推断方法,也是我们学习推断法的核心概念之一。下面我们做详细的解释。
2.1变量消除法(Variable Elimination Algorithm)
假如我们有一个马氏链: 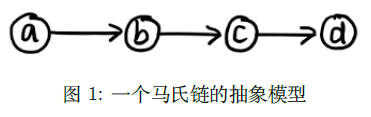 那么我们怎么来求
p
(
d
)
p(d)
p(d) 呢?根据公式我们可以得到:
p
(
d
)
=
∑
a
,
b
,
c
p
(
a
,
b
,
c
,
d
)
p(d)=\sum_{a,b,c}p(a,b,c,d)
p(d)=a,b,c∑p(a,b,c,d) 然后使用因子分解,我们可以得到:
p
(
d
)
=
∑
a
,
b
,
c
p
(
a
)
p
(
b
∣
a
)
p
(
c
∣
b
)
p
(
d
∣
c
)
p(d)=\sum_{a,b,c}p(a)p(b|a)p(c|b)p(d|c)
p(d)=a,b,c∑p(a)p(b∣a)p(c∣b)p(d∣c) 假定,
a
,
b
,
c
,
d
a,b,c,d
a,b,c,d 都为均匀离散的二值random variable,所以
a
,
b
,
c
,
d
∈
a,b,c,d\in
a,b,c,d∈ {0,1}。 所以,
p
(
d
)
=
p
(
a
=
0
)
⋅
p
(
b
=
0
∣
a
=
0
)
⋅
p
(
c
=
0
∣
b
=
0
)
⋅
p
(
d
∣
c
=
0
)
+
p
(
a
=
1
)
⋅
p
(
b
=
0
∣
a
=
1
)
⋅
p
(
c
=
0
∣
b
=
0
)
⋅
p
(
d
∣
c
=
0
)
+
⋯
+
p
(
a
=
1
)
⋅
p
(
b
=
1
∣
a
=
1
)
⋅
p
(
c
=
1
∣
b
=
1
)
⋅
p
(
d
∣
c
=
1
)
\begin{aligned} p(d) &=p(a = 0) \cdot p(b = 0|a = 0) \cdot p(c = 0|b = 0) \cdot p(d|c = 0) \\ & +p(a = 1) \cdot p(b = 0|a = 1) \cdot p(c = 0|b = 0) \cdot p(d|c = 0) \\ &+\cdots \\ &+p(a = 1) \cdot p(b = 1|a = 1) \cdot p(c = 1|b = 1) \cdot p(d|c = 1) \end{aligned}
p(d)=p(a=0)⋅p(b=0∣a=0)⋅p(c=0∣b=0)⋅p(d∣c=0)+p(a=1)⋅p(b=0∣a=1)⋅p(c=0∣b=0)⋅p(d∣c=0)+⋯+p(a=1)⋅p(b=1∣a=1)⋅p(c=1∣b=1)⋅p(d∣c=1) 实际上,这里有8 个因子的积。那么我们来做进一步的分析,我们可以令
p
(
d
)
=
∑
a
,
b
,
c
p
(
a
)
p
(
b
∣
a
)
p
(
c
∣
b
)
p
(
d
∣
c
)
=
∑
b
,
c
p
(
c
∣
b
)
p
(
d
∣
c
)
∑
a
p
(
a
)
p
(
b
∣
a
)
\begin{aligned} p(d) &=\sum_{a,b,c}p(a)p(b|a)p(c|b)p(d|c) \\ & =\sum_{b,c}p(c|b)p(d|c)\sum_{a}p(a)p(b|a) \end{aligned}
p(d)=a,b,c∑p(a)p(b∣a)p(c∣b)p(d∣c)=b,c∑p(c∣b)p(d∣c)a∑p(a)p(b∣a) 而
p
(
a
)
p
(
b
∣
a
)
=
p
(
a
,
b
)
p(a)p(b|a) = p(a,b)
p(a)p(b∣a)=p(a,b),而
∑
a
p
(
a
)
p
(
b
∣
a
)
=
p
(
b
)
\sum_a p(a)p(b|a) = p(b)
∑ap(a)p(b∣a)=p(b)。我们可以将
a
a
a 看成
ϕ
(
a
)
ϕ(a)
ϕ(a) 这是一个和
a
a
a 相关的函数,同理
p
(
b
∣
a
)
p(b|a)
p(b∣a)看成
ϕ
(
a
,
b
)
ϕ(a, b)
ϕ(a,b)。所以,我们可以将
∑
a
p
(
a
)
p
(
b
∣
a
)
\sum_a p(a)p(b|a)
∑ap(a)p(b∣a) 看成
ϕ
a
(
b
)
ϕ_a(b)
ϕa(b),这样就相当于一个关于
b
b
b 的函数,并且是从
a
a
a 中导出的。所以,我们做如下替换可得:
∑
b
,
c
p
(
c
∣
b
)
p
(
d
∣
c
)
∑
a
p
(
a
)
p
(
b
∣
a
)
=
∑
b
,
c
p
(
c
∣
b
)
p
(
d
∣
c
)
ϕ
a
b
=
∑
c
p
(
d
∣
c
)
∑
b
p
(
c
∣
b
)
ϕ
a
b
\sum_{b,c}p(c|b)p(d|c)\sum_{a}p(a)p(b|a)=\sum_{b,c}p(c|b)p(d|c)ϕ_{a}b=\sum_{c}p(d|c)\sum_{b}p(c|b)ϕ_{a}b
b,c∑p(c∣b)p(d∣c)a∑p(a)p(b∣a)=b,c∑p(c∣b)p(d∣c)ϕab=c∑p(d∣c)b∑p(c∣b)ϕab 同理,我们将
∑
b
p
(
c
∣
b
)
ϕ
a
b
\sum_{b}p(c|b)ϕ_{a}b
∑bp(c∣b)ϕab 看成
ϕ
b
(
c
)
ϕ_b(c)
ϕb(c)。所以,原始将被改写为:
∑
c
p
(
d
∣
c
)
ϕ
b
(
c
)
=
ϕ
b
(
c
)
\sum_{c}p(d|c)ϕ_b(c)=ϕ_b(c)
c∑p(d∣c)ϕb(c)=ϕb(c) 这个算法的核心就是乘法对加法的分配律。那我们怎么类比到乘法的分配律呢?首先先来简单的回顾一下乘法的分配律,也就是
a
c
+
a
b
=
a
(
b
+
c
)
ac+ab = a(b+c)
ac+ab=a(b+c)。那么我们仔细的来看看这个计算p(d) 的过程。这是不是就是一个不断的提取公因子,进行计算的过程?有没有觉得和分配律很像?先提取
a
a
a 的部分,计算
a
a
a 的部分,然后再依次的提取
b
b
b 的部分,
c
c
c 的部分,最后剩下的就是
d
d
d 的部分。那么,我们就可以把这么一长串的公式进行逐步化简了,这就是变量消元的思想。同样,在无向图中,我们也可以使用到马尔可夫网络中。
p
(
a
,
b
,
c
,
d
)
=
1
z
∏
i
=
1
k
ϕ
c
i
(
x
c
i
)
p ( a , b , c , d ) = \frac { 1 } { z } \prod _ { i = 1 } ^ { k } \phi _ { c _ { i } } ( x _ { c _ { i } } )
p(a,b,c,d)=z1i=1∏kϕci(xci) 写成因子分解的形式就是
p
(
x
)
=
∏
x
i
ϕ
i
(
x
i
)
p ( x ) = \prod _ { x _ { i } } \phi _ { i } ( x _ { i } )
p(x)=xi∏ϕi(xi) 这实际上就是分配律,一个变量一个变量的提取,然后进行分解计算。同时这种算法的缺点也非常的明显。 首先,就是重复计算的问题,无论计算那个变量的概率都要重复的计算一遍所有的概率。这个原因就会导致算法的计算难度非常的大。第二个就是计算次序的问题,我们举的例子还比较的简单,所以我们可以一眼就看出来,按
a
−
b
−
c
−
d
a - b - c - d
a−b−c−d 的次序开始算。但是,实际上,并没有这么容易就得到计算的次序,而且计算次序不一样会导致计算的难度有很大的区别。而有数学家已经证明了,确定最优的计算顺序,本身就是一个NP hard 的问题,非常难求解。 那么我们怎么来求
p
(
d
)
p(d)
p(d) 呢?根据公式我们可以得到:
p
(
d
)
=
∑
a
,
b
,
c
p
(
a
,
b
,
c
,
d
)
p(d)=\sum_{a,b,c}p(a,b,c,d)
p(d)=a,b,c∑p(a,b,c,d) 然后使用因子分解,我们可以得到:
p
(
d
)
=
∑
a
,
b
,
c
p
(
a
)
p
(
b
∣
a
)
p
(
c
∣
b
)
p
(
d
∣
c
)
p(d)=\sum_{a,b,c}p(a)p(b|a)p(c|b)p(d|c)
p(d)=a,b,c∑p(a)p(b∣a)p(c∣b)p(d∣c) 假定,
a
,
b
,
c
,
d
a,b,c,d
a,b,c,d 都为均匀离散的二值random variable,所以
a
,
b
,
c
,
d
∈
a,b,c,d\in
a,b,c,d∈ {0,1}。 所以,
p
(
d
)
=
p
(
a
=
0
)
⋅
p
(
b
=
0
∣
a
=
0
)
⋅
p
(
c
=
0
∣
b
=
0
)
⋅
p
(
d
∣
c
=
0
)
+
p
(
a
=
1
)
⋅
p
(
b
=
0
∣
a
=
1
)
⋅
p
(
c
=
0
∣
b
=
0
)
⋅
p
(
d
∣
c
=
0
)
+
⋯
+
p
(
a
=
1
)
⋅
p
(
b
=
1
∣
a
=
1
)
⋅
p
(
c
=
1
∣
b
=
1
)
⋅
p
(
d
∣
c
=
1
)
\begin{aligned} p(d) &=p(a = 0) \cdot p(b = 0|a = 0) \cdot p(c = 0|b = 0) \cdot p(d|c = 0) \\ & +p(a = 1) \cdot p(b = 0|a = 1) \cdot p(c = 0|b = 0) \cdot p(d|c = 0) \\ &+\cdots \\ &+p(a = 1) \cdot p(b = 1|a = 1) \cdot p(c = 1|b = 1) \cdot p(d|c = 1) \end{aligned}
p(d)=p(a=0)⋅p(b=0∣a=0)⋅p(c=0∣b=0)⋅p(d∣c=0)+p(a=1)⋅p(b=0∣a=1)⋅p(c=0∣b=0)⋅p(d∣c=0)+⋯+p(a=1)⋅p(b=1∣a=1)⋅p(c=1∣b=1)⋅p(d∣c=1) 实际上,这里有8 个因子的积。那么我们来做进一步的分析,我们可以令
p
(
d
)
=
∑
a
,
b
,
c
p
(
a
)
p
(
b
∣
a
)
p
(
c
∣
b
)
p
(
d
∣
c
)
=
∑
b
,
c
p
(
c
∣
b
)
p
(
d
∣
c
)
∑
a
p
(
a
)
p
(
b
∣
a
)
\begin{aligned} p(d) &=\sum_{a,b,c}p(a)p(b|a)p(c|b)p(d|c) \\ & =\sum_{b,c}p(c|b)p(d|c)\sum_{a}p(a)p(b|a) \end{aligned}
p(d)=a,b,c∑p(a)p(b∣a)p(c∣b)p(d∣c)=b,c∑p(c∣b)p(d∣c)a∑p(a)p(b∣a) 而
p
(
a
)
p
(
b
∣
a
)
=
p
(
a
,
b
)
p(a)p(b|a) = p(a,b)
p(a)p(b∣a)=p(a,b),而
∑
a
p
(
a
)
p
(
b
∣
a
)
=
p
(
b
)
\sum_a p(a)p(b|a) = p(b)
∑ap(a)p(b∣a)=p(b)。我们可以将
a
a
a 看成
ϕ
(
a
)
ϕ(a)
ϕ(a) 这是一个和
a
a
a 相关的函数,同理
p
(
b
∣
a
)
p(b|a)
p(b∣a)看成
ϕ
(
a
,
b
)
ϕ(a, b)
ϕ(a,b)。所以,我们可以将
∑
a
p
(
a
)
p
(
b
∣
a
)
\sum_a p(a)p(b|a)
∑ap(a)p(b∣a) 看成
ϕ
a
(
b
)
ϕ_a(b)
ϕa(b),这样就相当于一个关于
b
b
b 的函数,并且是从
a
a
a 中导出的。所以,我们做如下替换可得:
∑
b
,
c
p
(
c
∣
b
)
p
(
d
∣
c
)
∑
a
p
(
a
)
p
(
b
∣
a
)
=
∑
b
,
c
p
(
c
∣
b
)
p
(
d
∣
c
)
ϕ
a
b
=
∑
c
p
(
d
∣
c
)
∑
b
p
(
c
∣
b
)
ϕ
a
b
\sum_{b,c}p(c|b)p(d|c)\sum_{a}p(a)p(b|a)=\sum_{b,c}p(c|b)p(d|c)ϕ_{a}b=\sum_{c}p(d|c)\sum_{b}p(c|b)ϕ_{a}b
b,c∑p(c∣b)p(d∣c)a∑p(a)p(b∣a)=b,c∑p(c∣b)p(d∣c)ϕab=c∑p(d∣c)b∑p(c∣b)ϕab 同理,我们将
∑
b
p
(
c
∣
b
)
ϕ
a
b
\sum_{b}p(c|b)ϕ_{a}b
∑bp(c∣b)ϕab 看成
ϕ
b
(
c
)
ϕ_b(c)
ϕb(c)。所以,原始将被改写为:
∑
c
p
(
d
∣
c
)
ϕ
b
(
c
)
=
ϕ
b
(
c
)
\sum_{c}p(d|c)ϕ_b(c)=ϕ_b(c)
c∑p(d∣c)ϕb(c)=ϕb(c) 这个算法的核心就是乘法对加法的分配律。那我们怎么类比到乘法的分配律呢?首先先来简单的回顾一下乘法的分配律,也就是
a
c
+
a
b
=
a
(
b
+
c
)
ac+ab = a(b+c)
ac+ab=a(b+c)。那么我们仔细的来看看这个计算p(d) 的过程。这是不是就是一个不断的提取公因子,进行计算的过程?有没有觉得和分配律很像?先提取
a
a
a 的部分,计算
a
a
a 的部分,然后再依次的提取
b
b
b 的部分,
c
c
c 的部分,最后剩下的就是
d
d
d 的部分。那么,我们就可以把这么一长串的公式进行逐步化简了,这就是变量消元的思想。同样,在无向图中,我们也可以使用到马尔可夫网络中。
p
(
a
,
b
,
c
,
d
)
=
1
z
∏
i
=
1
k
ϕ
c
i
(
x
c
i
)
p ( a , b , c , d ) = \frac { 1 } { z } \prod _ { i = 1 } ^ { k } \phi _ { c _ { i } } ( x _ { c _ { i } } )
p(a,b,c,d)=z1i=1∏kϕci(xci) 写成因子分解的形式就是
p
(
x
)
=
∏
x
i
ϕ
i
(
x
i
)
p ( x ) = \prod _ { x _ { i } } \phi _ { i } ( x _ { i } )
p(x)=xi∏ϕi(xi) 这实际上就是分配律,一个变量一个变量的提取,然后进行分解计算。同时这种算法的缺点也非常的明显。 首先,就是重复计算的问题,无论计算那个变量的概率都要重复的计算一遍所有的概率。这个原因就会导致算法的计算难度非常的大。第二个就是计算次序的问题,我们举的例子还比较的简单,所以我们可以一眼就看出来,按
a
−
b
−
c
−
d
a - b - c - d
a−b−c−d 的次序开始算。但是,实际上,并没有这么容易就得到计算的次序,而且计算次序不一样会导致计算的难度有很大的区别。而有数学家已经证明了,确定最优的计算顺序,本身就是一个NP hard 的问题,非常难求解。
3 Belief Propagation:信念传播
在上一小节中,我们已经介绍了变量消除(Variable Elimination),Variable Elimination 的思想是 Probability Graph 中的核心思想之一。上一节中我们就已经介绍了,这实际上就是乘法对加法的分配律。但是,Variable Elimination 中有很多的问题,比如重复计算和最优计算次序不好确定的问题。所以,我们这一节来介绍Belief Propagation 来解决重复计算的问题。
3.1 Forward and Backward Algorithm
假设,我们现在有一个马氏链模型: 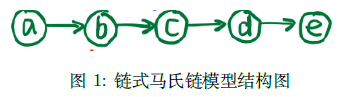 联合概率可以被我们表示为:
p
(
a
,
b
,
c
,
d
,
e
)
=
p
(
a
)
⋅
p
(
b
∣
a
)
⋅
p
(
c
∣
b
)
⋅
p
(
d
∣
c
)
⋅
p
(
e
∣
d
)
p(a, b, c, d, e) = p(a) \cdot p(b|a) \cdot p(c|b) \cdot p(d|c) \cdot p(e|d)
p(a,b,c,d,e)=p(a)⋅p(b∣a)⋅p(c∣b)⋅p(d∣c)⋅p(e∣d)。 如果,我们想要求的是
p
(
e
)
p(e)
p(e),那么:
p
(
e
)
=
∑
a
,
b
,
c
,
d
p
(
a
,
b
,
c
,
d
,
e
)
=
∑
a
p
(
e
∣
d
)
⋅
∑
c
p
(
d
∣
c
)
⋅
∑
b
p
(
c
∣
b
)
⋅
∑
a
p
(
b
∣
a
)
⋅
p
(
a
)
\left. \begin{array}{l}{ p ( e ) = \sum _ { a , b , c , d } p ( a , b , c , d , e ) }\\ \\{ = \sum _ { a } p ( e | d ) \cdot \sum _ { c } p ( d | c ) \cdot \sum _ { b } p ( c | b ) \cdot \sum _ { a } p ( b | a ) \cdot p ( a ) }\end{array} \right.
p(e)=∑a,b,c,dp(a,b,c,d,e)=∑ap(e∣d)⋅∑cp(d∣c)⋅∑bp(c∣b)⋅∑ap(b∣a)⋅p(a) 为了简化表达,这里我们需要定义一个很重要的符号。因为
∑
a
p
(
b
∣
a
)
⋅
p
(
a
)
\sum _ { a } p ( b | a ) \cdot p ( a )
∑ap(b∣a)⋅p(a),是一个关于b 的表达式,也就是相当于把a 给约掉了。所以我们可以把
∑
a
p
(
b
∣
a
)
⋅
p
(
a
)
\sum _ { a } p ( b | a ) \cdot p ( a )
∑ap(b∣a)⋅p(a)记为
m
a
→
b
(
b
)
m _ { a \rightarrow b } ( b )
ma→b(b)。同理,我们也可以将
∑
c
p
(
d
∣
c
)
⋅
∑
b
p
(
c
∣
b
)
⋅
m
a
→
b
(
b
)
\sum _ { c } p ( d | c ) \cdot \sum _ { b } p ( c | b ) \cdot m _ { a \rightarrow b } ( b )
∑cp(d∣c)⋅∑bp(c∣b)⋅ma→b(b)记为
m
b
→
c
(
c
)
m _ { b \rightarrow c } ( c )
mb→c(c)。那么为了求得p(e),我们依次的求解顺序为
m
a
→
b
(
b
)
m _ { a \rightarrow b } ( b )
ma→b(b),
m
b
→
c
(
c
)
m _ { b \rightarrow c } ( c )
mb→c(c),
m
c
→
d
(
d
)
m _ { c \rightarrow d } ( d )
mc→d(d)和
m
d
→
e
(
e
)
m _ { d \rightarrow e } ( e )
md→e(e)。也就相当于沿着这个链这个马氏链一直往前走,也就是前向算法(Forward Algorithm)。我们用公式表达即为: 联合概率可以被我们表示为:
p
(
a
,
b
,
c
,
d
,
e
)
=
p
(
a
)
⋅
p
(
b
∣
a
)
⋅
p
(
c
∣
b
)
⋅
p
(
d
∣
c
)
⋅
p
(
e
∣
d
)
p(a, b, c, d, e) = p(a) \cdot p(b|a) \cdot p(c|b) \cdot p(d|c) \cdot p(e|d)
p(a,b,c,d,e)=p(a)⋅p(b∣a)⋅p(c∣b)⋅p(d∣c)⋅p(e∣d)。 如果,我们想要求的是
p
(
e
)
p(e)
p(e),那么:
p
(
e
)
=
∑
a
,
b
,
c
,
d
p
(
a
,
b
,
c
,
d
,
e
)
=
∑
a
p
(
e
∣
d
)
⋅
∑
c
p
(
d
∣
c
)
⋅
∑
b
p
(
c
∣
b
)
⋅
∑
a
p
(
b
∣
a
)
⋅
p
(
a
)
\left. \begin{array}{l}{ p ( e ) = \sum _ { a , b , c , d } p ( a , b , c , d , e ) }\\ \\{ = \sum _ { a } p ( e | d ) \cdot \sum _ { c } p ( d | c ) \cdot \sum _ { b } p ( c | b ) \cdot \sum _ { a } p ( b | a ) \cdot p ( a ) }\end{array} \right.
p(e)=∑a,b,c,dp(a,b,c,d,e)=∑ap(e∣d)⋅∑cp(d∣c)⋅∑bp(c∣b)⋅∑ap(b∣a)⋅p(a) 为了简化表达,这里我们需要定义一个很重要的符号。因为
∑
a
p
(
b
∣
a
)
⋅
p
(
a
)
\sum _ { a } p ( b | a ) \cdot p ( a )
∑ap(b∣a)⋅p(a),是一个关于b 的表达式,也就是相当于把a 给约掉了。所以我们可以把
∑
a
p
(
b
∣
a
)
⋅
p
(
a
)
\sum _ { a } p ( b | a ) \cdot p ( a )
∑ap(b∣a)⋅p(a)记为
m
a
→
b
(
b
)
m _ { a \rightarrow b } ( b )
ma→b(b)。同理,我们也可以将
∑
c
p
(
d
∣
c
)
⋅
∑
b
p
(
c
∣
b
)
⋅
m
a
→
b
(
b
)
\sum _ { c } p ( d | c ) \cdot \sum _ { b } p ( c | b ) \cdot m _ { a \rightarrow b } ( b )
∑cp(d∣c)⋅∑bp(c∣b)⋅ma→b(b)记为
m
b
→
c
(
c
)
m _ { b \rightarrow c } ( c )
mb→c(c)。那么为了求得p(e),我们依次的求解顺序为
m
a
→
b
(
b
)
m _ { a \rightarrow b } ( b )
ma→b(b),
m
b
→
c
(
c
)
m _ { b \rightarrow c } ( c )
mb→c(c),
m
c
→
d
(
d
)
m _ { c \rightarrow d } ( d )
mc→d(d)和
m
d
→
e
(
e
)
m _ { d \rightarrow e } ( e )
md→e(e)。也就相当于沿着这个链这个马氏链一直往前走,也就是前向算法(Forward Algorithm)。我们用公式表达即为:  如果是要求
p
(
c
)
p(c)
p(c),那么我们的传递过程为
a
→
b
→
c
←
d
←
e
a \rightarrow b\rightarrow c \leftarrow d\leftarrow e
a→b→c←d←e。这里,我们就不能只用前向算法来解决了,需要用到Forward-Backward 算法来解决了。也就是同时使用Forward 和Backward的方法,那么我们来看看
p
(
c
)
p(c)
p(c)怎么求?
p
(
c
)
=
∑
a
,
b
,
d
,
e
p
(
a
,
b
,
c
,
d
,
e
)
=
(
∑
b
p
(
c
∣
b
)
∑
a
p
(
b
∣
a
)
p
(
a
)
)
⋅
(
∑
d
p
(
d
∣
c
)
∑
e
p
(
e
∣
d
)
)
\begin{aligned} p ( c ) &= \sum _ { a , b , d , e } p ( a , b , c , d , e ) \\ \\ &= ( \sum _ { b } p ( c | b ) \sum _ { a } p ( b | a ) p ( a ) ) \cdot ( \sum _ { d } p ( d | c ) \sum _ { e } p ( e | d ) ) \end{aligned}
p(c)=a,b,d,e∑p(a,b,c,d,e)=(b∑p(c∣b)a∑p(b∣a)p(a))⋅(d∑p(d∣c)e∑p(e∣d)) 对比上面的计算
p
(
e
)
p(e)
p(e) 的过程,我们就可以发现,
∑
b
p
(
c
∣
b
)
∑
a
p
(
b
∣
a
)
p
(
a
)
\sum_{b} p ( c | b ) \sum_{a} p ( b | a ) p ( a )
∑bp(c∣b)∑ap(b∣a)p(a)部分的计算也就是
m
b
→
c
(
c
)
m _ { b \rightarrow c } ( c )
mb→c(c)的计算是一模一样的。所以说,Variable Elimination 里面有大量的重复计算。Belief 的想法很简单,也就是将
m
i
→
j
(
j
)
m _ { i \rightarrow j } ( j )
mi→j(j),全部事先计算好,就像一个个积木一样,然后再用这个积木来搭建运算。那么也就是,我们事先将方向全部定义好,正向和反向的全部都求了再说。为了进一步探究Belief Background,我们需要讨论一些更加Generalize 的情况。也就是从
C
h
a
i
n
→
T
r
e
e
Chain \rightarrow Tree
Chain→Tree,有向
→
\rightarrow
→无项的情况。 如果是要求
p
(
c
)
p(c)
p(c),那么我们的传递过程为
a
→
b
→
c
←
d
←
e
a \rightarrow b\rightarrow c \leftarrow d\leftarrow e
a→b→c←d←e。这里,我们就不能只用前向算法来解决了,需要用到Forward-Backward 算法来解决了。也就是同时使用Forward 和Backward的方法,那么我们来看看
p
(
c
)
p(c)
p(c)怎么求?
p
(
c
)
=
∑
a
,
b
,
d
,
e
p
(
a
,
b
,
c
,
d
,
e
)
=
(
∑
b
p
(
c
∣
b
)
∑
a
p
(
b
∣
a
)
p
(
a
)
)
⋅
(
∑
d
p
(
d
∣
c
)
∑
e
p
(
e
∣
d
)
)
\begin{aligned} p ( c ) &= \sum _ { a , b , d , e } p ( a , b , c , d , e ) \\ \\ &= ( \sum _ { b } p ( c | b ) \sum _ { a } p ( b | a ) p ( a ) ) \cdot ( \sum _ { d } p ( d | c ) \sum _ { e } p ( e | d ) ) \end{aligned}
p(c)=a,b,d,e∑p(a,b,c,d,e)=(b∑p(c∣b)a∑p(b∣a)p(a))⋅(d∑p(d∣c)e∑p(e∣d)) 对比上面的计算
p
(
e
)
p(e)
p(e) 的过程,我们就可以发现,
∑
b
p
(
c
∣
b
)
∑
a
p
(
b
∣
a
)
p
(
a
)
\sum_{b} p ( c | b ) \sum_{a} p ( b | a ) p ( a )
∑bp(c∣b)∑ap(b∣a)p(a)部分的计算也就是
m
b
→
c
(
c
)
m _ { b \rightarrow c } ( c )
mb→c(c)的计算是一模一样的。所以说,Variable Elimination 里面有大量的重复计算。Belief 的想法很简单,也就是将
m
i
→
j
(
j
)
m _ { i \rightarrow j } ( j )
mi→j(j),全部事先计算好,就像一个个积木一样,然后再用这个积木来搭建运算。那么也就是,我们事先将方向全部定义好,正向和反向的全部都求了再说。为了进一步探究Belief Background,我们需要讨论一些更加Generalize 的情况。也就是从
C
h
a
i
n
→
T
r
e
e
Chain \rightarrow Tree
Chain→Tree,有向
→
\rightarrow
→无项的情况。
3.2 Belief Propagation 的扩展
我们的Generalize 的后,分析了一个树形的无向图结构。图的网络结构如下所示:  下面第一步,我们把上面那个模型的设置写出来。所以,我们需要进行因式分解,我们用
φ
(
i
)
φ(i)
φ(i)来表示和
i
i
i 有关的部分。所以,我们可以将联合概率密度写为:
p
(
a
,
b
,
c
,
d
)
=
1
Z
φ
a
(
a
)
φ
b
(
b
)
φ
c
(
c
)
φ
d
(
d
)
⋅
φ
a
,
b
(
a
,
b
)
φ
b
,
c
(
b
,
c
)
φ
(
b
,
d
)
(
b
,
d
)
p ( a , b , c , d ) = \frac { 1 } { Z } \varphi _ { a } ( a ) \varphi _ { b } ( b ) \varphi _ { c } ( c ) \varphi _ { d } ( d ) \cdot \varphi _ { a , b } ( a , b ) \varphi _ { b , c } ( b , c ) \varphi ( b , d ) ( b , d )
p(a,b,c,d)=Z1φa(a)φb(b)φc(c)φd(d)⋅φa,b(a,b)φb,c(b,c)φ(b,d)(b,d) 我们要求
p
(
a
)
=
∑
b
,
c
,
d
p
(
a
,
b
,
c
,
d
)
p(a) =\sum_{b,c,d} p(a,b,c,d)
p(a)=∑b,c,dp(a,b,c,d)和
p
(
b
)
=
∑
a
,
c
,
d
p
(
a
,
b
,
c
,
d
)
p(b) =\sum_{a,c,d} p(a,b,c,d)
p(b)=∑a,c,dp(a,b,c,d),其间一定会出现大量的重复计算。这个模型中有四个点,三条边,每条边都有两个方向,所以我们要求的是6 个“积木”。我们来一步步 的看看,如何可以得到想要的
p
(
a
)
p(a)
p(a)。 下面第一步,我们把上面那个模型的设置写出来。所以,我们需要进行因式分解,我们用
φ
(
i
)
φ(i)
φ(i)来表示和
i
i
i 有关的部分。所以,我们可以将联合概率密度写为:
p
(
a
,
b
,
c
,
d
)
=
1
Z
φ
a
(
a
)
φ
b
(
b
)
φ
c
(
c
)
φ
d
(
d
)
⋅
φ
a
,
b
(
a
,
b
)
φ
b
,
c
(
b
,
c
)
φ
(
b
,
d
)
(
b
,
d
)
p ( a , b , c , d ) = \frac { 1 } { Z } \varphi _ { a } ( a ) \varphi _ { b } ( b ) \varphi _ { c } ( c ) \varphi _ { d } ( d ) \cdot \varphi _ { a , b } ( a , b ) \varphi _ { b , c } ( b , c ) \varphi ( b , d ) ( b , d )
p(a,b,c,d)=Z1φa(a)φb(b)φc(c)φd(d)⋅φa,b(a,b)φb,c(b,c)φ(b,d)(b,d) 我们要求
p
(
a
)
=
∑
b
,
c
,
d
p
(
a
,
b
,
c
,
d
)
p(a) =\sum_{b,c,d} p(a,b,c,d)
p(a)=∑b,c,dp(a,b,c,d)和
p
(
b
)
=
∑
a
,
c
,
d
p
(
a
,
b
,
c
,
d
)
p(b) =\sum_{a,c,d} p(a,b,c,d)
p(b)=∑a,c,dp(a,b,c,d),其间一定会出现大量的重复计算。这个模型中有四个点,三条边,每条边都有两个方向,所以我们要求的是6 个“积木”。我们来一步步 的看看,如何可以得到想要的
p
(
a
)
p(a)
p(a)。
首先,我们需要求的是
c
→
b
c \rightarrow b
c→b和
d
→
b
d \rightarrow b
d→b两个过程。其中,
c
→
b
c \rightarrow b
c→b的过程也就是
m
c
→
b
(
b
)
m _ {c \rightarrow b } ( b)
mc→b(b)可以被我们表达为
∑
c
φ
c
⋅
φ
b
,
c
\sum_{c} \varphi _ { c} \cdot \varphi _ { b,c}
∑cφc⋅φb,c。同理,
m
d
→
b
(
b
)
m _ {d \rightarrow b } ( b)
md→b(b)可以被我们表达为
∑
d
φ
b
⋅
φ
b
,
d
\sum_{d} \varphi _ { b} \cdot \varphi _ { b,d}
∑dφb⋅φb,d第二步,我们需要求
b
→
a
b \rightarrow a
b→a的过程,也就是
m
b
→
a
(
a
)
m _ {b\rightarrow a } ( a)
mb→a(a)。它等于
m
c
→
b
(
b
)
m _ {c \rightarrow b } ( b)
mc→b(b),
m
d
→
b
(
b
)
m _ {d \rightarrow b } ( b)
md→b(b)乘上
b
b
b己的部分求和得到,我们可以写为:
m
b
→
a
(
a
)
=
∑
b
m
c
→
b
(
b
)
⋅
φ
b
⋅
φ
a
,
b
⋅
m
d
→
b
(
b
)
m _ { b \rightarrow a } ( a ) = \sum _ { b } m _ { c \rightarrow b } ( b ) \cdot \varphi _ { b } \cdot \varphi _ { a , b } \cdot m _ { d \rightarrow b } ( b )
mb→a(a)=b∑mc→b(b)⋅φb⋅φa,b⋅md→b(b)最后,
m
b
→
a
(
a
)
m _ {b\rightarrow a } ( a)
mb→a(a)乘上a 自己的部分就得到了
p
(
a
)
p(a)
p(a),也就是:
p
(
a
)
=
φ
a
⋅
m
b
→
a
(
a
)
p(a) = φ_a \cdot m _ {b\rightarrow a } ( a)
p(a)=φa⋅mb→a(a)。 所以,我们总结一下:
m
b
→
a
(
x
a
)
=
∑
x
b
φ
a
,
b
φ
b
m
c
→
b
(
x
b
)
m
d
→
b
(
x
b
)
m _ { b \rightarrow a } ( x _ { a } ) = \sum _ { x _ { b } } \varphi _ { a , b } \varphi _ { b } m _ { c \rightarrow b } ( x _ { b } ) m _ { d \rightarrow b } ( x _ { b } )
mb→a(xa)=xb∑φa,bφbmc→b(xb)md→b(xb) 而
p
(
a
)
=
φ
a
⋅
m
b
→
a
(
a
)
p(a) = φ_a \cdot m _ {b\rightarrow a } ( a)
p(a)=φa⋅mb→a(a)。 我相信到这里,大家应该是可以理解这个意思的,会有点抽象,但并不是很难。下一步我想做个Generalize 为了便于大家进行理解,我这里尽量不跳步:
m
b
→
a
(
x
a
)
=
∑
x
b
φ
a
,
b
φ
b
∏
{
k
∈
N
B
(
b
)
}
−
a
m
k
→
b
(
x
b
)
m _ { b \rightarrow a } ( x _ { a } ) = \sum _ { x _ { b } } \varphi _ { a , b } \varphi _ { b } \prod _ { \{ k \in N B ( b ) \} - a } m _ { k \rightarrow b } ( x _ { b } )
mb→a(xa)=xb∑φa,bφb{k∈NB(b)}−a∏mk→b(xb) 这里的NB(b) 代表的是所有节点b 的邻接节点。我们可以进一步表示为:
m
j
→
i
(
x
i
)
=
∑
x
j
φ
i
,
j
φ
j
∏
{
k
∈
N
B
(
j
)
}
−
i
m
k
→
j
(
x
j
)
m _ { j \rightarrow i } ( x _ { i } ) = \sum _ { x _ { j } } \varphi _ { i , j } \varphi _ { j } \prod _ { \{ k \in N B ( j ) \} - i } m _ { k \rightarrow j} ( x _ { j } )
mj→i(xi)=xj∑φi,jφj{k∈NB(j)}−i∏mk→j(xj) 而
p
(
x
i
)
=
φ
i
∏
k
∈
N
B
(
i
)
m
k
→
i
(
x
i
)
p(x_i)= \varphi _ { i } \prod _ { k \in N B ( i) } m _ { k \rightarrow i} ( x _ { i } )
p(xi)=φik∈NB(i)∏mk→i(xi) 通过对上面表达式的观察,我们是不是发现了一个很有意思的现象。也就是这些概率都是由
m
i
→
j
m _ { i \rightarrow j}
mi→j这样的小积木拼接起来的。所以我们可以get a conclusion:我们不要一上来就直接去求边缘概率密度,比如
p
(
a
)
,
p
(
b
)
,
p
(
c
)
,
p
(
d
)
p(a), p(b), p(c),p(d)
p(a),p(b),p(c),p(d)这些的。我们可以先建立一个Cache,把
m
i
→
j
m _ { i \rightarrow j}
mi→j全部算出来。然后,要求什么的话,直接进行搭建和拼接就可以了。从这里,我们就引出了Belief Propagation。
3.2.1 Sequential Implementation
顺序计算的思路,我们需要借助一个队列来实现:
Get Root: 首先我们需要假设一个节点为根节点。Collect Message: 对于每一个在根节点的邻接点中的节点
x
i
x_i
xi,Collect Message (
x
i
x_i
xi)。对应的就是图2 中蓝色的线条。Distribute Message: 对于每一个在根节点的邻接点中的节点
x
i
x_i
xiDistribute Message (
x
i
x_i
xi)。对应的就是图2 中红色的线条。
经过这三个步骤以后,我们可以得到所有的
i
,
j
∈
v
i,j \in v
i,j∈v,从而计算出
p
(
x
k
)
,
k
∈
v
p(x_k), k \in v
p(xk),k∈v。
3.2.2 Parallel Implementation
这种思想在图结构的网络中经常使用,大致也就是随意选一个节点,然后向四周其他的节点辐射信息。其他节点收到信息之后,更新自己的状态,然后反馈自己的信息给源节点,源节点再更新自己的信息。不断地重复这个工作,直到最后收敛为止。
3.3 小结
实际上,Belief Propagation 就是一种Variable Elimination。但是,我们发现了Variable Elimination中有很多的重复计算。所以,我们想到了提取出来先算好,要用的时候直接放进去就行了。所以,Belief Propagation 中分解了传递的过程,先计算消息传递的机制,再来组装出计算边缘概率。其实本质还是Variable Elimination 算法,不过就是使表达更加的规范了,通过拆解的方法来消除重复计算。 BP算法的优点:
缓存
m
i
→
j
m _ { i \rightarrow j}
mi→j,减少重复计算,时间复杂度低计算
m
i
→
j
m _ { i \rightarrow j}
mi→j的过程中不想干的分支可以进行并行计算
4 Max Product Algorithm
我们在这里再总结一下概率图模型有什么用。对于一个图,Graph ={
X
,
E
X,E
X,E},其中
X
X
X 代表的是普通变量,
E
E
E 代表的是Evidence,也就是观测变量。
首先要解决的是边缘变量的问题,也就是已知:
E
=
E =
E={
e
1
,
e
2
,
⋯
,
e
k
e_1,e_2,\cdots,e_k
e1,e2,⋯,ek},如何求
p
(
E
)
p(E)
p(E)的问题,其中
E
E
E 为一个变量或者为一个子集。实际上就是一个likelihood 的问题。条件概率,也就是一个求后验概率的问题,目标概率为
X
=
(
Y
;
Z
)
X = (Y;Z)
X=(Y;Z)。而
p
(
Y
∣
E
)
=
∑
z
p
(
X
∣
E
)
p(Y |E) =\sum_z p(X|E)
p(Y∣E)=∑zp(X∣E)。最大后验估计(MAP),也被我们称为Decoding 的问题。也就是我们希望找到一个隐序列,使得:
x
^
=
a
r
g
m
a
x
x
p
(
X
∣
E
)
,
y
^
=
a
r
g
m
a
x
y
p
(
Y
∣
E
)
\hat{x} = argmax_x p(X|E),\hat{y} = argmax_y p(Y|E)
x^=argmaxxp(X∣E),y^=argmaxyp(Y∣E)。
这里的Max-Product 算法和隐马尔可夫模型(HMM) 中的Viterbi 算法非常的类似。其实,从算法上讲它就是Belief Propagation 算法的一种改进,从模型上讲是Viterbi 算法的推广。在这里我们求的不是概率值了,而是一个最优的概率序列
(
a
^
,
b
^
,
c
^
,
d
^
)
=
a
r
g
m
a
x
a
,
b
,
c
,
d
p
(
x
a
,
x
b
,
x
c
,
x
d
∣
E
)
(\hat{a},\hat{b},\hat{c},\hat{d})=\mathop{argmax}_{a,b,c,d}p(x_a,x_b,x_c,x_d|E)
(a^,b^,c^,d^)=argmaxa,b,c,dp(xa,xb,xc,xd∣E)
4.1 Max Product Algorithm
下面展示一个树的拓扑结构图。  在这个树中,我们将
m
b
→
a
m _ { b \rightarrow a}
mb→a看成是能使
p
(
x
a
,
x
b
,
x
c
,
x
d
∣
E
)
p(x_a,x_b,x_c,x_d|E)
p(xa,xb,xc,xd∣E) 联合概率达到最大的值。每一个节点代表的是到这个节点为止的路径联合概率达到最大的值。我们表达为:
m
j
→
i
=
max
x
j
ϕ
j
ϕ
i
j
∏
k
∈
N
e
i
g
h
b
o
u
r
(
j
)
−
i
m
k
→
j
m_{j\to i}=\max\limits_{x_j}\phi_j\phi_{ij}\prod\limits_{k\in Neighbour(j)-i}m_{k\to j}
mj→i=xjmaxϕjϕijk∈Neighbour(j)−i∏mk→j 那么,在图一所示的概率图模型中,
m
c
→
b
m_{c\to b}
mc→b 可以表示为:
m
c
→
b
=
max
x
c
φ
c
⋅
φ
b
c
m_{c\to b}=\max\limits_{x_c}\varphi_c \cdot \varphi_{bc}
mc→b=xcmaxφc⋅φbc 其中,
φ
c
⋅
φ
b
c
φ_c \cdot φ_{bc}
φc⋅φbc 可以表示为和
c
c
c 相关的函数。
m
d
→
b
=
max
x
d
φ
d
⋅
φ
b
d
m_{d\to b}=\max\limits_{x_d}\varphi_d \cdot \varphi_{bd}
md→b=xdmaxφd⋅φbd 其中,
φ
d
⋅
φ
b
d
φ_d \cdot φ_{bd}
φd⋅φbd 可以表示为和
d
d
d 相关的函数。
m
b
→
a
=
max
x
b
φ
b
⋅
φ
a
b
⋅
m
c
→
b
⋅
m
d
→
b
m_{b\to a}=\max_{x_b }\varphi_b \cdot \varphi_{ab}\cdot m_{c\to b} \cdot m_{d\to b}
mb→a=xbmaxφb⋅φab⋅mc→b⋅md→b 最终,我们将得到的是:
max
p
(
a
,
b
,
c
,
d
)
=
max
x
a
φ
a
⋅
m
b
→
a
\max p(a,b,c,d) =\max_{x_a} \varphi_{a}\cdot m_{b\to a}
maxp(a,b,c,d)=xamaxφa⋅mb→a 而
φ
a
⋅
m
b
→
a
\varphi_{a}\cdot m_{b\to a}
φa⋅mb→a 就可以看成是一个关于a 的函数。这里我们再提一下Belief Propagation,这里的Max-Product 实际上就是Belief Propagation 的一个变形。 在这个树中,我们将
m
b
→
a
m _ { b \rightarrow a}
mb→a看成是能使
p
(
x
a
,
x
b
,
x
c
,
x
d
∣
E
)
p(x_a,x_b,x_c,x_d|E)
p(xa,xb,xc,xd∣E) 联合概率达到最大的值。每一个节点代表的是到这个节点为止的路径联合概率达到最大的值。我们表达为:
m
j
→
i
=
max
x
j
ϕ
j
ϕ
i
j
∏
k
∈
N
e
i
g
h
b
o
u
r
(
j
)
−
i
m
k
→
j
m_{j\to i}=\max\limits_{x_j}\phi_j\phi_{ij}\prod\limits_{k\in Neighbour(j)-i}m_{k\to j}
mj→i=xjmaxϕjϕijk∈Neighbour(j)−i∏mk→j 那么,在图一所示的概率图模型中,
m
c
→
b
m_{c\to b}
mc→b 可以表示为:
m
c
→
b
=
max
x
c
φ
c
⋅
φ
b
c
m_{c\to b}=\max\limits_{x_c}\varphi_c \cdot \varphi_{bc}
mc→b=xcmaxφc⋅φbc 其中,
φ
c
⋅
φ
b
c
φ_c \cdot φ_{bc}
φc⋅φbc 可以表示为和
c
c
c 相关的函数。
m
d
→
b
=
max
x
d
φ
d
⋅
φ
b
d
m_{d\to b}=\max\limits_{x_d}\varphi_d \cdot \varphi_{bd}
md→b=xdmaxφd⋅φbd 其中,
φ
d
⋅
φ
b
d
φ_d \cdot φ_{bd}
φd⋅φbd 可以表示为和
d
d
d 相关的函数。
m
b
→
a
=
max
x
b
φ
b
⋅
φ
a
b
⋅
m
c
→
b
⋅
m
d
→
b
m_{b\to a}=\max_{x_b }\varphi_b \cdot \varphi_{ab}\cdot m_{c\to b} \cdot m_{d\to b}
mb→a=xbmaxφb⋅φab⋅mc→b⋅md→b 最终,我们将得到的是:
max
p
(
a
,
b
,
c
,
d
)
=
max
x
a
φ
a
⋅
m
b
→
a
\max p(a,b,c,d) =\max_{x_a} \varphi_{a}\cdot m_{b\to a}
maxp(a,b,c,d)=xamaxφa⋅mb→a 而
φ
a
⋅
m
b
→
a
\varphi_{a}\cdot m_{b\to a}
φa⋅mb→a 就可以看成是一个关于a 的函数。这里我们再提一下Belief Propagation,这里的Max-Product 实际上就是Belief Propagation 的一个变形。
4.2 Belief Propagation
实际上这个算法的提出时因为,多次求边缘概率密度会发现中间有很多的步骤是重复的。我们用
m
i
→
j
m_{i \to j}
mi→j 记录每一个边缘概率,最后进行组合就行。所以,
m
j
→
i
(
x
i
)
=
∑
x
j
φ
i
,
j
(
x
i
,
x
j
)
φ
j
(
x
j
)
∏
{
k
∈
N
B
(
j
)
}
−
i
m
k
→
j
(
x
j
)
\left. \begin{array} { c } { m _ { j \rightarrow i } ( x _ { i } ) = \sum _ { x _ { j } } \varphi _ { i , j } ( x _ { i } , x _ { j } ) \varphi _ { j } ( x _ { j } ) \prod _ { \{ k \in N B ( j ) \} -i } m _ { k \rightarrow j } ( x _ { j } ) } \end{array} \right.
mj→i(xi)=∑xjφi,j(xi,xj)φj(xj)∏{k∈NB(j)}−imk→j(xj)
p
(
x
i
)
=
φ
(
x
i
)
∏
k
∈
N
B
(
x
i
)
m
k
→
i
∣
(
x
i
)
\left. \begin{array} { c } { p ( x _ { i } ) = \varphi ( x _ { i } ) \prod _ { k \in N B ( x _ { i } ) } m _ { k \rightarrow i } | ( x _ { i } ) } \end{array} \right.
p(xi)=φ(xi)∏k∈NB(xi)mk→i∣(xi)
4.3 Compare
其实,我们一比较就可以很简单的看出,Max-product 和Belief Propagation 只有一个地方不一样。那就是前者是求最大,后者是求和。也就是Max-product 到Sum-product。在求得了
m
a
x
p
(
a
,
b
,
c
,
d
)
=
m
a
x
x
a
φ
a
m
b
→
a
max p(a, b, c, d) =max_{x_a} φ_a m_{b\to a}
maxp(a,b,c,d)=maxxaφamb→a 之后,我们利用回溯法我们比较就可以比较简单的得到
x
a
∗
,
x
b
∗
,
x
c
∗
,
x
d
∗
x_a^*,x_b^*,x_c^*,x_d^*
xa∗,xb∗,xc∗,xd∗了。在这个算法中,我们就不需要事先计算
m
i
→
j
m_{i\to j}
mi→j 了,直接在迭代中进行计算就可以了,也不会存在什么重复计算的问题。
|
 Hidden Markov Model (HMM) 算法将在后面的章节中做详细的描述,在这一小节中,我们主要做一点概述性的描述。HMM 的模型可视化为上图所示,其中O 是隐变量,也就是我们的观测变量。 我们主要考虑三个问题,在三个问题为Inference 的问题。1. Evaluation,也就是求一个边缘密度
p
(
O
)
=
∑
I
P
(
I
,
O
)
p(O)=\sum_{I} P(I, O)
p(O)=∑IP(I,O)。2. Learning,也就是寻找
λ
^
∘
\hat{\lambda}_{\circ}
λ^∘ 3. Decoding:
I
^
=
argmax
I
P
(
I
∣
O
)
\hat{I}=\operatorname{argmax}_{I} P(I | O)
I^=argmaxIP(I∣O),包括Vitebi Algorithm,这是一个动态规划算法。而隐马尔可夫模型实际上一种动态规划模型(Dynamic Bayesian Network)。
Hidden Markov Model (HMM) 算法将在后面的章节中做详细的描述,在这一小节中,我们主要做一点概述性的描述。HMM 的模型可视化为上图所示,其中O 是隐变量,也就是我们的观测变量。 我们主要考虑三个问题,在三个问题为Inference 的问题。1. Evaluation,也就是求一个边缘密度
p
(
O
)
=
∑
I
P
(
I
,
O
)
p(O)=\sum_{I} P(I, O)
p(O)=∑IP(I,O)。2. Learning,也就是寻找
λ
^
∘
\hat{\lambda}_{\circ}
λ^∘ 3. Decoding:
I
^
=
argmax
I
P
(
I
∣
O
)
\hat{I}=\operatorname{argmax}_{I} P(I | O)
I^=argmaxIP(I∣O),包括Vitebi Algorithm,这是一个动态规划算法。而隐马尔可夫模型实际上一种动态规划模型(Dynamic Bayesian Network)。 那么我们怎么来求
p
(
d
)
p(d)
p(d) 呢?根据公式我们可以得到:
p
(
d
)
=
∑
a
,
b
,
c
p
(
a
,
b
,
c
,
d
)
p(d)=\sum_{a,b,c}p(a,b,c,d)
p(d)=a,b,c∑p(a,b,c,d) 然后使用因子分解,我们可以得到:
p
(
d
)
=
∑
a
,
b
,
c
p
(
a
)
p
(
b
∣
a
)
p
(
c
∣
b
)
p
(
d
∣
c
)
p(d)=\sum_{a,b,c}p(a)p(b|a)p(c|b)p(d|c)
p(d)=a,b,c∑p(a)p(b∣a)p(c∣b)p(d∣c) 假定,
a
,
b
,
c
,
d
a,b,c,d
a,b,c,d 都为均匀离散的二值random variable,所以
a
,
b
,
c
,
d
∈
a,b,c,d\in
a,b,c,d∈ {0,1}。 所以,
p
(
d
)
=
p
(
a
=
0
)
⋅
p
(
b
=
0
∣
a
=
0
)
⋅
p
(
c
=
0
∣
b
=
0
)
⋅
p
(
d
∣
c
=
0
)
+
p
(
a
=
1
)
⋅
p
(
b
=
0
∣
a
=
1
)
⋅
p
(
c
=
0
∣
b
=
0
)
⋅
p
(
d
∣
c
=
0
)
+
⋯
+
p
(
a
=
1
)
⋅
p
(
b
=
1
∣
a
=
1
)
⋅
p
(
c
=
1
∣
b
=
1
)
⋅
p
(
d
∣
c
=
1
)
\begin{aligned} p(d) &=p(a = 0) \cdot p(b = 0|a = 0) \cdot p(c = 0|b = 0) \cdot p(d|c = 0) \\ & +p(a = 1) \cdot p(b = 0|a = 1) \cdot p(c = 0|b = 0) \cdot p(d|c = 0) \\ &+\cdots \\ &+p(a = 1) \cdot p(b = 1|a = 1) \cdot p(c = 1|b = 1) \cdot p(d|c = 1) \end{aligned}
p(d)=p(a=0)⋅p(b=0∣a=0)⋅p(c=0∣b=0)⋅p(d∣c=0)+p(a=1)⋅p(b=0∣a=1)⋅p(c=0∣b=0)⋅p(d∣c=0)+⋯+p(a=1)⋅p(b=1∣a=1)⋅p(c=1∣b=1)⋅p(d∣c=1) 实际上,这里有8 个因子的积。那么我们来做进一步的分析,我们可以令
p
(
d
)
=
∑
a
,
b
,
c
p
(
a
)
p
(
b
∣
a
)
p
(
c
∣
b
)
p
(
d
∣
c
)
=
∑
b
,
c
p
(
c
∣
b
)
p
(
d
∣
c
)
∑
a
p
(
a
)
p
(
b
∣
a
)
\begin{aligned} p(d) &=\sum_{a,b,c}p(a)p(b|a)p(c|b)p(d|c) \\ & =\sum_{b,c}p(c|b)p(d|c)\sum_{a}p(a)p(b|a) \end{aligned}
p(d)=a,b,c∑p(a)p(b∣a)p(c∣b)p(d∣c)=b,c∑p(c∣b)p(d∣c)a∑p(a)p(b∣a) 而
p
(
a
)
p
(
b
∣
a
)
=
p
(
a
,
b
)
p(a)p(b|a) = p(a,b)
p(a)p(b∣a)=p(a,b),而
∑
a
p
(
a
)
p
(
b
∣
a
)
=
p
(
b
)
\sum_a p(a)p(b|a) = p(b)
∑ap(a)p(b∣a)=p(b)。我们可以将
a
a
a 看成
ϕ
(
a
)
ϕ(a)
ϕ(a) 这是一个和
a
a
a 相关的函数,同理
p
(
b
∣
a
)
p(b|a)
p(b∣a)看成
ϕ
(
a
,
b
)
ϕ(a, b)
ϕ(a,b)。所以,我们可以将
∑
a
p
(
a
)
p
(
b
∣
a
)
\sum_a p(a)p(b|a)
∑ap(a)p(b∣a) 看成
ϕ
a
(
b
)
ϕ_a(b)
ϕa(b),这样就相当于一个关于
b
b
b 的函数,并且是从
a
a
a 中导出的。所以,我们做如下替换可得:
∑
b
,
c
p
(
c
∣
b
)
p
(
d
∣
c
)
∑
a
p
(
a
)
p
(
b
∣
a
)
=
∑
b
,
c
p
(
c
∣
b
)
p
(
d
∣
c
)
ϕ
a
b
=
∑
c
p
(
d
∣
c
)
∑
b
p
(
c
∣
b
)
ϕ
a
b
\sum_{b,c}p(c|b)p(d|c)\sum_{a}p(a)p(b|a)=\sum_{b,c}p(c|b)p(d|c)ϕ_{a}b=\sum_{c}p(d|c)\sum_{b}p(c|b)ϕ_{a}b
b,c∑p(c∣b)p(d∣c)a∑p(a)p(b∣a)=b,c∑p(c∣b)p(d∣c)ϕab=c∑p(d∣c)b∑p(c∣b)ϕab 同理,我们将
∑
b
p
(
c
∣
b
)
ϕ
a
b
\sum_{b}p(c|b)ϕ_{a}b
∑bp(c∣b)ϕab 看成
ϕ
b
(
c
)
ϕ_b(c)
ϕb(c)。所以,原始将被改写为:
∑
c
p
(
d
∣
c
)
ϕ
b
(
c
)
=
ϕ
b
(
c
)
\sum_{c}p(d|c)ϕ_b(c)=ϕ_b(c)
c∑p(d∣c)ϕb(c)=ϕb(c) 这个算法的核心就是乘法对加法的分配律。那我们怎么类比到乘法的分配律呢?首先先来简单的回顾一下乘法的分配律,也就是
a
c
+
a
b
=
a
(
b
+
c
)
ac+ab = a(b+c)
ac+ab=a(b+c)。那么我们仔细的来看看这个计算p(d) 的过程。这是不是就是一个不断的提取公因子,进行计算的过程?有没有觉得和分配律很像?先提取
a
a
a 的部分,计算
a
a
a 的部分,然后再依次的提取
b
b
b 的部分,
c
c
c 的部分,最后剩下的就是
d
d
d 的部分。那么,我们就可以把这么一长串的公式进行逐步化简了,这就是变量消元的思想。同样,在无向图中,我们也可以使用到马尔可夫网络中。
p
(
a
,
b
,
c
,
d
)
=
1
z
∏
i
=
1
k
ϕ
c
i
(
x
c
i
)
p ( a , b , c , d ) = \frac { 1 } { z } \prod _ { i = 1 } ^ { k } \phi _ { c _ { i } } ( x _ { c _ { i } } )
p(a,b,c,d)=z1i=1∏kϕci(xci) 写成因子分解的形式就是
p
(
x
)
=
∏
x
i
ϕ
i
(
x
i
)
p ( x ) = \prod _ { x _ { i } } \phi _ { i } ( x _ { i } )
p(x)=xi∏ϕi(xi) 这实际上就是分配律,一个变量一个变量的提取,然后进行分解计算。同时这种算法的缺点也非常的明显。 首先,就是重复计算的问题,无论计算那个变量的概率都要重复的计算一遍所有的概率。这个原因就会导致算法的计算难度非常的大。第二个就是计算次序的问题,我们举的例子还比较的简单,所以我们可以一眼就看出来,按
a
−
b
−
c
−
d
a - b - c - d
a−b−c−d 的次序开始算。但是,实际上,并没有这么容易就得到计算的次序,而且计算次序不一样会导致计算的难度有很大的区别。而有数学家已经证明了,确定最优的计算顺序,本身就是一个NP hard 的问题,非常难求解。
那么我们怎么来求
p
(
d
)
p(d)
p(d) 呢?根据公式我们可以得到:
p
(
d
)
=
∑
a
,
b
,
c
p
(
a
,
b
,
c
,
d
)
p(d)=\sum_{a,b,c}p(a,b,c,d)
p(d)=a,b,c∑p(a,b,c,d) 然后使用因子分解,我们可以得到:
p
(
d
)
=
∑
a
,
b
,
c
p
(
a
)
p
(
b
∣
a
)
p
(
c
∣
b
)
p
(
d
∣
c
)
p(d)=\sum_{a,b,c}p(a)p(b|a)p(c|b)p(d|c)
p(d)=a,b,c∑p(a)p(b∣a)p(c∣b)p(d∣c) 假定,
a
,
b
,
c
,
d
a,b,c,d
a,b,c,d 都为均匀离散的二值random variable,所以
a
,
b
,
c
,
d
∈
a,b,c,d\in
a,b,c,d∈ {0,1}。 所以,
p
(
d
)
=
p
(
a
=
0
)
⋅
p
(
b
=
0
∣
a
=
0
)
⋅
p
(
c
=
0
∣
b
=
0
)
⋅
p
(
d
∣
c
=
0
)
+
p
(
a
=
1
)
⋅
p
(
b
=
0
∣
a
=
1
)
⋅
p
(
c
=
0
∣
b
=
0
)
⋅
p
(
d
∣
c
=
0
)
+
⋯
+
p
(
a
=
1
)
⋅
p
(
b
=
1
∣
a
=
1
)
⋅
p
(
c
=
1
∣
b
=
1
)
⋅
p
(
d
∣
c
=
1
)
\begin{aligned} p(d) &=p(a = 0) \cdot p(b = 0|a = 0) \cdot p(c = 0|b = 0) \cdot p(d|c = 0) \\ & +p(a = 1) \cdot p(b = 0|a = 1) \cdot p(c = 0|b = 0) \cdot p(d|c = 0) \\ &+\cdots \\ &+p(a = 1) \cdot p(b = 1|a = 1) \cdot p(c = 1|b = 1) \cdot p(d|c = 1) \end{aligned}
p(d)=p(a=0)⋅p(b=0∣a=0)⋅p(c=0∣b=0)⋅p(d∣c=0)+p(a=1)⋅p(b=0∣a=1)⋅p(c=0∣b=0)⋅p(d∣c=0)+⋯+p(a=1)⋅p(b=1∣a=1)⋅p(c=1∣b=1)⋅p(d∣c=1) 实际上,这里有8 个因子的积。那么我们来做进一步的分析,我们可以令
p
(
d
)
=
∑
a
,
b
,
c
p
(
a
)
p
(
b
∣
a
)
p
(
c
∣
b
)
p
(
d
∣
c
)
=
∑
b
,
c
p
(
c
∣
b
)
p
(
d
∣
c
)
∑
a
p
(
a
)
p
(
b
∣
a
)
\begin{aligned} p(d) &=\sum_{a,b,c}p(a)p(b|a)p(c|b)p(d|c) \\ & =\sum_{b,c}p(c|b)p(d|c)\sum_{a}p(a)p(b|a) \end{aligned}
p(d)=a,b,c∑p(a)p(b∣a)p(c∣b)p(d∣c)=b,c∑p(c∣b)p(d∣c)a∑p(a)p(b∣a) 而
p
(
a
)
p
(
b
∣
a
)
=
p
(
a
,
b
)
p(a)p(b|a) = p(a,b)
p(a)p(b∣a)=p(a,b),而
∑
a
p
(
a
)
p
(
b
∣
a
)
=
p
(
b
)
\sum_a p(a)p(b|a) = p(b)
∑ap(a)p(b∣a)=p(b)。我们可以将
a
a
a 看成
ϕ
(
a
)
ϕ(a)
ϕ(a) 这是一个和
a
a
a 相关的函数,同理
p
(
b
∣
a
)
p(b|a)
p(b∣a)看成
ϕ
(
a
,
b
)
ϕ(a, b)
ϕ(a,b)。所以,我们可以将
∑
a
p
(
a
)
p
(
b
∣
a
)
\sum_a p(a)p(b|a)
∑ap(a)p(b∣a) 看成
ϕ
a
(
b
)
ϕ_a(b)
ϕa(b),这样就相当于一个关于
b
b
b 的函数,并且是从
a
a
a 中导出的。所以,我们做如下替换可得:
∑
b
,
c
p
(
c
∣
b
)
p
(
d
∣
c
)
∑
a
p
(
a
)
p
(
b
∣
a
)
=
∑
b
,
c
p
(
c
∣
b
)
p
(
d
∣
c
)
ϕ
a
b
=
∑
c
p
(
d
∣
c
)
∑
b
p
(
c
∣
b
)
ϕ
a
b
\sum_{b,c}p(c|b)p(d|c)\sum_{a}p(a)p(b|a)=\sum_{b,c}p(c|b)p(d|c)ϕ_{a}b=\sum_{c}p(d|c)\sum_{b}p(c|b)ϕ_{a}b
b,c∑p(c∣b)p(d∣c)a∑p(a)p(b∣a)=b,c∑p(c∣b)p(d∣c)ϕab=c∑p(d∣c)b∑p(c∣b)ϕab 同理,我们将
∑
b
p
(
c
∣
b
)
ϕ
a
b
\sum_{b}p(c|b)ϕ_{a}b
∑bp(c∣b)ϕab 看成
ϕ
b
(
c
)
ϕ_b(c)
ϕb(c)。所以,原始将被改写为:
∑
c
p
(
d
∣
c
)
ϕ
b
(
c
)
=
ϕ
b
(
c
)
\sum_{c}p(d|c)ϕ_b(c)=ϕ_b(c)
c∑p(d∣c)ϕb(c)=ϕb(c) 这个算法的核心就是乘法对加法的分配律。那我们怎么类比到乘法的分配律呢?首先先来简单的回顾一下乘法的分配律,也就是
a
c
+
a
b
=
a
(
b
+
c
)
ac+ab = a(b+c)
ac+ab=a(b+c)。那么我们仔细的来看看这个计算p(d) 的过程。这是不是就是一个不断的提取公因子,进行计算的过程?有没有觉得和分配律很像?先提取
a
a
a 的部分,计算
a
a
a 的部分,然后再依次的提取
b
b
b 的部分,
c
c
c 的部分,最后剩下的就是
d
d
d 的部分。那么,我们就可以把这么一长串的公式进行逐步化简了,这就是变量消元的思想。同样,在无向图中,我们也可以使用到马尔可夫网络中。
p
(
a
,
b
,
c
,
d
)
=
1
z
∏
i
=
1
k
ϕ
c
i
(
x
c
i
)
p ( a , b , c , d ) = \frac { 1 } { z } \prod _ { i = 1 } ^ { k } \phi _ { c _ { i } } ( x _ { c _ { i } } )
p(a,b,c,d)=z1i=1∏kϕci(xci) 写成因子分解的形式就是
p
(
x
)
=
∏
x
i
ϕ
i
(
x
i
)
p ( x ) = \prod _ { x _ { i } } \phi _ { i } ( x _ { i } )
p(x)=xi∏ϕi(xi) 这实际上就是分配律,一个变量一个变量的提取,然后进行分解计算。同时这种算法的缺点也非常的明显。 首先,就是重复计算的问题,无论计算那个变量的概率都要重复的计算一遍所有的概率。这个原因就会导致算法的计算难度非常的大。第二个就是计算次序的问题,我们举的例子还比较的简单,所以我们可以一眼就看出来,按
a
−
b
−
c
−
d
a - b - c - d
a−b−c−d 的次序开始算。但是,实际上,并没有这么容易就得到计算的次序,而且计算次序不一样会导致计算的难度有很大的区别。而有数学家已经证明了,确定最优的计算顺序,本身就是一个NP hard 的问题,非常难求解。 联合概率可以被我们表示为:
p
(
a
,
b
,
c
,
d
,
e
)
=
p
(
a
)
⋅
p
(
b
∣
a
)
⋅
p
(
c
∣
b
)
⋅
p
(
d
∣
c
)
⋅
p
(
e
∣
d
)
p(a, b, c, d, e) = p(a) \cdot p(b|a) \cdot p(c|b) \cdot p(d|c) \cdot p(e|d)
p(a,b,c,d,e)=p(a)⋅p(b∣a)⋅p(c∣b)⋅p(d∣c)⋅p(e∣d)。 如果,我们想要求的是
p
(
e
)
p(e)
p(e),那么:
p
(
e
)
=
∑
a
,
b
,
c
,
d
p
(
a
,
b
,
c
,
d
,
e
)
=
∑
a
p
(
e
∣
d
)
⋅
∑
c
p
(
d
∣
c
)
⋅
∑
b
p
(
c
∣
b
)
⋅
∑
a
p
(
b
∣
a
)
⋅
p
(
a
)
\left. \begin{array}{l}{ p ( e ) = \sum _ { a , b , c , d } p ( a , b , c , d , e ) }\\ \\{ = \sum _ { a } p ( e | d ) \cdot \sum _ { c } p ( d | c ) \cdot \sum _ { b } p ( c | b ) \cdot \sum _ { a } p ( b | a ) \cdot p ( a ) }\end{array} \right.
p(e)=∑a,b,c,dp(a,b,c,d,e)=∑ap(e∣d)⋅∑cp(d∣c)⋅∑bp(c∣b)⋅∑ap(b∣a)⋅p(a) 为了简化表达,这里我们需要定义一个很重要的符号。因为
∑
a
p
(
b
∣
a
)
⋅
p
(
a
)
\sum _ { a } p ( b | a ) \cdot p ( a )
∑ap(b∣a)⋅p(a),是一个关于b 的表达式,也就是相当于把a 给约掉了。所以我们可以把
∑
a
p
(
b
∣
a
)
⋅
p
(
a
)
\sum _ { a } p ( b | a ) \cdot p ( a )
∑ap(b∣a)⋅p(a)记为
m
a
→
b
(
b
)
m _ { a \rightarrow b } ( b )
ma→b(b)。同理,我们也可以将
∑
c
p
(
d
∣
c
)
⋅
∑
b
p
(
c
∣
b
)
⋅
m
a
→
b
(
b
)
\sum _ { c } p ( d | c ) \cdot \sum _ { b } p ( c | b ) \cdot m _ { a \rightarrow b } ( b )
∑cp(d∣c)⋅∑bp(c∣b)⋅ma→b(b)记为
m
b
→
c
(
c
)
m _ { b \rightarrow c } ( c )
mb→c(c)。那么为了求得p(e),我们依次的求解顺序为
m
a
→
b
(
b
)
m _ { a \rightarrow b } ( b )
ma→b(b),
m
b
→
c
(
c
)
m _ { b \rightarrow c } ( c )
mb→c(c),
m
c
→
d
(
d
)
m _ { c \rightarrow d } ( d )
mc→d(d)和
m
d
→
e
(
e
)
m _ { d \rightarrow e } ( e )
md→e(e)。也就相当于沿着这个链这个马氏链一直往前走,也就是前向算法(Forward Algorithm)。我们用公式表达即为:
联合概率可以被我们表示为:
p
(
a
,
b
,
c
,
d
,
e
)
=
p
(
a
)
⋅
p
(
b
∣
a
)
⋅
p
(
c
∣
b
)
⋅
p
(
d
∣
c
)
⋅
p
(
e
∣
d
)
p(a, b, c, d, e) = p(a) \cdot p(b|a) \cdot p(c|b) \cdot p(d|c) \cdot p(e|d)
p(a,b,c,d,e)=p(a)⋅p(b∣a)⋅p(c∣b)⋅p(d∣c)⋅p(e∣d)。 如果,我们想要求的是
p
(
e
)
p(e)
p(e),那么:
p
(
e
)
=
∑
a
,
b
,
c
,
d
p
(
a
,
b
,
c
,
d
,
e
)
=
∑
a
p
(
e
∣
d
)
⋅
∑
c
p
(
d
∣
c
)
⋅
∑
b
p
(
c
∣
b
)
⋅
∑
a
p
(
b
∣
a
)
⋅
p
(
a
)
\left. \begin{array}{l}{ p ( e ) = \sum _ { a , b , c , d } p ( a , b , c , d , e ) }\\ \\{ = \sum _ { a } p ( e | d ) \cdot \sum _ { c } p ( d | c ) \cdot \sum _ { b } p ( c | b ) \cdot \sum _ { a } p ( b | a ) \cdot p ( a ) }\end{array} \right.
p(e)=∑a,b,c,dp(a,b,c,d,e)=∑ap(e∣d)⋅∑cp(d∣c)⋅∑bp(c∣b)⋅∑ap(b∣a)⋅p(a) 为了简化表达,这里我们需要定义一个很重要的符号。因为
∑
a
p
(
b
∣
a
)
⋅
p
(
a
)
\sum _ { a } p ( b | a ) \cdot p ( a )
∑ap(b∣a)⋅p(a),是一个关于b 的表达式,也就是相当于把a 给约掉了。所以我们可以把
∑
a
p
(
b
∣
a
)
⋅
p
(
a
)
\sum _ { a } p ( b | a ) \cdot p ( a )
∑ap(b∣a)⋅p(a)记为
m
a
→
b
(
b
)
m _ { a \rightarrow b } ( b )
ma→b(b)。同理,我们也可以将
∑
c
p
(
d
∣
c
)
⋅
∑
b
p
(
c
∣
b
)
⋅
m
a
→
b
(
b
)
\sum _ { c } p ( d | c ) \cdot \sum _ { b } p ( c | b ) \cdot m _ { a \rightarrow b } ( b )
∑cp(d∣c)⋅∑bp(c∣b)⋅ma→b(b)记为
m
b
→
c
(
c
)
m _ { b \rightarrow c } ( c )
mb→c(c)。那么为了求得p(e),我们依次的求解顺序为
m
a
→
b
(
b
)
m _ { a \rightarrow b } ( b )
ma→b(b),
m
b
→
c
(
c
)
m _ { b \rightarrow c } ( c )
mb→c(c),
m
c
→
d
(
d
)
m _ { c \rightarrow d } ( d )
mc→d(d)和
m
d
→
e
(
e
)
m _ { d \rightarrow e } ( e )
md→e(e)。也就相当于沿着这个链这个马氏链一直往前走,也就是前向算法(Forward Algorithm)。我们用公式表达即为:  如果是要求
p
(
c
)
p(c)
p(c),那么我们的传递过程为
a
→
b
→
c
←
d
←
e
a \rightarrow b\rightarrow c \leftarrow d\leftarrow e
a→b→c←d←e。这里,我们就不能只用前向算法来解决了,需要用到Forward-Backward 算法来解决了。也就是同时使用Forward 和Backward的方法,那么我们来看看
p
(
c
)
p(c)
p(c)怎么求?
p
(
c
)
=
∑
a
,
b
,
d
,
e
p
(
a
,
b
,
c
,
d
,
e
)
=
(
∑
b
p
(
c
∣
b
)
∑
a
p
(
b
∣
a
)
p
(
a
)
)
⋅
(
∑
d
p
(
d
∣
c
)
∑
e
p
(
e
∣
d
)
)
\begin{aligned} p ( c ) &= \sum _ { a , b , d , e } p ( a , b , c , d , e ) \\ \\ &= ( \sum _ { b } p ( c | b ) \sum _ { a } p ( b | a ) p ( a ) ) \cdot ( \sum _ { d } p ( d | c ) \sum _ { e } p ( e | d ) ) \end{aligned}
p(c)=a,b,d,e∑p(a,b,c,d,e)=(b∑p(c∣b)a∑p(b∣a)p(a))⋅(d∑p(d∣c)e∑p(e∣d)) 对比上面的计算
p
(
e
)
p(e)
p(e) 的过程,我们就可以发现,
∑
b
p
(
c
∣
b
)
∑
a
p
(
b
∣
a
)
p
(
a
)
\sum_{b} p ( c | b ) \sum_{a} p ( b | a ) p ( a )
∑bp(c∣b)∑ap(b∣a)p(a)部分的计算也就是
m
b
→
c
(
c
)
m _ { b \rightarrow c } ( c )
mb→c(c)的计算是一模一样的。所以说,Variable Elimination 里面有大量的重复计算。Belief 的想法很简单,也就是将
m
i
→
j
(
j
)
m _ { i \rightarrow j } ( j )
mi→j(j),全部事先计算好,就像一个个积木一样,然后再用这个积木来搭建运算。那么也就是,我们事先将方向全部定义好,正向和反向的全部都求了再说。为了进一步探究Belief Background,我们需要讨论一些更加Generalize 的情况。也就是从
C
h
a
i
n
→
T
r
e
e
Chain \rightarrow Tree
Chain→Tree,有向
→
\rightarrow
→无项的情况。
如果是要求
p
(
c
)
p(c)
p(c),那么我们的传递过程为
a
→
b
→
c
←
d
←
e
a \rightarrow b\rightarrow c \leftarrow d\leftarrow e
a→b→c←d←e。这里,我们就不能只用前向算法来解决了,需要用到Forward-Backward 算法来解决了。也就是同时使用Forward 和Backward的方法,那么我们来看看
p
(
c
)
p(c)
p(c)怎么求?
p
(
c
)
=
∑
a
,
b
,
d
,
e
p
(
a
,
b
,
c
,
d
,
e
)
=
(
∑
b
p
(
c
∣
b
)
∑
a
p
(
b
∣
a
)
p
(
a
)
)
⋅
(
∑
d
p
(
d
∣
c
)
∑
e
p
(
e
∣
d
)
)
\begin{aligned} p ( c ) &= \sum _ { a , b , d , e } p ( a , b , c , d , e ) \\ \\ &= ( \sum _ { b } p ( c | b ) \sum _ { a } p ( b | a ) p ( a ) ) \cdot ( \sum _ { d } p ( d | c ) \sum _ { e } p ( e | d ) ) \end{aligned}
p(c)=a,b,d,e∑p(a,b,c,d,e)=(b∑p(c∣b)a∑p(b∣a)p(a))⋅(d∑p(d∣c)e∑p(e∣d)) 对比上面的计算
p
(
e
)
p(e)
p(e) 的过程,我们就可以发现,
∑
b
p
(
c
∣
b
)
∑
a
p
(
b
∣
a
)
p
(
a
)
\sum_{b} p ( c | b ) \sum_{a} p ( b | a ) p ( a )
∑bp(c∣b)∑ap(b∣a)p(a)部分的计算也就是
m
b
→
c
(
c
)
m _ { b \rightarrow c } ( c )
mb→c(c)的计算是一模一样的。所以说,Variable Elimination 里面有大量的重复计算。Belief 的想法很简单,也就是将
m
i
→
j
(
j
)
m _ { i \rightarrow j } ( j )
mi→j(j),全部事先计算好,就像一个个积木一样,然后再用这个积木来搭建运算。那么也就是,我们事先将方向全部定义好,正向和反向的全部都求了再说。为了进一步探究Belief Background,我们需要讨论一些更加Generalize 的情况。也就是从
C
h
a
i
n
→
T
r
e
e
Chain \rightarrow Tree
Chain→Tree,有向
→
\rightarrow
→无项的情况。 下面第一步,我们把上面那个模型的设置写出来。所以,我们需要进行因式分解,我们用
φ
(
i
)
φ(i)
φ(i)来表示和
i
i
i 有关的部分。所以,我们可以将联合概率密度写为:
p
(
a
,
b
,
c
,
d
)
=
1
Z
φ
a
(
a
)
φ
b
(
b
)
φ
c
(
c
)
φ
d
(
d
)
⋅
φ
a
,
b
(
a
,
b
)
φ
b
,
c
(
b
,
c
)
φ
(
b
,
d
)
(
b
,
d
)
p ( a , b , c , d ) = \frac { 1 } { Z } \varphi _ { a } ( a ) \varphi _ { b } ( b ) \varphi _ { c } ( c ) \varphi _ { d } ( d ) \cdot \varphi _ { a , b } ( a , b ) \varphi _ { b , c } ( b , c ) \varphi ( b , d ) ( b , d )
p(a,b,c,d)=Z1φa(a)φb(b)φc(c)φd(d)⋅φa,b(a,b)φb,c(b,c)φ(b,d)(b,d) 我们要求
p
(
a
)
=
∑
b
,
c
,
d
p
(
a
,
b
,
c
,
d
)
p(a) =\sum_{b,c,d} p(a,b,c,d)
p(a)=∑b,c,dp(a,b,c,d)和
p
(
b
)
=
∑
a
,
c
,
d
p
(
a
,
b
,
c
,
d
)
p(b) =\sum_{a,c,d} p(a,b,c,d)
p(b)=∑a,c,dp(a,b,c,d),其间一定会出现大量的重复计算。这个模型中有四个点,三条边,每条边都有两个方向,所以我们要求的是6 个“积木”。我们来一步步 的看看,如何可以得到想要的
p
(
a
)
p(a)
p(a)。
下面第一步,我们把上面那个模型的设置写出来。所以,我们需要进行因式分解,我们用
φ
(
i
)
φ(i)
φ(i)来表示和
i
i
i 有关的部分。所以,我们可以将联合概率密度写为:
p
(
a
,
b
,
c
,
d
)
=
1
Z
φ
a
(
a
)
φ
b
(
b
)
φ
c
(
c
)
φ
d
(
d
)
⋅
φ
a
,
b
(
a
,
b
)
φ
b
,
c
(
b
,
c
)
φ
(
b
,
d
)
(
b
,
d
)
p ( a , b , c , d ) = \frac { 1 } { Z } \varphi _ { a } ( a ) \varphi _ { b } ( b ) \varphi _ { c } ( c ) \varphi _ { d } ( d ) \cdot \varphi _ { a , b } ( a , b ) \varphi _ { b , c } ( b , c ) \varphi ( b , d ) ( b , d )
p(a,b,c,d)=Z1φa(a)φb(b)φc(c)φd(d)⋅φa,b(a,b)φb,c(b,c)φ(b,d)(b,d) 我们要求
p
(
a
)
=
∑
b
,
c
,
d
p
(
a
,
b
,
c
,
d
)
p(a) =\sum_{b,c,d} p(a,b,c,d)
p(a)=∑b,c,dp(a,b,c,d)和
p
(
b
)
=
∑
a
,
c
,
d
p
(
a
,
b
,
c
,
d
)
p(b) =\sum_{a,c,d} p(a,b,c,d)
p(b)=∑a,c,dp(a,b,c,d),其间一定会出现大量的重复计算。这个模型中有四个点,三条边,每条边都有两个方向,所以我们要求的是6 个“积木”。我们来一步步 的看看,如何可以得到想要的
p
(
a
)
p(a)
p(a)。 在这个树中,我们将
m
b
→
a
m _ { b \rightarrow a}
mb→a看成是能使
p
(
x
a
,
x
b
,
x
c
,
x
d
∣
E
)
p(x_a,x_b,x_c,x_d|E)
p(xa,xb,xc,xd∣E) 联合概率达到最大的值。每一个节点代表的是到这个节点为止的路径联合概率达到最大的值。我们表达为:
m
j
→
i
=
max
x
j
ϕ
j
ϕ
i
j
∏
k
∈
N
e
i
g
h
b
o
u
r
(
j
)
−
i
m
k
→
j
m_{j\to i}=\max\limits_{x_j}\phi_j\phi_{ij}\prod\limits_{k\in Neighbour(j)-i}m_{k\to j}
mj→i=xjmaxϕjϕijk∈Neighbour(j)−i∏mk→j 那么,在图一所示的概率图模型中,
m
c
→
b
m_{c\to b}
mc→b 可以表示为:
m
c
→
b
=
max
x
c
φ
c
⋅
φ
b
c
m_{c\to b}=\max\limits_{x_c}\varphi_c \cdot \varphi_{bc}
mc→b=xcmaxφc⋅φbc 其中,
φ
c
⋅
φ
b
c
φ_c \cdot φ_{bc}
φc⋅φbc 可以表示为和
c
c
c 相关的函数。
m
d
→
b
=
max
x
d
φ
d
⋅
φ
b
d
m_{d\to b}=\max\limits_{x_d}\varphi_d \cdot \varphi_{bd}
md→b=xdmaxφd⋅φbd 其中,
φ
d
⋅
φ
b
d
φ_d \cdot φ_{bd}
φd⋅φbd 可以表示为和
d
d
d 相关的函数。
m
b
→
a
=
max
x
b
φ
b
⋅
φ
a
b
⋅
m
c
→
b
⋅
m
d
→
b
m_{b\to a}=\max_{x_b }\varphi_b \cdot \varphi_{ab}\cdot m_{c\to b} \cdot m_{d\to b}
mb→a=xbmaxφb⋅φab⋅mc→b⋅md→b 最终,我们将得到的是:
max
p
(
a
,
b
,
c
,
d
)
=
max
x
a
φ
a
⋅
m
b
→
a
\max p(a,b,c,d) =\max_{x_a} \varphi_{a}\cdot m_{b\to a}
maxp(a,b,c,d)=xamaxφa⋅mb→a 而
φ
a
⋅
m
b
→
a
\varphi_{a}\cdot m_{b\to a}
φa⋅mb→a 就可以看成是一个关于a 的函数。这里我们再提一下Belief Propagation,这里的Max-Product 实际上就是Belief Propagation 的一个变形。
在这个树中,我们将
m
b
→
a
m _ { b \rightarrow a}
mb→a看成是能使
p
(
x
a
,
x
b
,
x
c
,
x
d
∣
E
)
p(x_a,x_b,x_c,x_d|E)
p(xa,xb,xc,xd∣E) 联合概率达到最大的值。每一个节点代表的是到这个节点为止的路径联合概率达到最大的值。我们表达为:
m
j
→
i
=
max
x
j
ϕ
j
ϕ
i
j
∏
k
∈
N
e
i
g
h
b
o
u
r
(
j
)
−
i
m
k
→
j
m_{j\to i}=\max\limits_{x_j}\phi_j\phi_{ij}\prod\limits_{k\in Neighbour(j)-i}m_{k\to j}
mj→i=xjmaxϕjϕijk∈Neighbour(j)−i∏mk→j 那么,在图一所示的概率图模型中,
m
c
→
b
m_{c\to b}
mc→b 可以表示为:
m
c
→
b
=
max
x
c
φ
c
⋅
φ
b
c
m_{c\to b}=\max\limits_{x_c}\varphi_c \cdot \varphi_{bc}
mc→b=xcmaxφc⋅φbc 其中,
φ
c
⋅
φ
b
c
φ_c \cdot φ_{bc}
φc⋅φbc 可以表示为和
c
c
c 相关的函数。
m
d
→
b
=
max
x
d
φ
d
⋅
φ
b
d
m_{d\to b}=\max\limits_{x_d}\varphi_d \cdot \varphi_{bd}
md→b=xdmaxφd⋅φbd 其中,
φ
d
⋅
φ
b
d
φ_d \cdot φ_{bd}
φd⋅φbd 可以表示为和
d
d
d 相关的函数。
m
b
→
a
=
max
x
b
φ
b
⋅
φ
a
b
⋅
m
c
→
b
⋅
m
d
→
b
m_{b\to a}=\max_{x_b }\varphi_b \cdot \varphi_{ab}\cdot m_{c\to b} \cdot m_{d\to b}
mb→a=xbmaxφb⋅φab⋅mc→b⋅md→b 最终,我们将得到的是:
max
p
(
a
,
b
,
c
,
d
)
=
max
x
a
φ
a
⋅
m
b
→
a
\max p(a,b,c,d) =\max_{x_a} \varphi_{a}\cdot m_{b\to a}
maxp(a,b,c,d)=xamaxφa⋅mb→a 而
φ
a
⋅
m
b
→
a
\varphi_{a}\cdot m_{b\to a}
φa⋅mb→a 就可以看成是一个关于a 的函数。这里我们再提一下Belief Propagation,这里的Max-Product 实际上就是Belief Propagation 的一个变形。