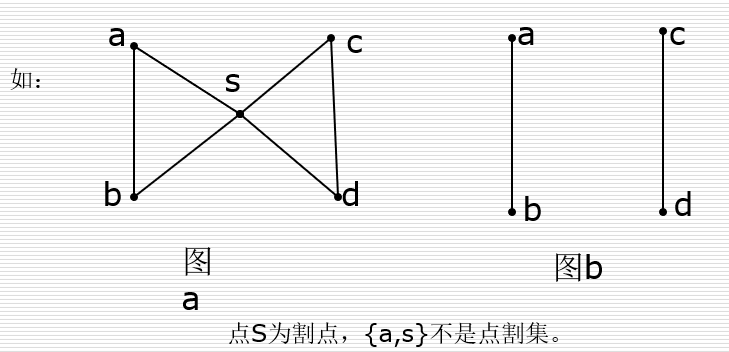
| 离散数学之图论复习笔记 | 您所在的位置:网站首页 › 数学笔记记什么 › 离散数学之图论复习笔记 |
离散数学之图论复习笔记
|
图论
7.1 图的基本概念
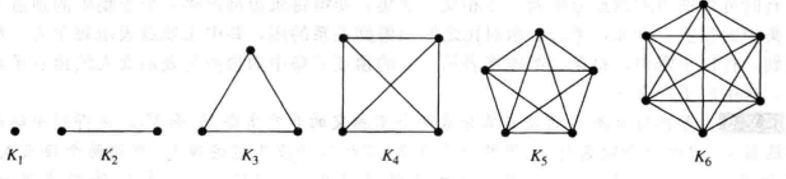
图的定义 一个图G是一个序偶〈V(G),E(G)〉,记为G=〈V(G),E(G)〉。其中V(G)是非空结点集合,E(G)是边集合,对E(G)中的每条边,有V(G)中的结点的有序偶或无序偶与之对应。 图G的结点与边之间的关系 邻接点:同一条边的两个端点。孤立点:没有边与之关联的结点。邻接边:关联同一个结点的两条边。孤立边:不与任何边相邻接的边。自回路(环):关联同一个结点的一条边((v,v)或)。平行边(多重边):关联同一对结点的多条边。图的分类 按G的结点个数和边数分为**(n,m)图**,即n个结点,m条边的图; 特别地,(n,0)称为零图,(1,0)图称为平凡图。 按G中关联于同一对结点的边数分为多重图和简单图; 多重图:含有平行边的图. 简单图:不含平行边和自环的图。 按G的边有序、无序分为有向图、无向图和混合图; 有向图:每条边都是有向边的图称为有向图; 无向图:每条边都是无向边的图称为无向图; 混合图:既有无向边,又有有向边的图称为混合图。 按G的边旁有无数量特征分为边权图、无权图; 按G的任意两个结点间是否有边分为完全图Kn 完全图:n个顶点的完全图记作K。是在每对不同顶点之间都恰有一条边的简单图。n ( n − 1 ) 2 \frac{n(n-1)}{2} 2n(n−1)
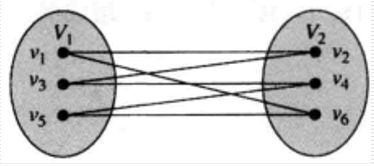
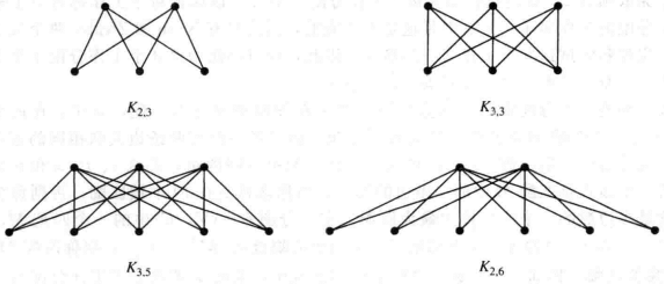
通俗理解:可以分为两个集合,两个集合中的每个点互不直接相连
通俗理解:在二分图的基础上,每个结点都连接另一个集合
 。零图和完全图互为补图
图的结点的度数及其计算
度数:图中结点v所关联的边数(有自回路时计算两次),记为deg(v) 。零图和完全图互为补图
图的结点的度数及其计算
度数:图中结点v所关联的边数(有自回路时计算两次),记为deg(v)
定理7.1.1:图G=中结点度数的总和等于边数的两倍,即: ∑ d e v ( v ) = 2 ∣ E ∣ \sum{dev(v)}=2|E| ∑dev(v)=2∣E∣ 证明:因为每条边都与两个结点关联,所以加上一条边就使得各结点度数的和增加2。 推论:图G中度数为奇数的结点必为偶数个。 有向图中 入度:射入结点v的边数称为结点v的入度,记为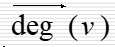 出度:由结点v射出的边数称为结点v的出度,记为 出度:由结点v射出的边数称为结点v的出度,记为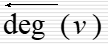 度数:结点v的入度+出度 度数:结点v的入度+出度
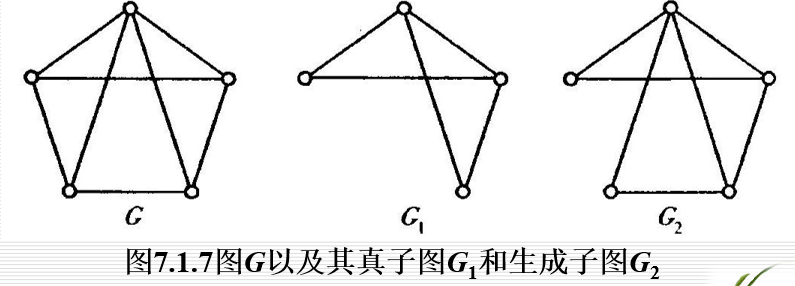
定理7.1.2:在任何有向图G=中,有 ∑ d e g ( v ) → = ∑ d e g ( v ) ← = ∣ E ∣ \sum{\overrightarrow{deg(v)}}=\sum{\overleftarrow{deg(v)}}=|E| ∑deg(v) =∑deg(v) =∣E∣ 子图:设有图G=和图G′=。 若 V ′ ⊆ V V'\subseteq V V′⊆V, E ′ ⊆ E E'\subseteq E E′⊆E,则称G′ 是G的子图。若G′是G的子图,且 E ′ ≠ E E'≠E E′=E,则称G′是G的真子图。若 V ′ = V , V'= V, V′=V, E ′ ⊆ E E' \subseteq E E′⊆E,则称G′是G的生成子图。
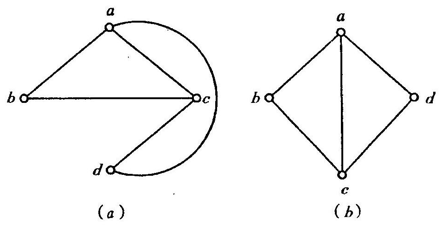 定义:设有图G=和图G′=。如果存在双射g:V→V′,使得e=(u,v)∈E, e′=(g(u),g(v))∈E′,且(u,v)与(g(u),g(v))有相同的重数,则称G与G′同构。记作G≌G′。
7.2 路与回路
路与回路
定义:设有图G=和图G′=。如果存在双射g:V→V′,使得e=(u,v)∈E, e′=(g(u),g(v))∈E′,且(u,v)与(g(u),g(v))有相同的重数,则称G与G′同构。记作G≌G′。
7.2 路与回路
路与回路
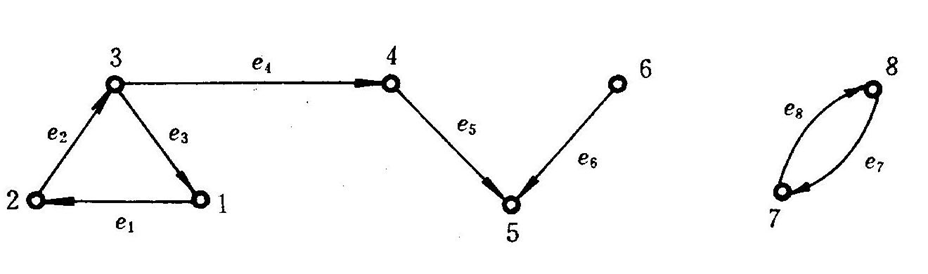
路:给定图G=,设v0,v1,…,vk∈V,e1,e2,…,ek∈E,其中ei是关联于结点vi-1和vi的边,称交替序列v0e1v1e2…ekvk为连接v0到vk的路,v0和vk分别称为路的起点与终点。 路的长度:路中边的数目k称作路的长度 回路:当v0=vk时,这条路称为回路 简单图:一条路v0e1v1e2…ekvk,可以表示为v0v1…vk 设μ=*v0*e1*v1*e2…ekvk是图G中连接v0到vk的路 迹:若e1,e2,…,ek都不相同,则称路μ为迹。 通路:若*v0,*v1,…,vk都不相同,则称路μ为通路。 图:长度大于2的闭的通路(即除v0=vk外,其余结点均不相同的路)μ称作圈 距离:在图G中,若结点vi到vj有路连接(这时称vi和vj是连通的),其中长度最短的路的长度称为vi到vj的距离,用符号d(vi,vj)表示。若从vi到vj不存在路径,则d(vi,vj)=∞。 图的连通性 无向图的连通性 在无向图如果一个图的任何两个结点之间都有一条路,那么我们称这个图是连通的,否则是不连通的。图G的一个连通的子图G′(称为连通子图)若不包含在G的任何更大的连通子图中,它就被称作G的连通分支。我们把图G的连通分支数记作W(G)。 有向图的连通性 在有向图中,如果若从结点u到v有一条路,则称u可达v。设有有向图图G 若G的任意两个结点中,至少从一个结点可达另一个结点,则称图G是单向连通的;如果G的任意两个结点都是相互可达的,则称图G是强连通的;如果略去边的方向后,G成为连通的无向图,则称图G是弱连通的。 强联通 > 单向联通 > 弱连通一个有向图G是强联通的,当且仅当G中有一个(有向)回路,它至少包含每个结点一次。在有向图G=〈V,E〉中,G′是G的子图,若G′是强连通的(单向连通的,弱连通的),没有包含G′的更大子图G″是强连通的(单向连通的,弱连通的),则称G′是G的强分图(单向分图,弱分图)。例子: 在下图中, 强分图集合是:{{1,2,3}, {4}, {5}, {6},{7,8}} 单向分图集合是:{{1,2,3,4,5},{6,5},{7,8}} 弱分图集合是:{{1,2,3,4,5,6}, {7,8}}
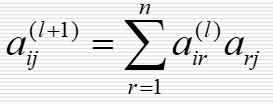 arj是联结vr和vj的长度为1的路数目a(l)ij是联结vi和vj的长度为l的路数目
可达性矩阵
设G=〈V,E〉是一个有n个结点的有向图,则n阶方阵P=(pij)称为图G的可达性矩阵
7.4 欧拉图与汉密尔顿图
欧拉图 arj是联结vr和vj的长度为1的路数目a(l)ij是联结vi和vj的长度为l的路数目
可达性矩阵
设G=〈V,E〉是一个有n个结点的有向图,则n阶方阵P=(pij)称为图G的可达性矩阵
7.4 欧拉图与汉密尔顿图
欧拉图
给定无孤立结点的图G,若存在一条经过G中每边一次且仅一次的回路,则该回路为欧拉回路。具有欧拉回路的图称为欧拉图。 充要条件:G的所有结点的度数都是偶数。 欧拉路:通过图G的每条边一次且仅一次的路称为图G的欧拉路 半欧拉图:有欧拉通路,无欧拉回路。 推论:一个多重连通图G有欧道路的充要条件是G中有且仅有有两个奇点。(从一个奇点到另一个奇点) 寻找欧拉回路:可以通过寻找回路,找公共顶点寻找 汉密尔顿图周游世界问题:能否找到一条旅行路线,使得沿着该旅行路线经过每座城市恰好一次,再回到原来的出发地呢? 汉密尔顿图:给定图G,若有一条路通过G中每个结点恰好一次,则这样的路称为汉密尔顿路;若有一个圈,通过G个每个结点恰好一次,这样的圈称为汉密尔顿回路(或汉密尔顿圈)。具有汉密尔顿回路的图称为汉密尔顿图。 必要条件:设图G=〈V,E〉是汉密尔顿图,则对于V的每个非空子集S,均有 W ( G - S ) ≤ ∣ S ∣ W(G-S)≤|S| W(G-S)≤∣S∣成立,其中W(G-S)是图G-S的连通分支数。 充分条件:图中任意不同两点的度数之和大于等于n。 平面图平面图:如果能把一个无向图G的所有结点和边画在平面上,使得任何两边除公共结点外没有其他交叉点,则称G为平面图,否则称G为非平面图。 面:设G是一个平面图,由图中的边所包围的其内部不包含图的结点和边的区域,称为G的一个面。 边界:包围该面的诸边所构成的回路称为这个面的边界。 度:面r的边界的长度(边数)称为该面的度,记为D®。 有限面:区域面积有限的面;无限面:区域面积无限的面 平面图有且仅有一个无限面 在一个平面图中,所有面度之和等于图中边数的二倍 欧拉公式Euler公式:设G为n结点m条边r个面的连通平面图,则n-m+r=2。 对于简单极大平面图,3n=2m(每个面由3条边组成,一边被2个面共享),代入得m=3n-6 对于具有k个连通分支的平面图G,有n-m+f=k+1 着色法 设G是某平面图的某个平面嵌入,构造G的对偶图 G如下: 在G的面R中放置G的顶点若G中的边e在G的面R与R的公共边界上,做G的边e与e相交,即e=(vi,vi),且e*不与其它任何边相交; |
【本文地址】