| 数学建模【微分方程模型(介绍、分析方法、数值模拟、传染病问题的建模和分析、经济增长模型、人口增长预测和控制模型)】 | 您所在的位置:网站首页 › 数学模型软件有哪些 › 数学建模【微分方程模型(介绍、分析方法、数值模拟、传染病问题的建模和分析、经济增长模型、人口增长预测和控制模型)】 |
数学建模【微分方程模型(介绍、分析方法、数值模拟、传染病问题的建模和分析、经济增长模型、人口增长预测和控制模型)】
|
🚀【MOOC数学建模与实验---学习笔记---整理汇总表】🚀 🌈【学习网址:MOOC---郑州轻工业大学---数学建模与实验】🌈 【第1、2章】【概述、软件介绍】【第3章】【数据处理方法】【第4章】【规划模型】【第5章】【图与网络模型】【第6章】【微分方程模型】【第7章】【统计模型】【第8章】【系统评价决策模型】【各个章节---作业题解析】目 录 6.1 微分方程模型介绍 微分方程模型介绍 一、建立微分方程 二、微分方程的解法 二,微分方程的解法之解析方法 二,微分方程的解法之数值方法 Matlab软件计算数值解 6.2 微分方程模型的分析方法 微分方程的解法 非线性微分方程的线性化 数值分析方法 6.3 微分方程模型的数值模拟 考虑Lorenz模型 地中海鲨鱼问题 食饵—捕食系统的数学模型 6.4 传染病问题的建模和分析 模型1 已感染人数i(t) 模型2 SI模型 模型3 SIS模型 模型4 SIR模型 6.5 经济增长模型 道格拉斯(Douglas)生产函数 资金与劳动力的最佳分配(静态模型) 经济(生产率)增长的条件(动态模型) Bernoulli方程 6.6 人口增长预测和控制模型 1、人口发展方程 2、连续型人口发展模型 3、模型求解 4、讨论 人口发展方程和生育率 人口指数---常用函数 6.1 微分方程模型介绍 微分方程模型介绍微分方程在现代科学的每一个领域都有广泛的应用,比如力学、运动学、电学、经济学、生物学、自动控制、化学等等,都可以看到大量利用微分方程表示的事物变化规律,这也体现了微分方程的重要性。 在高等数学中我们对微分方程有一定的认识,比如怎样求解一些简单的微分方程,对于一些细心的同学,可能想到对于复杂的微分方程的求解是一个重要的问题,但是,可能忽略一个同样重要的问题,那就是如何建立微分方程。同样是方程,其建立的过程一定程度上和前一部分方程的建立有相似之处,但不同之处是微分方程的建立过程中一般会涉及到变化率的概念(往往和时间有关)。比如运动学中速度是位移对时间的变化率,加速度是速度的变化率,电学中电流是电量的变化率,人口学中人口增长率是人口数对时间的 变化率等等。 分离变量法:求解微分方程(涉及时间变化) 化学反应、打气运动、人口数量变化、传染病发展规律 常微分方程、偏微分方程 滞后现象 差分方程 离散化,例:时间->一个单位一个单位地变化、天、年... 相邻不同节点之间的迭代关系 一、建立微分方程下面用一些常见的问题说明微分方程建模的基本方法。 例子1:放射性物质的衰变。 物理学家发现,放射性物质衰变的速度和物质的量成正比。 例子2:人口(生物数量)增长问题。 鱼类🐟、微生物、两种群之间的数量变化关系、人口数量(迁入、迁出) 通过观察发现,人口增长和现有人口数量成正比。 例子3:热传导问题。 牛顿定理表述热传导为:高温物体热量的散失速度和温度差成比例。 例子4:物体的运动问题。 物体运动可以用牛顿三大定律描述。 例子5:万有引力定理。 开普勒发现地球沿着以太阳为焦点的椭圆轨道运动,运动速度满足单位时间所扫过的面积相等。 例子6:传染病问题。 医学经验表明,传染病有几个关键要素,易感人群、带病人群,而传染往往通过两种人群的接触导致,不仅和易感人群和带病人群有关,还有他们 的接触有关。 例子7:战争问题。 交战双方的伤亡虽然比较复杂,但是大致遵循这样一些规律,比如武器的杀伤力、防御力,还有双方的人数对比等因素。 二、微分方程的解法解析方法 对于一些比较简单的微分方程,可以通过一些数学技巧解出,比如高等数学上接触的一些方程:可分离变量的方程、齐次方程、一阶线性微分方程、一些特殊的二阶常系数微分方程等等。 数值方法 能得到解析解的微分方程毕竟只是少数,对于从实际问题中提取的大量微分方程,无法得到方程的解析解,数值方法可以说是实际问题中必不可少的手段。 常见微分方程模型
关于微分方程的解,就是满足方程的一个函数族(或者一条曲线族)。我们又称其为微分方程的通解。用得更加广泛的是满足特定条 件的解,我们称其为特解。比如
c1... 微分方程的初始值 var1:微分方程涉及的变量
没有初始条件,求出的解 一般是 通解(Dy)。 指定变量为x,求出的方程 自变量为x,否则为t。
对于大量的微分方程,只能得到其数值解,一般而言,得到的解是方程的一个特解的近似。求微分方程数值解的方法很多,比如:欧拉法、龙格—库塔法等。其基本思想就是通过已知点得到函数值,并用该函数值代替一个小区间上函数的导数,得到在该区间上的一条直线,并用该直线作为方程特解的近似。有兴趣的同学可以参考微分方程数值解方面的著作。 Matlab软件计算数值解
solver 求解器 常用: ode23(运算速度快)、ode45(精度高)最常用。 ode15s(针对 刚性问题) 'f' 或者 @f 范例
范例
实际问题简化 --> 微分方程 非线性微分方程的线性化
观察结果 1、该曲线包含两个“圆盘”,每一个都是由螺线形轨道构成。某些轨道几乎是垂直地离开圆盘中一个而进入另一个。 2、随着t的增加,x(t)先绕一个圆盘几圈,然后“跳”到另一个圆盘中。绕第二个圆盘几圈,又跳回原来的圆盘。并以这样的方式继续 下去,在每个圆盘上绕的圈数是随机的。 思考:该空间曲线与初始点x0的选择有关吗?
1)x0=[0 0.1 0.1]‘;[t0,tf]=[0,30];解向量y 2)x00=[0.01 0.11 0.11]‘;[t0,tf]=[0,30];解向量x y – x = (y1-x1,y2-x2,y3-x3)。 注:这是这两个向量必须是同维数, 并且所取的时间节点应该相同。解决的办法是将[t0,tf]直接定义为如下的形式,比如0:0.1:30。 地中海鲨鱼问题
想:战争为什么使鲨鱼数量增加?是什么原因? 因为战争使捕鱼量下降,食用鱼增加,显然鲨鱼也随之增加。 但为何鲨鱼的比例大幅增加呢?生物学家Ancona无法解释这个现象,于是求助于著名的意大利数学家V.Volterra,希望建立一个食饵—捕食系统的数学模型,定量地回答这个问题。 食饵—捕食系统的数学模型
该模型反映了在没有人工捕获的自然环境中食饵与捕食者之间的制约关系,没有考虑食饵和捕食者自身的阻滞作用,是Volterra提出的最简单的模型。 给定一组具体数据,用matlab软件求解。 食饵 : 捕食(鲨鱼):
编制程序如下: % 1、建立m-文件shier.m如下: function dx=shier(t,x) dx=zeros(2,1); dx(1)=x(1)*(1-0.1*x(2)); dx(2)=x(2)*(-0.5+0.02*x(1)); % 2、建立主程序shark.m如下: [t,x]=ode45('shier',[0 15],[25 2]); plot(t,x(:,1),'-',t,x(:,2),'*') figure; plot(x(:,1),x(:,2))
初始条件:0时刻,i(0) =
di/dt:单位时间内,被感染者的变化率。 模型3 SIS模型
|
【本文地址】

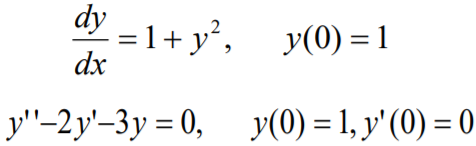
 eqn1:微分方程的第一个方程,... 微分方程表达式
eqn1:微分方程的第一个方程,... 微分方程表达式



 求特定解
求特定解





 混沌现象
混沌现象
 常见微分方程形式
常见微分方程形式 研究平衡点稳定性 -> 转化微分方程
研究平衡点稳定性 -> 转化微分方程
 系数矩阵 、雅可比矩阵
系数矩阵 、雅可比矩阵 需要写出 系数矩阵。
需要写出 系数矩阵。





 无解析表达式!!!
无解析表达式!!! 图像:周期变换
图像:周期变换
 考虑模型变化规律 洛伦兹系统---混沌系统
考虑模型变化规律 洛伦兹系统---混沌系统








 图2:周期变化
图2:周期变化 数量增加:滞后
数量增加:滞后 重心坐标的计算:高等数学...
重心坐标的计算:高等数学... i(t):在t时刻,被感染人数所占百分比
i(t):在t时刻,被感染人数所占百分比
 i随时间t的变化规律
i随时间t的变化规律 减小λ值,延迟高峰期的到来。
减小λ值,延迟高峰期的到来。


 降低 日接触率:隔离措施↑
降低 日接触率:隔离措施↑ 降低
降低 Q(t):以劳动力、资金为自变量的函数
Q(t):以劳动力、资金为自变量的函数 含义:二阶导数
含义:二阶导数