【高等数学笔记】二元函数连续、可微、偏导数存在、偏导数连续、任意方向导数存在的关系

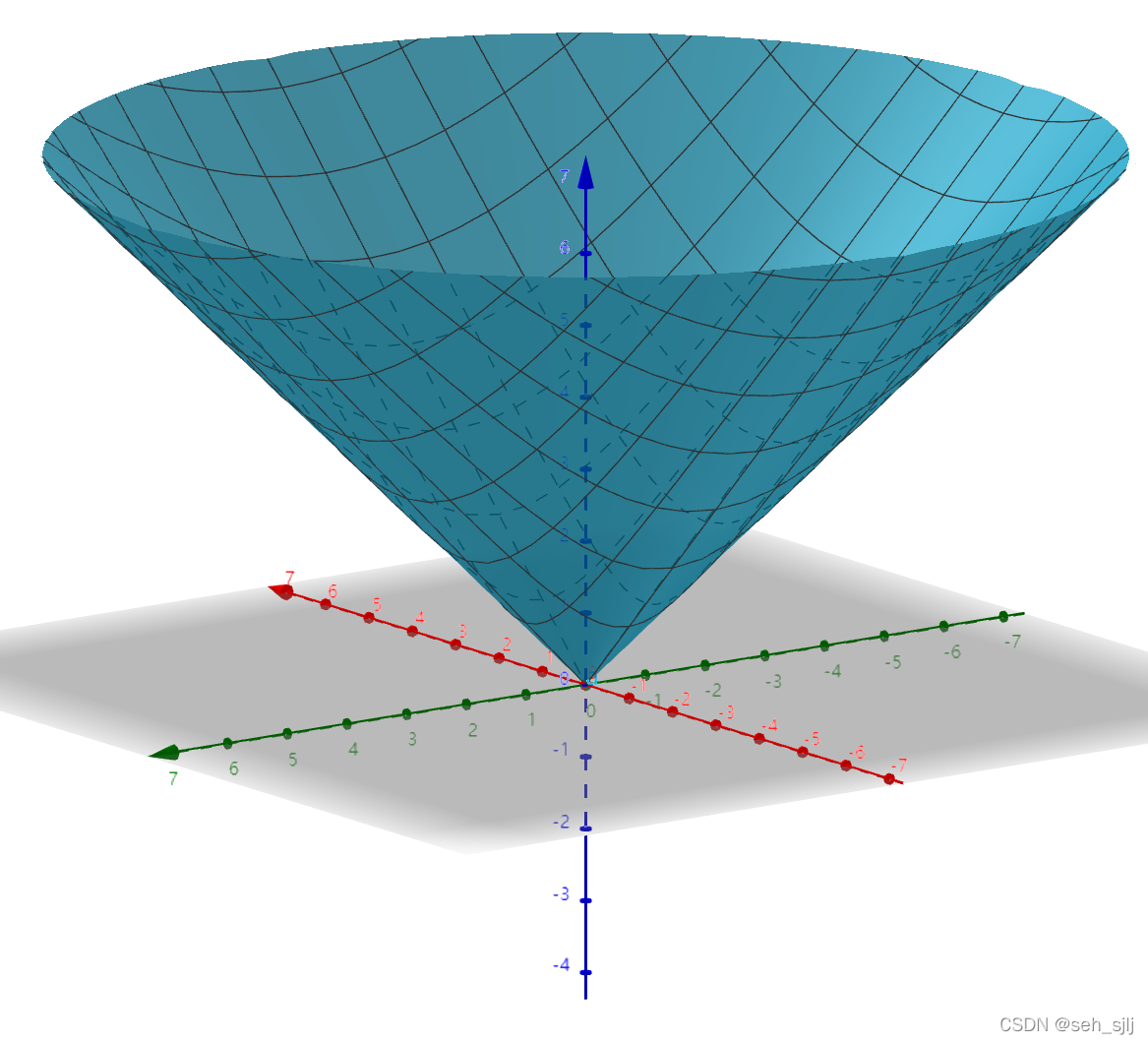
这个很容易理解，跟一元函数一样。 例如 f ( x , y ) = ∣ x ∣ f(x,y)=|x| f(x,y)=∣x∣，在 ( 0 , 0 ) (0,0) (0,0)连续，但 f x ( 0 , 0 ) = d ∣ x ∣ d x f_x(0,0)=\frac{\text{d}|x|}{\text{d}x} fx​(0,0)=dxd∣x∣​不存在。 再例如， f ( x , y ) = x 2 + y 2 f(x,y)=\sqrt{x^2+y^2} f(x,y)=x2+y2 ​，其在 ( 0 , 0 ) (0,0) (0,0)点显然连续，但 f x ( 0 , 0 ) = lim ⁡ x → 0 ∣ x ∣ x f_x(0,0)=\lim_{x\to0}\frac{|x|}{x} fx​(0,0)=x→0lim​x∣x∣​不存在， f y ( 0 , 0 ) f_y(0,0) fy​(0,0)同理也不存在。 用Geogebra画图可以看出这个函数的图像是锥形，在 ( 0 , 0 ) (0,0) (0,0)点是尖的：

这个性质跟一元函数有很大差异。对于二元函数，偏导数存在是很弱的条件，甚至连极限都有可能不存在。 例子： f ( x , y ) = { x y x 2 + y 2 , x 2 + y 2 ≠ 0 0 , x 2 + y 2 = 0 f(x,y)=\begin{cases}\frac{xy}{x^2+y^2},&x^2+y^2\ne0\\0,&x^2+y^2=0\end{cases} f(x,y)={x2+y2xy​,0,​x2+y2=0x2+y2=0​它在 ( 0 , 0 ) (0,0) (0,0)点的两个偏导数都存在： f x ( 0 , 0 ) = f y ( 0 , 0 ) = 0 f_x(0,0)=f_y(0,0)=0 fx​(0,0)=fy​(0,0)=0但是它在 ( 0 , 0 ) (0,0) (0,0)点的极限不存在，以 y = k x y=kx y=kx的路径逼近 ( 0 , 0 ) (0,0) (0,0)得 lim ⁡ x → 0 , y = k x x y x 2 + y 2 = k 1 + k 2 \lim_{x\to0,y=kx}\frac{xy}{x^2+y^2}=\frac{k}{1+k^2} x→0,y=kxlim​x2+y2xy​=1+k2k​随着 k k k的变化而变化，所以 lim ⁡ ( x , y ) → ( 0 , 0 ) f ( x , y ) \lim_{(x,y)\to(0,0)}f(x,y) (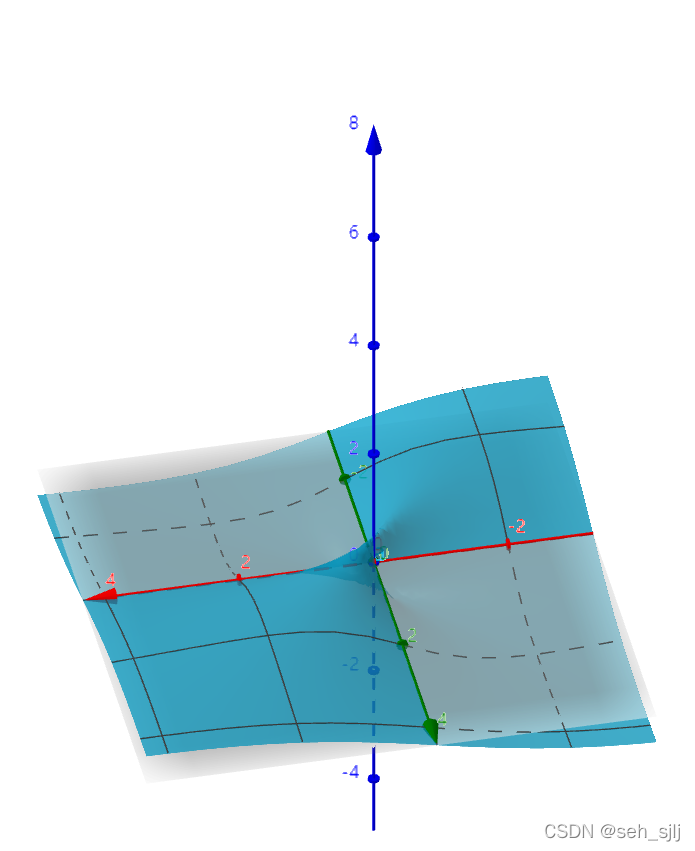x,y)→(0,0)lim​f(x,y)不存在。 画图看出这个函数在 ( 0 , 0 ) (0,0) (0,0)点呈现一个很奇怪的样子：

定理1（可微的必要条件） 设函数 z = f ( x , y ) z=f(x,y) z=f(x,y)在 ( x 0 , y 0 ) (x_0,y_0) (x0​,y0​)处可微，则 (1) f f f在 ( x 0 , y 0 ) (x_0,y_0) (x0​,y0​)处连续； (2) f f f在 ( x 0 , y 0 ) (x_0,y_0) (x0​,y0​)处的两个偏导数都存在，且有 d f ( x 0 , y 0 ) = f x ( x 0 , y 0 ) d x + f y ( x 0 , y 0 ) d y \text{d}f(x_0,y_0)=f_x(x_0,y_0)\text{d}x+f_y(x_0,y_0)\text{d}y df(x0​,y0​)=fx​(x0​,y0​)dx+fy​(x0​,y0​)dy。 证明： (1) 当 f f f在 ( x 0 , y 0 ) (x_0,y_0) (x0​,y0​)处可微时，存在常数 a 1 , a 2 a_1,a_2 a1​,a2​使得 Δ z = a 1 Δ x + a 2 Δ y + o ( ρ ) \Delta z=a_1\Delta x+a_2\Delta y+o(\rho) Δz=a1​Δx+a2​Δy+o(ρ)，其中 ρ = ( Δ x ) 2 + ( Δ y ) 2 \rho=\sqrt{(\Delta x)^2+(\Delta y)^2} ρ=(Δx)2+(Δy)2 ​。令 ρ → 0 \rho\to0 ρ→0，即 Δ x → 0 \Delta x\to0 Δx→0且 Δ y → 0 \Delta y\to0 Δy→0，得 lim ⁡ ρ → 0 Δ z = 0 \lim_{\rho\to0}\Delta z=0 ρ→0lim​Δz=0或 lim ⁡ Δ x → 0 , Δ y → 0 f ( x 0 + Δ x , y 0 + Δ y ) = lim ⁡ Δ x → 0 , Δ y → 0 [ f ( x 0 , y 0 ) + Δ z ] = f ( x 0 , y 0 ) \lim_{\Delta x\to0,\Delta y\to0}f(x_0+\Delta x,y_0+\Delta y)=\lim_{\Delta x\to0,\Delta y\to0}[f(x_0,y_0)+\Delta z]=f(x_0,y_0) Δx→0,Δy→0lim​f(x0​+Δx,y0​+Δy)=Δx→0,Δy→0lim​[f(x0​,y0​)+Δz]=f(x0​,y0​)因此 f f f在 ( x 0 , y 0 ) (x_0,y_0) (x0​,y0​)处连续。 (2) 由可微的定义， f f f满足 f ( x 0 + Δ x , y 0 + Δ y ) − f ( x 0 , y 0 ) = a 1 Δ x + a 2 Δ y + o ( ρ ) f(x_0+\Delta x,y_0+\Delta y)-f(x_0,y_0)=a_1\Delta x+a_2\Delta y+o(\rho) f(x0​+Δx,y0​+Δy)−f(x0​,y0​)=a1​Δx+a2​Δy+o(ρ)取 Δ y = 0 \Delta y=0 Δy=0，则有 ρ = ∣ Δ x ∣ \rho=|\Delta x| ρ=∣Δx∣，上式变为 f ( x 0 + Δ x , y 0 ) − f ( x 0 , y 0 ) = a 1 + o ( ∣ Δ x ∣ ) f(x_0+\Delta x,y_0)-f(x_0,y_0)=a_1+o(|\Delta x|) f(x0​+Δx,y0​)−f(x0​,y0​)=a1​+o(∣Δx∣)两边除以 Δ x \Delta x Δx并取极限得 lim ⁡ Δ x → 0 f ( x 0 + Δ x , y 0 ) − f ( x 0 , y 0 ) Δ x = lim ⁡ Δ x → 0 [ a 1 + o ( ∣ Δ x ∣ ) Δ x ] = a 1 \lim_{\Delta x\to0}\frac{f(x_0+\Delta x,y_0)-f(x_0,y_0)}{\Delta x}=\lim_{\Delta x\to0}\left[a_1+\frac{o(|\Delta x|)}{\Delta x}\right]=a_1 Δx→0lim​Δxf(x0​+Δx,y0​)−f(x0​,y0​)​=Δx→0lim​[a1​+Δxo(∣Δx∣)​]=a1​即 f x ( x 0 , y 0 ) = a 1 f_x(x_0,y_0)=a_1 fx​(x0​,y0​)=a1​。 同理，取 Δ x = 0 \Delta x=0 Δx=0得 f y ( x 0 , y 0 ) = a 2 f_y(x_0,y_0)=a_2 fy​(x0​,y0​)=a2​。∎

从这里我们可以看出，可微是很强得条件，远比偏导数存在要强。

然而，这个条件仅仅是必要条件。我们举一个例子 f ( x , y ) = { x y x 2 + y 2 , x 2 + y 2 ≠ 0 0 , x 2 + y 2 = 0 f(x,y)=\begin{cases}\frac{xy}{\sqrt{x^2+y^2}},&x^2+y^2\ne0\\0,&x^2+y^2=0\end{cases} f(x,y)={x2+y2 ​xy​,0,​x2+y2=0x2+y2=0​它在 ( 0 , 0 ) (0,0) (0,0)点连续，因为 lim ⁡ ( x , y ) → ( 0 , 0 ) ∣ f ( x , y ) − f ( 0 , 0 ) ∣ = lim ⁡ ( x , y ) → ( 0 , 0 ) ∣ f ( x , y ) ∣ ≤ lim ⁡ ( x , y ) → ( 0 , 0 ) x 2 + y 2 2 x 2 + y 2 = 0 \lim_{(x,y)\to(0,0)}|f(x,y)-f(0,0)|=\lim_{(x,y)\to(0,0)}|f(x,y)|\le\lim_{(x,y)\to(0,0)}\frac{x^2+y^2}{2\sqrt{x^2+y^2}}=0 (x,y)→(0,0)lim​∣f(x,y)−f(0,0)∣=(x,y)→(0,0)lim​∣f(x,y)∣≤(x,y)→(0,0)lim​2x2+y2 ​x2+y2​=0两个偏导数也存在： f x ( 0 , 0 ) = f y ( 0 , 0 ) = 0 f_x(0,0)=f_y(0,0)=0 fx​(0,0)=fy​(0,0)=0但不可微。因为如果可微，那么 Δ f − f x ( 0 , 0 ) Δ x − f y ( 0 , 0 ) Δ y = o ( ρ ) \Delta f-f_x(0,0)\Delta x-f_y(0,0)\Delta y=o(\rho) Δf−fx​(0,0)Δx−fy​(0,0)Δy=o(ρ)。然而 lim ⁡ ( x , y ) → ( 0 , 0 ) Δ f ρ = lim ⁡ ( x , y ) → ( 0 , 0 ) x y x 2 + y 2 \lim_{(x,y)\to(0,0)}\frac{\Delta f}{\rho}=\lim_{(x,y)\to(0,0)}\frac{xy}{x^2+y^2} (x,y)→(0,0)lim​ρΔf​=(x,y)→(0,0)lim​x2+y2xy​不存在。也就是说，满足定理1的条件不一定可微。 其函数图像如下：

定理2（可微的充分条件） 设函数 z = f ( x , y ) z=f(x,y) z=f(x,y)在点 ( x 0 , y 0 ) (x_0,y_0) (x0​,y0​)得的某个邻域内有定义，若 f ( x , y ) f(x,y) f(x,y)的两个偏导数 f x ( x , y ) f_x(x,y) fx​(x,y)和 f y ( x , y ) f_y(x,y) fy​(x,y)均在点 ( x 0 , y 0 ) (x_0,y_0) (x0​,y0​)处连续，则该函数在点 ( x 0 , y 0 ) (x_0,y_0) (x0​,y0​)处可微。 证明： Δ z = f ( x 0 + Δ x , y 0 + Δ y ) − f ( x 0 , y 0 ) = [ f ( x 0 + Δ x , y 0 + Δ y ) − f ( x 0 , y 0 + Δ y ) ] + [ f ( x 0 , y 0 + Δ y ) − f ( x 0 , y 0 ) ] \begin{aligned}\Delta z&=f(x_0+\Delta x,y_0+\Delta y)-f(x_0,y_0)\\&=[f(x_0+\Delta x,y_0+\Delta y)-f(x_0,y_0+\Delta y)]+[f(x_0,y_0+\Delta y)-f(x_0,y_0)]\end{aligned} Δz​=f(x0​+Δx,y0​+Δy)−f(x0​,y0​)=[f(x0​+Δx,y0​+Δy)−f(x0​,y0​+Δy)]+[f(x0​,y0​+Δy)−f(x0​,y0​)]​右边的每一项都是一元函数的改变量，故可以采用拉格朗日中值定理（ f ( b ) − f ( a ) = f ′ ( ξ ) ( b − a ) f(b)-f(a)=f'(\xi)(b-a) f(b)−f(a)=f′(ξ)(b−a)），即存在 θ 1 , θ 2 ∈ ( 0 , 1 ) \theta_1,\theta_2\in(0,1) θ1​,θ2​∈(0,1)使得 Δ z = f x ( x 0 + θ 1 Δ x , y 0 + Δ y ) Δ x + f y ( x 0 , y 0 + θ 2 Δ y ) Δ y \Delta z=f_x(x_0+\theta_1\Delta x,y_0+\Delta y)\Delta x+f_y(x_0,y_0+\theta_2\Delta y)\Delta y Δz=fx​(x0​+θ1​Δx,y0​+Δy)Δx+fy​(x0​,y0​+θ2​Δy)Δy由于 f x ( x , y ) f_x(x,y) fx​(x,y)在 ( x 0 , y 0 ) (x_0,y_0) (x0​,y0​)连续，取极限 ρ = ( Δ x ) 2 + ( Δ y ) 2 → 0 \rho=\sqrt{(\Delta x)^2+(\Delta y)^2}\to0 ρ=(Δx)2+(Δy)2 ​→0得 lim ⁡ ρ → 0 f x ( x 0 + θ 1 Δ x , y 0 + Δ y ) = f x ( x 0 , y 0 ) \lim_{\rho\to0}f_x(x_0+\theta_1\Delta x,y_0+\Delta y)=f_x(x_0,y_0) ρ→0lim​fx​(x0​+θ1​Δx,y0​+Δy)=fx​(x0​,y0​)因此有 f x ( x 0 + θ 1 Δ x , y 0 + Δ y ) = f x ( x 0 , y 0 ) + α 1 ( ρ ) f_x(x_0+\theta_1\Delta x,y_0+\Delta y)=f_x(x_0,y_0)+\alpha_1(\rho) fx​(x0​+θ1​Δx,y0​+Δy)=fx​(x0​,y0​)+α1​(ρ)同理有 f y ( x 0 , y 0 + θ 2 Δ y ) = f ( x 0 , y 0 ) + α 2 ( ρ ) f_y(x_0,y_0+\theta_2\Delta y)=f(x_0,y_0)+\alpha_2(\rho) fy​(x0​,y0​+θ2​Δy)=f(x0​,y0​)+α2​(ρ)其中 α 1 , 2 ( ρ ) \alpha_{1,2}( \rho) α1,2​(ρ)是 ρ \rho ρ的高阶无穷小。整理得 Δ z = f ( x 0 + Δ x , y 0 + Δ y ) − f ( x 0 , y 0 ) = [ f ( x 0 + Δ x , y 0 + Δ y ) − f ( x 0 , y 0 + Δ y ) ] + [ f ( x 0 , y 0 + Δ y ) − f ( x 0 , y 0 ) ] = [ f x ( x 0 , y 0 ) + α 1 ( ρ ) ] Δ x + [ f ( x 0 , y 0 ) + α 2 ( ρ ) ] Δ y = f x ( x 0 , y 0 ) Δ x + f y ( x 0 , y 0 ) Δ y + α 1 ( ρ ) Δ x + α 2 ( ρ ) Δ y \begin{aligned}\Delta z&=f(x_0+\Delta x,y_0+\Delta y)-f(x_0,y_0)\\&=[f(x_0+\Delta x,y_0+\Delta y)-f(x_0,y_0+\Delta y)]+[f(x_0,y_0+\Delta y)-f(x_0,y_0)]\\&=[f_x(x_0,y_0)+\alpha_1(\rho)]\Delta x+[f(x_0,y_0)+\alpha_2(\rho)]\Delta y\\&=f_x(x_0,y_0)\Delta x+f_y(x_0,y_0)\Delta y+\alpha_1(\rho)\Delta x+\alpha_2(\rho)\Delta y\end{aligned} Δz​=f(x0​+Δx,y0​+Δy)−f(x0​,y0​)=[f(x0​+Δx,y0​+Δy)−f(x0​,y0​+Δy)]+[f(x0​,y0​+Δy)−f(x0​,y0​)]=[fx​(x0​,y0​)+α1​(ρ)]Δx+[f(x0​,y0​)+α2​(ρ)]Δy=fx​(x0​,y0​)Δx+fy​(x0​,y0​)Δy+α1​(ρ)Δx+α2​(ρ)Δy​只需证明后面两项是 ρ \rho ρ的高阶无穷小。而 Δ x ≤ ρ \Delta x\le\rho Δx≤ρ， Δ y ≤ ρ \Delta y\le\rho Δy≤ρ，所以 ∣ α 1 ( ρ ) Δ x + α 2 ( ρ ) Δ y ∣ ≤ ∣ α 1 ( ρ ) + α 2 ( ρ ) ∣ ρ |\alpha_1(\rho)\Delta x+\alpha_2(\rho)\Delta y|\le|\alpha_1(\rho)+\alpha_2(\rho)|\rho ∣α1​(ρ)Δx+α2​(ρ)Δy∣≤∣α1​(ρ)+α2​(ρ)∣ρ， lim ⁡ ρ → 0 ∣ α 1 ( ρ ) Δ x + α 2 ( ρ ) Δ y ρ ∣ = lim ⁡ ρ → 0 α 1 ( ρ ) + α 2 ( ρ ) = o ( ρ ) \lim_{\rho\to0}\left|\frac{\alpha_1(\rho)\Delta x+\alpha_2(\rho)\Delta y}{\rho}\right|=\lim_{\rho\to0}\alpha_1(\rho)+\alpha_2(\rho)=o(\rho) ρ→0lim​ ​ρα1​(ρ)Δx+α2​(ρ)Δy​ ​=ρ→0lim​α1​(ρ)+α2​(ρ)=o(ρ)于是 α 1 ( ρ ) Δ x + α 2 ( ρ ) Δ y \alpha_1(\rho)\Delta x+\alpha_2(\rho)\Delta y α1​(ρ)Δx+α2​(ρ)Δy是 ρ \rho ρ的高阶无穷小。因此有 Δ z = f x ( x 0 , y 0 ) Δ x + f y ( x 0 , y 0 ) Δ y + o ( ρ ) \Delta z=f_x(x_0,y_0)\Delta x+f_y(x_0,y_0)\Delta y+o(\rho) Δz=fx​(x0​,y0​)Δx+fy​(x0​,y0​)Δy+o(ρ)即 f f f在 ( x 0 , y 0 ) (x_0,y_0) (x0​,y0​)处可微。∎

注意：这只是充分条件。有些函数，例如 f ( x , y ) = { ( x 2 + y 2 ) sin ⁡ 1 x 2 + y 2 , x 2 + y 2 ≠ 0 0 , x 2 + y 2 = 0 f(x,y)=\begin{cases}(x^2+y^2)\sin{\frac{1}{x^2+y^2}},&x^2+y^2\ne0\\0,&x^2+y^2=0\end{cases} f(x,y)={(x2+y2)sinx2+y21​,0,​x2+y2=0x2+y2=0​它在 ( 0 , 0 ) (0,0) (0,0)处可微，但 f x ( x , y ) f_x(x,y) fx​(x,y)与 f y ( x , y ) f_y(x,y) fy​(x,y)在 ( 0 , 0 ) (0,0) (0,0)处间断。

另外， f x ( x , y ) , f y ( x , y ) f_x(x,y),f_y(x,y) fx​(x,y),fy​(x,y)是二元函数，它们连续是指满足二元函数连续的条件，而不仅仅是在 x x x方向或在 y y y方向上连续。

这是定理1和定理2结合起来后一个很显然的推论。

定理3 若 f ( x , y ) f(x,y) f(x,y)在点 ( x 0 , y 0 ) (x_0,y_0) (x0​,y0​)可微，则函数 f f f在点 ( x 0 , y 0 ) (x_0,y_0) (x0​,y0​)沿任意 l \bm l l方向的方向导数均存在，且 ∂ f ∂ l ∣ x 0 , y 0 = f x ( x 0 , y 0 ) cos ⁡ α + f y ( x 0 , y 0 ) cos ⁡ β \left.\frac{\partial f}{\partial\bm l}\right|_{x_0,y_0}=f_x(x_0,y_0)\cos\alpha+f_y(x_0,y_0)\cos\beta ∂l∂f​ ​x0​,y0​​=fx​(x0​,y0​)cosα+fy​(x0​,y0​)cosβ其中 l \bm l l方向上的单位向量是 e l = ( cos ⁡ α , cos ⁡ β ) \bm e_l=(\cos\alpha,\cos\beta) el​=(cosα,cosβ)。 证明：由定理1，当 ( x , y ) → ( 0 , 0 ) (x,y)\to(0,0) (x,y)→(0,0)时，有 f ( x , y ) − f ( x 0 , y 0 ) = f x ( x 0 , y 0 ) Δ x + f y ( x 0 , y 0 ) Δ y + o ( ρ ) f(x,y)-f(x_0,y_0)=f_x(x_0,y_0)\Delta x+f_y(x_0,y_0)\Delta y+o(\rho) f(x,y)−f(x0​,y0​)=fx​(x0​,y0​)Δx+fy​(x0​,y0​)Δy+o(ρ)令 ( x , y ) = ( x 0 , y 0 ) + t e l = ( x 0 , y 0 ) + ( t cos ⁡ α , t cos ⁡ β ) (x,y)=(x_0,y_0)+t\bm e_l=(x_0,y_0)+(t\cos\alpha,t\cos\beta) (x,y)=(x0​,y0​)+tel​=(x0​,y0​)+(tcosα,tcosβ)，即 Δ x = t cos ⁡ α , Δ y = t cos ⁡ β , ∣ t ∣ = ( Δ x ) 2 + ( Δ y ) 2 \Delta x=t\cos\alpha,\Delta y=t\cos\beta,|t|=\sqrt{(\Delta x)^2+(\Delta y)^2} Δx=tcosα,Δy=tcosβ,∣t∣=(Δx)2+(Δy)2 ​，可得 f ( x 0 , y 0 ) = f x ( x 0 , y 0 ) t cos ⁡ α + f y ( x 0 , y 0 ) t cos ⁡ β + o ( ρ ) f(x_0,y_0)=f_x(x_0,y_0)t\cos\alpha+f_y(x_0,y_0)t\cos\beta+o(\rho) f(x0​,y0​)=fx​(x0​,y0​)tcosα+fy​(x0​,y0​)tcosβ+o(ρ)由方向导数的定义有 ∂ f ∂ l ∣ x 0 , y 0 = lim ⁡ t → 0 f ( x 0 + t cos ⁡ α , y 0 + t cos ⁡ β ) − f ( x 0 , y 0 ) t = lim ⁡ t → 0 f x ( x 0 , y 0 ) t cos ⁡ α + f y ( x 0 , y 0 ) t cos ⁡ β + o ( ∣ t ∣ ) t = f x ( x 0 , y 0 ) cos ⁡ α + f y ( x 0 , y 0 ) cos ⁡ β \begin{aligned}\left.\frac{\partial f}{\partial\bm l}\right|_{x_0,y_0}&=\lim_{t\to0}\frac{f(x_0+t\cos\alpha,y_0+t\cos\beta)-f(x_0,y_0)}{t}\\&=\lim_{t\to0}\frac{f_x(x_0,y_0)t\cos\alpha+f_y(x_0,y_0)t\cos\beta+o(|t|)}{t}\\&=f_x(x_0,y_0)\cos\alpha+f_y(x_0,y_0)\cos\beta\end{aligned} ∂l∂f​ ​x0​,y0​​​=t→0lim​tf(x0​+tcosα,y0​+tcosβ)−f(x0​,y0​)​=t→0lim​tfx​(x0​,y0​)tcosα+fy​(x0​,y0​)tcosβ+o(∣t∣)​=fx​(x0​,y0​)cosα+fy​(x0​,y0​)cosβ​证毕。∎

综合以上所有讨论，我们将各个条件之间的关系理成下面这张图：

可以看出偏导数连续是最强的条件，可微是很强的条件，（任意方向）偏导数存在是很弱的条件。