| 机器学习算法 08 | 您所在的位置:网站首页 › 支持向量机应用实例 › 机器学习算法 08 |
机器学习算法 08
|
文章目录
系列文章支持向量机SVM算法1 SVM算法简介1.1 引入1.2 算法定义
2 SVM算法原理2.1 线性可分支持向量机2.2 SVM计算过程与算法步骤(有点难,我也没理解透,建议跳过)推导目标函数目标函数求解拉格朗日乘数法对偶问题整体流程确定
3 SVM的损失函数4 SVM的核方法4.1 什么是核函数4.2 常见核函数
5 SVM回归6 SVM算法API介绍6.1 SVM算法API综述6.2 SVC6.3 NuSVC6.4 LinearSVC
7 案例:数字识别器7.1 案例背景介绍7.2 数据介绍7.3 案例实现确定最优参数结果预测
8 SVM总结
系列文章
机器学习算法 01 —— K-近邻算法(数据集划分、归一化、标准化) 机器学习算法 02 —— 线性回归算法(正规方程、梯度下降、模型保存) 机器学习算法 03 —— 逻辑回归算法(精确率和召回率、ROC曲线和AUC指标、过采样和欠采样) 机器学习算法 04 —— 决策树(ID3、C4.5、CART,剪枝,特征提取,回归决策树) 机器学习算法 05 —— 集成学习(Bagging、随机森林、Boosting、AdaBost、GBDT) 机器学习算法 06 —— 聚类算法(k-means、算法优化、特征降维、主成分分析PCA) 机器学习算法 07 —— 朴素贝叶斯算法(拉普拉斯平滑系数、商品评论情感分析案例) 机器学习算法 08 —— 支持向量机SVM算法(核函数、手写数字识别案例) 机器学习算法 09 —— EM算法(马尔科夫算法HMM前置学习,EM用硬币案例进行说明) 机器学习算法 10 —— HMM模型(马尔科夫链、前向后向算法、维特比算法解码、hmmlearn) 支持向量机SVM算法学习目标: 了解什么是SVM算法掌握SVM算法的原理知道SVM算法的损失函数知道SVM算法的核函数了解SVM算法在回归问题中的使⽤应⽤SVM算法实现⼿写数字识别器 1 SVM算法简介 1.1 引入案例来源:http://bytesizebio.net/2014/02/05/support-vector-machines-explained-well/ 视频演示:https://www.youtube.com/watch?v=3liCbRZPrZA 桌上有两种颜色的球,我们需要用一根棍子将它们区分开,并且要求之后添加球也能继续适用。
显而易见,我们可以这样放!
接着,我们继续添加球,但似乎有一个红球被分错了类。
此时我们可以把棍子变得更粗,稍微改变下角度,让棍子的两边有更大的空隙(最大间隙)。
这样即使再放更多的球,这跟棍子依然是一个比较好的分界线。
如果我们加大难度,变成下面这样的情况后该如何分类呢?
我们将这个二维图像转换到三维,用力在桌上一拍!这时,我们可以用一张纸去分类!
但我们试图用二维的视角去看这个划分的纸,那就是一条曲线。
上面这些东西在学术上是另一种说法: 球 —— 数据 [data]棍子 —— 分类器 [classifier]最大间隙 —— 最优化 [optimization]拍桌子 —— 核方法 [kernelling]纸 —— 超平面 [hyperplane]1.2 算法定义 SVM(supported vector machine,⽀持向量机):找到⼀个超平⾯使样本分成两类,并且间隔最⼤。 SVM能够执⾏线性或⾮线性分类、回归,甚⾄是异常值检测任务。它是机器学习领域最受欢迎的模型之⼀,特别适⽤于中⼩型复杂数据集的分类。
超平⾯最⼤间隔 下面左图显示了三种可能的线性分类器的决策边界,虚线代表的模型表现⾮常糟糕,甚⾄都⽆法正确实现分类。 其余两个模型(红线和紫线)在训练集上表现比较完美,但是它们的决策边界与实例过于接近,导致在⾯对新实例时,表现可能不会太好。 而下面右图中的实线代表不仅分离了两个类别,且尽可能远离最近的训练实例。
硬间隔 在上⾯我们使⽤超平⾯进⾏分割数据的过程中,如果我们严格地让所有实例都不在最⼤间隔之间,只位于正确的⼀边,这就是硬间隔分类。 硬间隔分类有两个问题:⾸先,它只在数据是线性可分离的时候才有效;其次,它对异常值⾮常敏感。 例如,下面这两幅图,它们是鸢尾花数据。左图有一个绿点在蓝点中间,无法找出硬间隔;右图虽然找出一个硬间隔,但间隔太窄无法无法有效泛化。
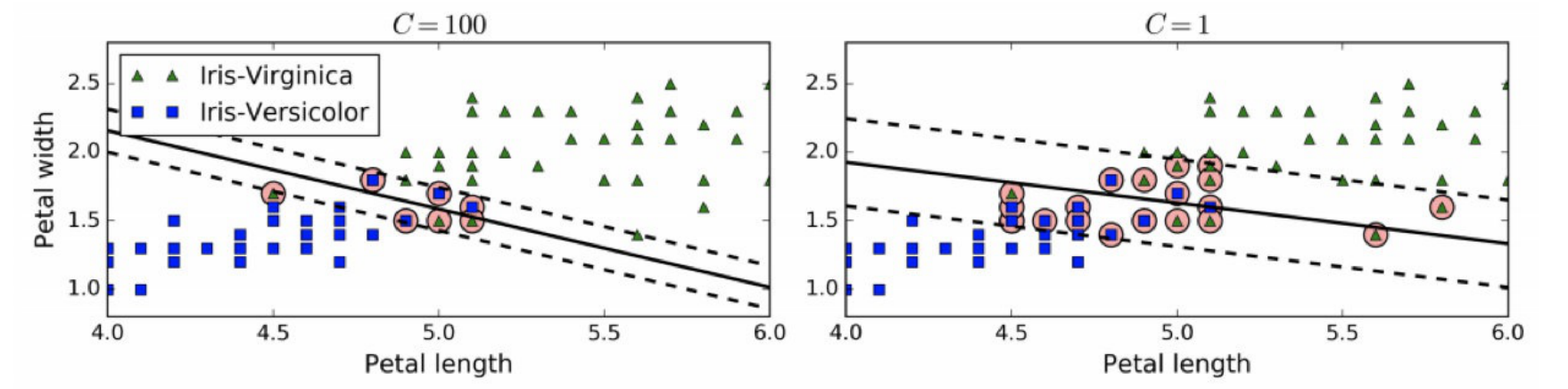
软间隔 为了避免硬间隔的问题,软间隔应运而生。软间隔的⽬标是尽可能在保持最⼤间隔宽阔和限制间隔违例(即限制位于最⼤间隔之外,甚⾄在错误的⼀边的实例数量)之间找到良好的平衡。
在Scikit-Learn的SVM类中,可以通过超参数C来控制这个平衡:C值越⼩则间隔越宽,但是间隔违例也会越多。 上图显示了在⼀个⾮线性可分离数据集上,两个软间隔SVM分类器各⾃的决策边界和间隔。 左边使⽤了⾼C值,分类器的错误样本(间隔违例)较少,但是间隔也较⼩。右边使⽤了低C值,间隔⼤了很多,但是位于间隔上的实例也更多。 看起来第⼆个分类器的泛化效果更好,因为⼤多数间隔违例实际上都位于决策边界正确的⼀边,所以即便是在该训练集上,它做出的错误预测也会更少。 2 SVM算法原理 2.1 线性可分支持向量机 假设特征空间上的一个线性可分离训练集为: T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } x i ∈ R n , y i ∈ { + 1 , − 1 } , i = 1 , 2 , . . . N T= \lbrace (x_1,y_1),(x_2,y_2),...,(x_N,y_N) \rbrace \\ x_i \in R^n,y_i \in \lbrace +1, -1 \rbrace,i=1,2,...N T={(x1,y1),(x2,y2),...,(xN,yN)}xi∈Rn,yi∈{+1,−1},i=1,2,...N 其中 ( x i , y i ) (x_i,y_i) (xi,yi)称为样本点, x i x_i xi是第i个样本, y i y_i yi为 x i x_i xi的标记【 y i = 1 时 , x i 为 正 例 ; y i = − 1 时 , x i 为 负 例 y_i=1时,x_i为正例;y_i=-1时,x_i为负例 yi=1时,xi为正例;yi=−1时,xi为负例】 为什么标记要为+1、-1呢? 其实没有太多原理,只是一个标记,我们也可以用其他数字来标记,但为了方便后面计算 y i y j = y i ∗ y j \frac{y_i}{y_j}=y_i*y_j yjyi=yi∗yj,取+1、-1比较好。
给出了上面的线性可分离训练数据集,我们可以通过间隔最大化得到分离超平面: y ( x ) = w T Φ ( x ) + b y(x)=w^T \Phi(x)+b y(x)=wTΦ(x)+b 相应的分类决策函数为: f ( x ) = s i g n ( w T Φ ( x ) + b ) f(x)=sign(w^T\Phi(x)+b) f(x)=sign(wTΦ(x)+b),这个决策函数就被称为线性可分支持向量机。 这里说明下 Φ ( x ) \Phi(x) Φ(x),前面我们引入SVM时举例了一个“拍桌子”的行为,能将二维的球“拍”到三维中的核函数就是 Φ ( x ) \Phi(x) Φ(x),它的作用就是将 x x x投影到更高维度。 例如我们看到的特征有2个, x 1 x_1 x1和 x 2 x_2 x2,它们组成了一个线性函数 w 1 x 1 + w 2 x 2 w_1x_1+w_2x_2 w1x1+w2x2 可能这两个特征并不能很好地描述数据,于是我们进行维度转化,变成 w 1 x 1 + w 2 x 2 + w 3 x 1 x 2 + w 4 x 1 2 + w 5 x 2 2 w_1x_1+w_2x_2+w_3x_1x_2+w_4x_1^2+w_5x_2^2 w1x1+w2x2+w3x1x2+w4x12+w5x22 于是我们就多了三个特征,而这个就是笼统地描述x的映射。 最简单直接的就是 Φ ( x ) = x \Phi(x)=x Φ(x)=x 上面这个表达式就也就是一个超平面 y ( x ) y(x) y(x),本质上其实就是让我们求出一组参数 ( w , b ) (w,b) (w,b),使其构建的超平面函数能最优地分离两个集合。 例如下面这幅图就是一个超平面(硬间隔):
从这幅图可以看出, w w w其实是一个法向量(两条虚线上的点垂直到实线上距离最近),而b决定超平面和原点的距离。 再例如下面这幅图(软间隔):阴影部分是⼀个“过渡带”,“过渡带”的边界是集合中离超平⾯最近的样本点落在的地⽅。
2.2 SVM计算过程与算法步骤(有点难,我也没理解透,建议跳过) 推导目标函数 我们知道了支持向量机是什么,现在我们要去寻找一个最优的超平面,再次之前我们需要建立一个目标函数。 再来看看超平面表达式: y ( x ) = w T Φ ( x ) + b y(x)=w^T\Phi(x)+b y(x)=wTΦ(x)+b,为了方便,我们设 Φ ( x ) = x \Phi(x)=x Φ(x)=x。 在样本空间中,划分超平面可以通过如下线性方程来描述: w T x + b = 0 w^Tx+b=0 wTx+b=0 w = ( w 1 , w 2 , . . . , w d ) w=(w_1,w_2,...,w_d) w=(w1,w2,...,wd)为法向量,决定了超平面的方向b是位移项,决定了超平面和原点之间的距离显然,划分超平面可以被法向量 w w w和位移项b确定,我们把其记为 ( w , b ) (w,b) (w,b)因此,样本空间中任意点x到超平面 ( w , b ) (w,b) (w,b)的距离可以写为: γ = ∣ w T x + b ∣ ∣ ∣ w ∣ ∣ \gamma = \frac{|w^Tx+b|}{||w||} γ=∣∣w∣∣∣wTx+b∣ 假设超平面 ( w , b ) (w,b) (w,b)能将训练样本正确分类,那么对于 ( x i , y i ) ∈ D (x_i,y_i) \in D (xi,yi)∈D 若 y i = + 1 y_i=+1 yi=+1,则有 w T x i + b > 0 w^Tx_i+b>0 wTxi+b>0若 y i = − 1 y_i=-1 yi=−1,则有 w T x i + b < 0 w^Tx_i+bwTxi+b≥+1wTxi+b≤−1yi=+1yi=−1 即 有 m a x ( w , b ) = 2 ∣ ∣ w ∣ ∣ 使 得 y i ( w T x i + b ) ≥ 1 , i = 1 , 2 , . . . , m 有max_{(w,b)}=\frac{2}{||w||}\\ 使得 \ \ \ y_i(w^Tx_i+b) \ge 1,i=1,2,...,m 有max(w,b)=∣∣w∣∣2使得 yi(wTxi+b)≥1,i=1,2,...,m 显然,为了最大化间隔,也就是需要最大化 1 ∣ ∣ w ∣ ∣ \frac{1}{||w||} ∣∣w∣∣1,这等价于最小化 ∣ ∣ w ∣ ∣ 2 ||w||^2 ∣∣w∣∣2,于是上式可以重写为: 有 m i n ( w , b ) = 1 2 ∣ ∣ w ∣ ∣ 2 使 得 y i = ( w T x + b ) ≥ 1 , i = 1 , 2 , . . . m 有min_{(w,b)}=\frac{1}{2}||w||^2 \\ 使得 y_i=(w^Tx+b) \ge 1,i=1,2,...m 有min(w,b)=21∣∣w∣∣2使得yi=(wTx+b)≥1,i=1,2,...m 这就是支持向量机的基本型。
目标函数求解 拉格朗日乘数法 到了这一步,终于把目标函数给建立起来了,接下来就是求目标函数的最优值。由于目标函数带有一个约束条件,所以我们可以用拉格朗日乘数法求解。【没错,就是高数里面的那个】 什么是拉格朗日乘数法呢? 拉格朗日乘数法(Lagrange multipliers)是一种寻找多元函数在一组约束下的极值的方法,这种方法可以将d个变量和k个约束条件的最优化问题转化为具有d+k个变量的无约束优化问题。【了解它作用就好,不必深究】
想要深入了解,可以看下面拉格朗日乘数法例子 以包含⼀个变量⼀个约束的简单优化问题为例,我们的⽬标函数是 f ( x ) = x 2 + 4 x − 1 f(x) = x^2 + 4x − 1 f(x)=x2+4x−1,讨论两种约束条件g(x): 在满⾜ x ≤ − 1 x\le−1 x≤−1约束条件下求⽬标函数的最⼩值; 在满⾜ x ≥ − 1 x\ge−1 x≥−1约束条件下求⽬标函数的最⼩值。
我们可以直观的从图中得到, 对于约束 1) 使⽬标值f(x)最⼩的最优解是x=−2; 对于约束 2) 使⽬标值f(x)最⼩的最优解是x=−1。
下面我们用拉格朗日乘数法求解。 当没有约束的时候,我们可以直接令⽬标函数的导数为0,求最优值。 可现在有约束,那怎么边考虑约束边求⽬标函数最优值呢? 最直观的办法是把约束放进⽬标函数⾥,由于本例中只有⼀个约束,所以引⼊⼀个朗格朗⽇乘⼦λ,构造⼀个新的函数,拉格朗⽇函数 h ( x ) = f ( x ) + λ g ( x ) h(x) = f(x) + \lambda g(x) h(x)=f(x)+λg(x)该拉格朗⽇函数h(x)最优解可能在g(x) |
【本文地址】