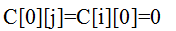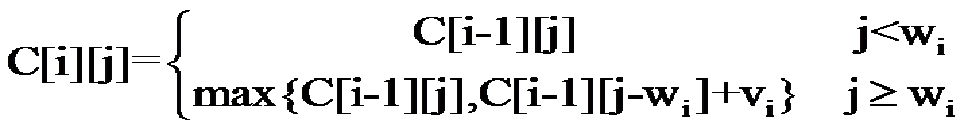西北农林科技大学2020年算法分析与设计实验二

#西北农林科技大学2020年算法分析与设计实验二| 来源: 网络整理| 查看: 265

实验二基于动态规划方法求解0-1背包等问题实验内容

本实验要求基于算法设计与分析的一般过程（即待求解问题的描述、算法设计、算法描述、算法正确性证明、算法分析、算法实现与测试），在针对0-1背包问题求解的实践中理解动态规划 (Dynamic Programming, DP) 方法的思想、求解策略及步骤。作为挑战：可以完成基于跳跃点的改进算法，以支持连续型物品重量/背包容量且提高算法的效率。

实验目的理解动态规划方法的核心思想以及动态规划方法的求解过程；从算法分析与设计的角度，对0-1背包问题的基于DP法求解有更进一步的理解。环境要求

对于环境没有特别要求。对于算法实现，可以自由选择C, C++, Java，甚至于其他程序设计语言如Python等。

我选择c++语言作为此算法的实现语言

实验结果步骤1：理解问题，给出问题的描述。

n个物品和1个背包。对物品i，其价值为vi，重量为wi，背包容量为W。如何选取物品装入背包，使背包中所装入的物品的总价值最大？其中，wi, W都是正整数。

给定一个背包，已知背包的最大承重为 packageWeight ，再给出若干件(numbers件)物品，已经每件物品的重量和对应的价值。

物品的重量存储在weight[]数组中，物品的价值存储在value[]数组中。

现在要求：应该挑选哪几件物品，使得背包装下最大的价值（P.S.：装的物品的重量不能超过背包的承重）

最后打印出了装入了哪几件物品公式化描述为给定C>0,wi>0,vi>0,1≤i≤n,要求找出n元0-1向量(x1,x2,x3,……,xn),1≤i≤n,使得 ∑ i = 1 n \sum_{i=1}^n ∑i=1nwixi≤C,而且 ∑ i = 1 n \sum_{i=1}^n ∑i=1nwixi≤C达到最大。

约束条件: 在这里插入图片描述

目标函数 max ∑ r = 1 n \sum_{r=1}^n ∑r=1nvixi

步骤2 算法设计，包括策略与数据结构的选择

从规模最大的问题的最优解与其子问题的最优解的关系，一级一级抽象问题的一般表述，得出递归关系式：在这里插入图片描述

包的容量比该商品体积小，装不下，此时的价值与此前i-1个的价值是一样的，即V(i,j)=V(i-1,j)还有足够的容量装该商品，但装了也不一定达到当前最优价值，所以在装与不装之间选择最优的一个，即V(i,j)=max{V(i-1,j),V(i-1,j-w(i))+v(i))} 步骤3 描述算法。希望采用源代码以外的形式，如伪代码或流程图等 KNAPSACK-01-DP(w, v, W) //w为重量，v为价值，W为容量 //C[1..n, 1..n]为最优值 FOR i = 1 TO n C[i,0] = 0 FOR j = 1 TO W C[0,j] = 0 FOR i = 1 TO n FOR j = 1 TO W IF j < w[i] C[i,j] = C[i-1][j] ELSE C[i,j] = MAX{C[i-1][j],C[i-1][j-w[i] + v[i]} RETURN C KNAPSACK-TRACEBACK-01(w,W,C,X) //w为重量，W为容量，C为最优值 //X[1..n]为构建的最优解 n = w.length – 1 j = W //Remained Capacity FOR i = n TO 1 IF C[i][j] == C[i-1][j] X[i] = 0 ELSE X[i] = 1 j -= w[i] RETURN X

在这里插入图片描述

步骤4 算法的正确性证明。需要这个环节，在理解的基础上对算法的正确性给予证明；此题目证明循环不变式,网络上的不变式理解循环不变式步骤5 算法复杂性分析，包括时间复杂性和空间复杂性；时间复杂性：

O(n )

空间复杂性：

O(1)

步骤6 算法实现与测试。附上代码或以附件的形式提交，同时贴上算法运行结果截图; #include #include int **knapack01DP(int *v, int *w, int multiWeight, int n, int **C); //C存放最优解,w为重量，v为价值，W为容量 int max(int a, int b) { return (a > b) ? a : b; } //void traceback(int **C,int *w,int *x,int c); int *knapack01traceback(int *w, int multiWeight, int **C, int *X, int n); int main() { int multiWeight; std::cin >> multiWeight; int n; std::cin >> n; int **C = new int *[n + 1]; for (int i = 0; i for (int j = 0; j value[i] = 0; } value[0] = 0; for (int i = 1; i weight[i] = 0; } weight[0] = 0; for (int i = 1; i X[i] = 0; } C = knapack01DP(value, weight, multiWeight, n, C); X = knapack01traceback(weight, multiWeight, C, X, n); for (int i = 0; i // C[i][j] = 0; std::cout // int **C=new int*[n]; // for (int i = 0; i < n; ++i) { // C[i] = new int[n]; // } for (int i = 1; i C[0][i] = 0; } for (int i = 1; i if (j if (C[i][j] == C[i - 1][j]) X[i] = 0; else { X[i] = 1; j -= w[i]; } } return X; }

在这里插入图片描述

算法改进问题描述算法存在的问题

假设物品的重量wi(1≤i≤n)为整数：

如果wi(1≤i≤n)为连续型的实数，如何枚举？

该算法复杂性目前为O(nW)：

当背包容量W很大时，算法所需的计算时间较多。若W>2n，算法复杂性则为O(n × 2n)。指数级算法的改进

在这里插入图片描述

伪代码希望采用源代码以外的形式，如伪代码或流程图等 KNAPSACK-01-OPT(w, v, W) //w为重量，v为价值，W为容量 //p[1..n, 2]：存放指定i的跳跃点即(j,C[i][j])值对。q[1..n, 2]：如定义 p[0] = {(0, 0)} FOR i = 1 to n q[i-1] = p[i-1] + (w[i],v[i]) p[i] = p[i-1] ∪ q[i-1] PROCESS(p[i],W) //剔除受控/无效的跳跃点 RETURN p BACKTRACK-OPT(w, v, p, n) //w为重量，v为价值，p为跳跃点的值对 //x[1..n]：存放问题的解 j = MAX(p[n][0]); m = MAX(p[n][1]) FOR i = n TO 1 IF (j, m) == p[i-1] + (w[i],v[i]) //其中一个满足 x[i] = 1; j = p[i-1][0]; m = p[i-1][1] ELSE x[i] = 0 RETURN x 算法实现与测试 // 动态规划背包问题跳跃点优化 #include using namespace std; template void Traceback(int n,Type w[],Type v[],Type **p,int *head,int x[]) { Type j = p[head[0]-1][0],m=p[head[0]-1][1]; for(int i=1; i if(p[k][0]+w[i]==j && p[k][1]+v[i]==m) { x[i]=1; j=p[k][0]; m=p[k][1]; break; } } } } template int Knapsack(int n,Type c,Type v[],Type w[],int **p,int x[]) { int *head = new int[n+2]; head[n+1]=0; p[0][0]=0; p[0][1]=0; int left = 0,right = 0,next = 1; head[n]=1; for(int i=n; i>=1; i--) { int k = left; for(int j=left; j p[next][0]=p[k][0]; p[next++][1]=p[k++][1]; } if(k m=p[k][1]; } k++; } if(m>p[next-1][1]) { p[next][0]=y; p[next++][1]=m; } while(k p[next][0]=p[k][0]; p[next++][1]=p[k++][1]; } left = right + 1; right = next - 1; head[i-1] = next; } Traceback(n,w,v,p,head,x); return p[next-1][1]; } int main() { int c; cout p[i] = new int[2]; } cout cout

【本文地址】

公司简介

联系我们