| 数值分析(11):常微分方程的数值解法之Euler法 | 您所在的位置:网站首页 › 截断误差和余项的关系 › 数值分析(11):常微分方程的数值解法之Euler法 |
数值分析(11):常微分方程的数值解法之Euler法
|
常微分方程的数值解法之Euler法
1. 引言2. Euler方法2.1 显式Euler方法2.2 隐式Euler方法2.3 梯形方法
3. 隐式方程的迭代求解4. 预估-校正方法5. 误差分析5.1 显式单步方法误差分析5.2 隐式单步方法误差分析
1. 引言
我们通常遇到的一阶常微分方程初值问题,如下所示:
如何证明上面的微分方程存在解,且解唯一呢?则需要以下的存在唯一性定理:
上面定理中的Lipschitz条件,其定义如下: 那么对于上面存在唯一性定理中,同样可以用充分条件来判断
f
f
f是否满足对
y
y
y的Lipschitz条件,即: 讲述了存在唯一性定理后,接下来来看如何解决无法写出解析表达式的微分方程。一种最朴素的方式就是用直线去逼近,把积分区间分成很多段,每一段都使用直线逼近原曲线,用图像表示即为:
为了方便起见,把 y ( x ) y(x) y(x)在 x n x_n xn处的精确值记为 y ( x n ) y(x_n) y(xn), 其近似值用 y n y_n yn表示。 在求微分方程的数值解时,做以下的归类:
由于是近似,自然要分析误差,误差分为两种,整体截断误差和局部截断误差,这两个定义如下:
两者的区别是:整体截断误差是存在误差累积的,累积前n步的误差;局部截断误差是只计算当前第n步的误差。 2. Euler方法Euler方法就是引言中用直线近似来求解微分方程的方法。 2.1 显式Euler方法所谓“显式”,就是说
y
n
+
1
y_{n+1}
yn+1只在等式左边出现。只要能够求出
y
n
+
1
y_{n+1}
yn+1,根据区间分段结果,直接用直线相连即可。 上面只用到了 y n y_n yn即可求解 y n + 1 y_{n+1} yn+1,因此是单步法。 2.2 隐式Euler方法隐式法就是等式右边出现
y
n
+
1
y_{n+1}
yn+1,可以看到显式和隐式的区别在于切线的斜率选取的问题,选取点
(
x
n
,
y
n
)
(x_n,y_n)
(xn,yn)就是显式,选取点
(
x
n
+
1
,
y
n
+
1
)
(x_{n+1},y_{n+1})
(xn+1,yn+1)就是隐式。
如果把显式和隐式的切线斜率公式相加取均值,就得到了梯形公式,即:
梯形方法和隐式Euler方法都是隐式公式,这就涉及到一个问题,等式左右两边都有未知数 y n + 1 y_{n+1} yn+1,这个等式怎么解? 如果是线性的等式,自然可以通过移项转换变成显式的等式,如果是非线性的等式,可以通过前面《数值分析(3):线性代数方程组的迭代解法》中所述的迭代解法求解。 对于隐式Euler法,即用下式迭代:
对于梯形公式,有迭代公式:
其迭代收敛条件为: 为了消除迭代,出现了预估-校正的方法,先给出粗糙估计然后再给出稍精确的求解,这是微分方程数值解常用方法。 比如改进的Euler方法,即:
这公式称为改进的Euler公式,其精度比 Euler 公式好,比梯形公式稍差些,但是,它是显式方法。 5. 误差分析 5.1 显式单步方法误差分析显式单步方法的通式如下: 当然整体截断误差与整个计算中每步情况有关,但一般求得较为困难,因此先考虑一步的误差。 显式单步法的局部截断误差为:
单步法的阶,用来衡量计算方法的精度: 主局部截断误差,它就相当于泰勒展开中的提取余项的操作,对于 p p p阶方法中的 p + 1 p+1 p+1阶无穷小,它进一步将其细化为 p + 1 p+1 p+1次的项,和 p + 2 p+2 p+2阶无穷小,而 p + 1 p+1 p+1次的项 就是主局部截断误差。
在显式单步方法误差分析中,我们分析了局部截断误差表达式,单步法的阶、主局部截断误差。那么对于隐式法,完全可以类似的定义。 比如对于隐式Euler法: T n + 1 = y ( x n + 1 ) − [ y ( x n ) + h f ( x n + 1 , y ( x n + 1 ) ) ] T_{n+1}=y\left( x_{n+1} \right) -\left[ y\left( x_n \right) +hf\left( x_{n+1},y\left( x_{n+1} \right) \right) \right] Tn+1=y(xn+1)−[y(xn)+hf(xn+1,y(xn+1))] 对其进行泰勒展开化简后得: T n + 1 = y ( x n + 1 ) − [ y ( x n ) + h f ( x n + 1 , y ( x n + 1 ) ) ] = y ( x n + h ) − [ y ( x n ) + h y ′ ( x n + h ) ] = y ( x n ) + h y ′ ( x n ) + h 2 2 ! y ′ ′ ( x n ) + o ( h 3 ) − y ( x n ) − h ( y ′ ( x n ) + h y ′ ′ ( x n ) + o ( h 2 ) ) = − h 2 2 y ′ ′ ( x n ) + o ( h 3 ) T_{n+1}=y\left( x_{n+1} \right) -\left[ y\left( x_n \right) +hf\left( x_{n+1},y\left( x_{n+1} \right) \right) \right] \\ =y\left( x_n+h \right) -\left[ y\left( x_n \right) +hy'\left( x_n+h \right) \right] \\ =y\left( x_n \right) +hy'\left( x_n \right) +\frac{h^2}{2!}y''\left( x_n \right) +o\left( h^3 \right) -y\left( x_n \right) -h\left( y'\left( x_n \right) +hy''\left( x_n \right) +o\left( h^2 \right) \right) \\ =-\frac{h^2}{2}y''\left( x_n \right) +o\left( h^3 \right) Tn+1=y(xn+1)−[y(xn)+hf(xn+1,y(xn+1))]=y(xn+h)−[y(xn)+hy′(xn+h)]=y(xn)+hy′(xn)+2!h2y′′(xn)+o(h3)−y(xn)−h(y′(xn)+hy′′(xn)+o(h2))=−2h2y′′(xn)+o(h3) 因此单步法的阶为:一阶方法 主局部截断误差为: − h 2 2 y ′ ′ ( x n ) -\frac{h^2}{2}y''\left( x_n \right) −2h2y′′(xn) 其他的隐式方法完全可以类比推导,这里就省略不写了。 求积公式的余项和数值解的局部截断误差和主局部截断误差有如下关系,以下关系也是很容易理解的,因为微分方程的数值解就是可以通过求积公式导出,自然它们的余项具有非常相近的形式: 参考文献: 关治,陆金甫《数值方法》 |
【本文地址】


 这个定义很难验证,通常使用以下的充分条件来判断函数是否满足Lipschitz条件,即:
这个定义很难验证,通常使用以下的充分条件来判断函数是否满足Lipschitz条件,即: 




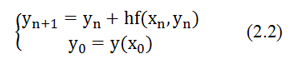 当然上面这个计算公式可以用三种方法得到,分别是:数值积分方法、Taylor展开方法、数值微分方法,即:
当然上面这个计算公式可以用三种方法得到,分别是:数值积分方法、Taylor展开方法、数值微分方法,即: 

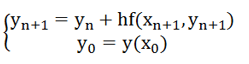


 上面的迭代公式中,第一步迭代还是需要用显式公式进行计算,后面的迭代采用隐式Euler法。很自然地,需要考虑上述迭代法的收敛性,即:
上面的迭代公式中,第一步迭代还是需要用显式公式进行计算,后面的迭代采用隐式Euler法。很自然地,需要考虑上述迭代法的收敛性,即: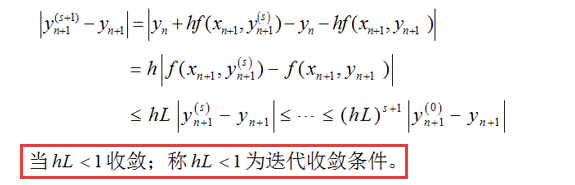
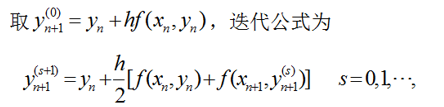


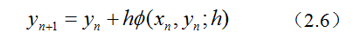 正如前述,其整体截断误差为通过
x
0
,
y
0
x_0,y_0
x0,y0,计算
y
1
,
y
2
,
.
.
.
,
y
n
y_1,y_2,...,y_n
y1,y2,...,yn,最后再计算整体截断误差
e
n
=
y
(
x
n
)
−
y
n
e_n=y(x_n)-y_n
en=y(xn)−yn,注意带括号的是精确值,带下标的是估计值,
正如前述,其整体截断误差为通过
x
0
,
y
0
x_0,y_0
x0,y0,计算
y
1
,
y
2
,
.
.
.
,
y
n
y_1,y_2,...,y_n
y1,y2,...,yn,最后再计算整体截断误差
e
n
=
y
(
x
n
)
−
y
n
e_n=y(x_n)-y_n
en=y(xn)−yn,注意带括号的是精确值,带下标的是估计值,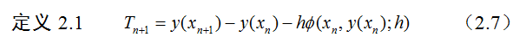


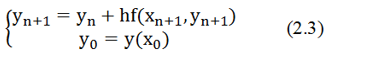 其局部截断误差表达式为:
其局部截断误差表达式为: