| 信号功率谱密度理解及其与频谱和能量谱的区别 | 您所在的位置:网站首页 › 怎么理解分布函数和密度函数的关系和区别和联系 › 信号功率谱密度理解及其与频谱和能量谱的区别 |
信号功率谱密度理解及其与频谱和能量谱的区别
|
信号功率谱密度理解及其与频谱和能量谱的区别
一、功率谱密度的特点
信号的功率谱密度函数是指这样的频率函数: (1)在整个频率范围内对它进行积分后,就能得到信号的总功率; (2)它描述了信号功率在各个不同频率上的分布的情况。 二、信号的平均功率一个随机过程的样本函数,尽管它的总能量是无限的,但是其平均功率却是有限值。假设 A ( t ) A(t) A(t)表示噪声电压,是一个随机过程; x ( t , ξ ) x(t,\xi) x(t,ξ)为随机过程 A ( t ) A(t) A(t)的样本函数,则噪声电压 x ( t , ξ ) x(t,\xi) x(t,ξ)在1Ω电阻上消耗的平均功率 W ξ W_ {\xi } Wξ,可由下式子计算: W ξ = lim T → ∞ 1 2 T ∫ − T T [ x ( t , ξ ) ] 2 d t (1) W_ {\xi } = \lim _ {T\rightarrow \infty } \frac {1}{2T} \int _ {-T}^ {T} [x(t,\xi) ]^ {2} dt \tag1 Wξ=T→∞lim2T1∫−TT[x(t,ξ)]2dt(1) 对于随机过程样本函数 x ( t , ξ ) x(t,\xi) x(t,ξ),研究其频谱没有很好的物理意义,研究其平均功率随频率的分布则具有更好的物理意义。 三、随机过程 A ( t ) A(t) A(t)的样本函数 x ( t , ξ ) x(t,\xi) x(t,ξ)的截断和其频谱函数将随机过程 A ( t ) A(t) A(t)的样本函数 x ( t , ξ ) x(t,\xi) x(t,ξ)任意截取一段,长度为 2 T 2T 2T,并记为 x T ( t , ξ ) x_{T}(t,\xi) xT(t,ξ),并称 x T ( t , ξ ) x_{T}(t,\xi) xT(t,ξ)为样本函数 x ( t , ξ ) x(t,\xi) x(t,ξ)的截断函数,如图1所示。
截断后,截断函数 x T ( t , ξ ) x_T(t,\xi) xT(t,ξ)其表达式为: x T ( t , ξ ) = { x ( t , ξ ) , ∣ t ∣ ≤ T 0 , ∣ t ∣ > T (2) {x_T}(t,\xi ) = \left\{ \begin{array}{l}x(t,\xi ),\quad |t| \le T\\0,\quad \quad \quad |t| > T\end{array} \right. \tag2 xT(t,ξ)={x(t,ξ),∣t∣≤T0,∣t∣>T(2) 对于有限连续时间的 x T ( t , ξ ) x_T(t,\xi) xT(t,ξ)而言,傅里叶变换是存在的,于是有: X T ( ω , ξ ) = ∫ − ∞ + ∞ x ( t , ξ ) e − j ω t d t = ∫ − T T x T ( t , ξ ) e − j ω t d t (3) {X_T}(\omega ,\xi ) = \int_{ - \infty }^{ + \infty } {x(t,\xi ){e^{ - j\omega t}}dt} \\ = \int_{ - T}^T {{x_T}(t,\xi ){e^{ - j\omega t}}dt} \tag3 XT(ω,ξ)=∫−∞+∞x(t,ξ)e−jωtdt=∫−TTxT(t,ξ)e−jωtdt(3) x T ( t , ξ ) = 1 2 π ∫ − ∞ + ∞ X T ( ω , ξ ) e j ω t d ω (4) {x_T}(t,\xi ) = \frac{1}{{2\pi }}\int_{ - \infty }^{ + \infty } {{X_T}(\omega ,\xi ){e^{j\omega t}}d\omega }\tag4 xT(t,ξ)=2π1∫−∞+∞XT(ω,ξ)ejωtdω(4) 其中 X T ( ω , ξ ) {X_T}(\omega ,\xi ) XT(ω,ξ)是 x T ( t , ξ ) {x_T}(t,\xi ) xT(t,ξ)的频谱函数。 四、功率谱密度推导若把式子(4)代入式子(1)来求解平均功率的另一种表示方式——频域表示方式。则计算过程如式子(5)所示。 W ξ = lim T → ∞ 1 2 T ∫ − T T [ x T ( t , ξ ) ] 2 d t W_{\xi} =\lim _{T \rightarrow \infty} \frac{1}{2 T} \int_{-T}^T\left[x_T(t, \xi)\right]^2 \mathrm{~d} t Wξ=T→∞lim2T1∫−TT[xT(t,ξ)]2 dt = lim T → ∞ 1 2 T ∫ − T T x T ( t , ξ ) [ 1 2 π ∫ − ∞ + ∞ X T ( ω , ξ ) e j ω t d ω ] d t =\lim _{T \rightarrow \infty} \frac{1}{2 T} \int_{-T}^T x_T(t, \xi)\left[\frac{1}{2 \pi} \int_{-\infty}^{+\infty} X_T(\omega, \xi) \mathrm{e}^{\mathrm{j} \omega t} \mathrm{~d} \omega\right] \mathrm{d} t \\ =T→∞lim2T1∫−TTxT(t,ξ)[2π1∫−∞+∞XT(ω,ξ)ejωt dω]dt = lim T → ∞ 1 2 T ∫ − T T 1 2 π X T ( ω , ξ ) [ ∫ − T T x T ( t , ξ ) e j ω t d t ] d ω =\lim _{T \rightarrow \infty} \frac{1}{2 T} \int_{-T}^T \frac{1}{2 \pi} X_T(\omega, \xi)\left[\int_{-T}^T x_T(t, \xi) \mathrm{e}^{\mathrm{j} \omega t} \mathrm{~d} t\right] \mathrm{d} \omega =T→∞lim2T1∫−TT2π1XT(ω,ξ)[∫−TTxT(t,ξ)ejωt dt]dω = 1 2 π lim T → ∞ 1 2 T ∫ − T T X T ( ω , ξ ) [ ∫ − T T x T ( t , ξ ) e − j ω t ‾ d t ] d ω = \frac{1}{{2\pi }} {\lim_{T \rightarrow \infty }} \frac{1}{{2T}}\int_{ - T}^T {{X_T}(\omega ,\xi )\left[ {\int_{ - T}^T {{x_T}(t,\xi )\overline {{{\rm{e}}^{{\rm{ - j}}\omega t}}} } \;{\rm{d}}t} \right]} {\rm{d}}\omega =2π1T→∞lim2T1∫−TTXT(ω,ξ)[∫−TTxT(t,ξ)e−jωtdt]dω = 1 2 π lim T → ∞ 1 2 T ∫ − T T X T ( ω , ξ ) [ ∫ − T T x T ( t , ξ ) ‾ e − j ω t ‾ d t ] d ω = \frac{1}{{2\pi }} {\lim_{T \to \infty }} \frac{1}{{2T}}\int_{ - T}^T {{X_T}(\omega ,\xi )} \left[ {\int_{ - T}^T {\overline {\overline {{x_T}(t,\xi )} {{\rm{e}}^{{\rm{ - j}}\omega t}}} } \;{\rm{d}}t} \right]{\rm{d}}\omega =2π1T→∞lim2T1∫−TTXT(ω,ξ)[∫−TTxT(t,ξ)e−jωtdt]dω = 1 2 π lim T → ∞ 1 2 T ∫ − T T X T ( ω , ξ ) [ ∫ − T T x T ( t , ξ ) ‾ e − j ω t d t ‾ ] d ω (5) = \frac{1}{{2\pi }} {\lim_{T \to \infty } } \frac{1}{{2T}}\int_{ - T}^T {{X_T}(\omega ,\xi )} \left[ {\overline {\int_{ - T}^T {\overline {{x_T}(t,\xi )} {{\rm{e}}^{{\rm{ - j}}\omega t}}{\rm{d}}t} } \;} \right]{\rm{d}}\omega \tag5 =2π1T→∞lim2T1∫−TTXT(ω,ξ)[∫−TTxT(t,ξ)e−jωtdt]dω(5) 又因为 x T ( t , ξ ) x_T(t, \xi) xT(t,ξ)为实函数,则 x T ( t , ξ ) = x T ( t , ξ ) ‾ x_T(t, \xi)=\overline{x_T(t, \xi)} xT(t,ξ)=xT(t,ξ),那么式子(5)进一步可计算 W ξ = lim T → ∞ 1 2 T ∫ − T T [ x T ( t , ξ ) ] 2 d t W_{\xi} =\lim _{T \rightarrow \infty} \frac{1}{2 T} \int_{-T}^T\left[x_T(t, \xi)\right]^2 \mathrm{~d} t Wξ=T→∞lim2T1∫−TT[xT(t,ξ)]2 dt = 1 2 π lim T → ∞ 1 2 T ∫ − T T X T ( ω , ξ ) [ ∫ − T T x T ( t , ξ ) ‾ e − j ω t ‾ d t ] d ω = \frac{1}{{2\pi }} {\lim_{T \to \infty }} \frac{1}{{2T}}\int_{ - T}^T {{X_T}(\omega ,\xi )} \left[ {\int_{ - T}^T {\overline {\overline {{x_T}(t,\xi )} {{\rm{e}}^{{\rm{ - j}}\omega t}}} } \;{\rm{d}}t} \right]{\rm{d}}\omega =2π1T→∞lim2T1∫−TTXT(ω,ξ)[∫−TTxT(t,ξ)e−jωtdt]dω = 1 2 π lim T → ∞ 1 2 T ∫ − T T X T ( ω , ξ ) [ ∫ − T T x T ( t , ξ ) e − j ω t d t ‾ ] d ω = \frac{1}{{2\pi }} {\lim _{T \to \infty }} \frac{1}{{2T}}\int_{ - T}^T {{X_T}(\omega ,\xi )} \left[ {\overline {\int_{ - T}^T {{x_T}(t,\xi ){{\rm{e}}^{{\rm{ - j}}\omega t}}{\rm{d}}t} } \;} \right]{\rm{d}}\omega =2π1T→∞lim2T1∫−TTXT(ω,ξ)[∫−TTxT(t,ξ)e−jωtdt]dω = 1 2 π lim T → ∞ 1 2 T ∫ − T T X T ( ω , ξ ) X T ( ω , ξ ) ‾ d ω = \frac{1}{{2\pi }} {\lim_{T \to \infty } } \frac{1}{{2T}}\int_{ - T}^T {{X_T}(\omega ,\xi )} \overline {{X_T}(\omega ,\xi )} {\rm{d}}\omega =2π1T→∞lim2T1∫−TTXT(ω,ξ)XT(ω,ξ)dω = 1 2 π lim T → ∞ 1 2 T ∫ − T T ∣ X T ( ω , ξ ) ∣ 2 d ω = \frac{1}{{2\pi }} {\lim_{T \to \infty } } \frac{1}{{2T}}\int_{ - T}^T {|{X_T}(\omega ,\xi ){|^2}} {\rm{d}}\omega =2π1T→∞lim2T1∫−TT∣XT(ω,ξ)∣2dω = 1 2 π ∫ − ∞ + ∞ lim T → ∞ 1 2 T ∣ X T ( ω , ξ ) ∣ 2 d ω (6) = \frac{1}{{2\pi }}\int_{ - \infty }^{ + \infty } { {\lim_{T \to \infty } }\ \frac{1}{{2T}}|{X_T}(\omega ,\xi ){|^2}} {\rm{d}}\omega \tag6 =2π1∫−∞+∞T→∞lim 2T1∣XT(ω,ξ)∣2dω(6) 式(6)中的被积函数 lim T → ∞ 1 2 T ∣ X T ( ω , ξ ) ∣ 2 \lim_{T \to \infty}\frac{1}{2T}|{X_T}(\omega ,\xi ) |^2 T→∞lim2T1∣XT(ω,ξ)∣2具备功率谱密度的特点,它代表了随机过程的某一个样本函数 x ( t , ξ ) x(t,\xi) x(t,ξ)在频域中 ω \omega ω频率处,消耗在1Ω电阻上的平均功率。因此,称它为样本函数 x ( t , ξ ) x(t,\xi) x(t,ξ)的功率谱密度函数,记作 G ( ω , ξ ) G(\omega ,\xi ) G(ω,ξ). G ( ω , ξ ) = lim T → ∞ 1 2 T ∣ X T ( ω , ξ ) ∣ 2 (7) G(\omega ,\xi )=\lim_{T \to \infty}\frac{1}{2T}|{X_T}(\omega ,\xi ) |^2 \tag7 G(ω,ξ)=T→∞lim2T1∣XT(ω,ξ)∣2(7) 五、功率谱密度函数与能量谱密度函数以及频谱的区别(1)频谱、能量谱以及功率谱是三个不同的概念,要特别注意区分,不能混淆三者概念。 (2)频谱函数是经过傅里叶变换直接得到的,即 X ( ω , ξ ) = ∫ − ∞ + ∞ x ( t , ξ ) e − j ω t d t (8) {X}(\omega ,\xi ) = \int_{ - \infty }^{ + \infty } {x(t,\xi ){e^{ - j\omega t}}dt} \tag8 X(ω,ξ)=∫−∞+∞x(t,ξ)e−jωtdt(8) 能量谱由频谱取模再平方得到,即 S ( ω , ξ ) = ∣ X T ( ω , ξ ) ∣ 2 (9) S(\omega ,\xi ) =|{X_T}(\omega ,\xi ) |^2 \tag9 S(ω,ξ)=∣XT(ω,ξ)∣2(9) 而功率谱,是能量谱结合时间因素而得到的: G ( ω , ξ ) = lim T → ∞ 1 2 T ∣ X T ( ω , ξ ) ∣ 2 (7) G(\omega ,\xi ) =\lim_{T \to \infty}\frac{1}{2T}|{X_T}(\omega ,\xi ) |^2 \tag7 G(ω,ξ)=T→∞lim2T1∣XT(ω,ξ)∣2(7) |
【本文地址】
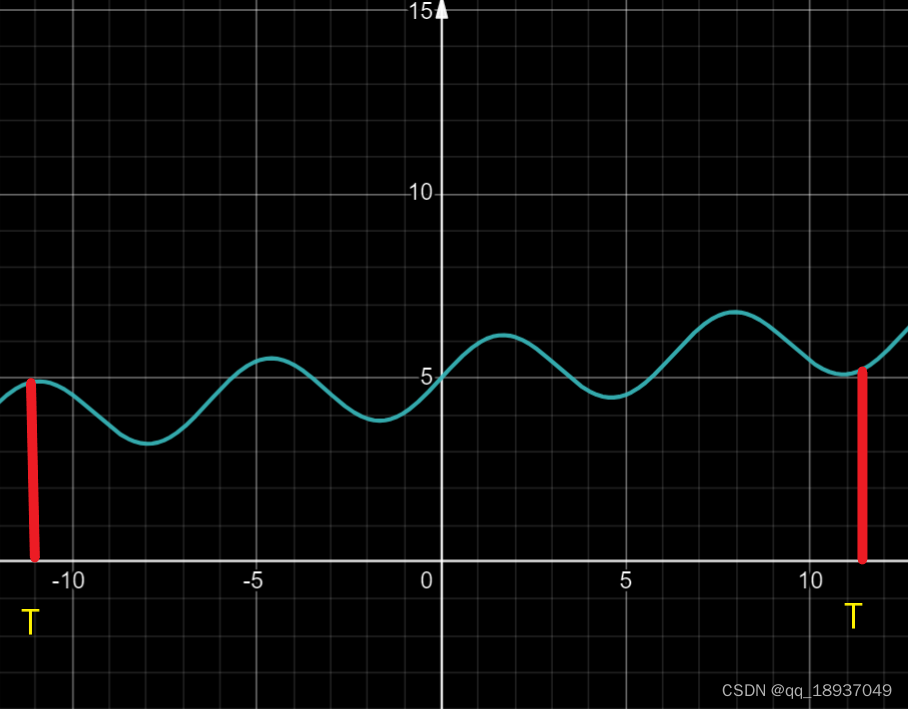 图1 样本函数的截断函数
x
T
(
t
,
ξ
)
x_T(t,\xi)
xT(t,ξ)
图1 样本函数的截断函数
x
T
(
t
,
ξ
)
x_T(t,\xi)
xT(t,ξ)