线性代数

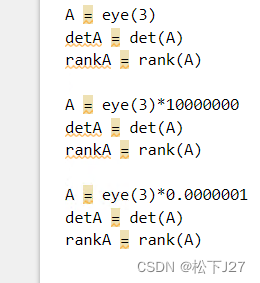
        一般情况下，判断矩阵是否可逆大多数人都会选择计算矩阵的行列式（determinant）？如果矩阵的行列式为0，则判断该矩阵为奇异矩阵（singular matrix），即不可逆矩阵。而如果该矩阵的行列式不为0，则判断该矩阵为非奇异矩阵（nonsingular matrix）。

以3x3的单位矩阵为例

Matlab code:

 Result:

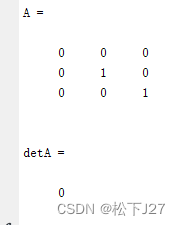
        现在我们略微改变一下这个矩阵，把原单位阵中的第一个值改成0，则该矩阵不可逆，且行列式的值为0：

Matlab code:

Result:

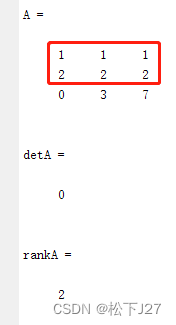
        事实上，所谓不可逆/奇异矩阵就是“特殊”或“奇怪”的意思，所以英文中用singular来表示。其实，矩阵是否可逆的本质就是矩阵中的各列/各行是否线性相关，只要线性相关，肯定不可逆。

下面我用matlab来测试一下：

行相关矩阵

Matlab code:

Result:

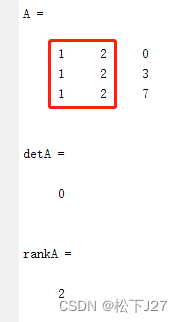
矩阵A的第一行和第二行相关，矩阵不可逆，矩阵的秩为2，不满秩(满秩为3)。

列相关矩阵 

Matlab code:

 Result:

矩阵A的第一列和第二列相关，矩阵不可逆，矩阵的秩为2，不满秩(满秩为3)。

        如果矩阵为奇异矩阵，不可逆，则方程组Ax=0有平凡解以外的解。方程组Ax=b无解，或者有无穷多个解。

如果矩阵为非奇异矩阵，可逆，则方程组Ax=0仅有平凡解，Ax=b有唯一解。

看看下面这个例子：

        还是前面的3x3单位矩阵（单位矩阵是经典的可逆矩阵，他的行与行，列与列之间都是线性无关的，更准备的说，单位矩阵的每一行或者每一列都是用于张成子空间的基底向量），但这次我们让这个单位矩阵分别乘以一个特别大和特别小的正数c*A，然后再来重新计算矩阵的行列式，看看他们是否依然可以通过行列式的值来判断是否可逆？

        理论上讲，单位矩阵的倍数cA，经过高斯消元后，一定还是单位矩阵，也就是绝对可逆，行列式的值一定不为0。下面我们看看计算结果：

Matlab code:

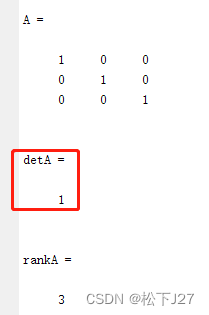
Result:

        这是标准单位矩阵的计算结果，矩阵的秩等于3，满秩。矩阵的行列式不等于0，这些都说明了该矩阵可逆，不是奇异矩阵。

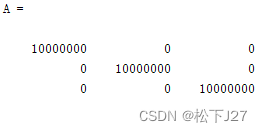
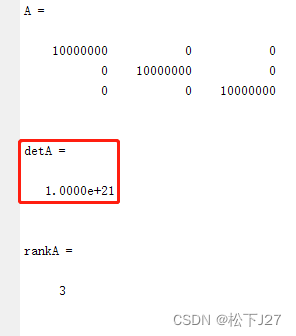
         矩阵乘以1000000后，依然可逆。秩等于3，满秩。行列式的值很大，不等于0，说明矩阵可逆。

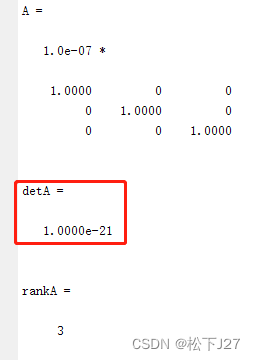
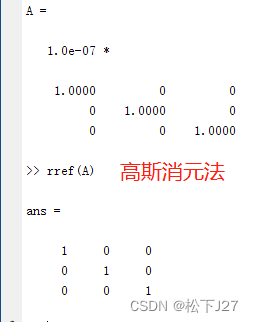
         这是乘以0.0000001后的矩阵，他不是奇异矩阵，因为他是单位矩阵的倍数。同样，该矩阵满秩。且，矩阵的行列式不等于0。

        现在问题来了，在大多数情况下，不论是手动计算行列式，还是计算机运算行列式，都很难得到一个精确的“0”。事实上，人们会定义一个特别小的值TINY，例如TINY=1xe-15次方，并把这个TINY等同于0。当一个矩阵的行列式的计算结果非常小，且小于TINY时，即接近于0时，则我们认定，该矩阵为奇异矩阵。

        可事实证明并非如此，通过我们上面的三个矩阵的比对结果发现，如果用TINY做为0的方法来判断矩阵是否可逆，则最后一个矩阵（也就是用一个很小的数乘以单位矩阵的结果）一定会被判定为奇异矩阵，即不可逆矩阵。可该矩阵正好是各列，各行都完全线性无关，是一个标标准准，如假包换的可逆矩阵。

        换句话说，当我们把行列式的值是否为0，作为判断矩阵是否可逆的金标准时。又因为，种种原因，导致我们在判断行列式是否为0时，不得不设置一个很小的值TINY，作为判断标准。继而，给人一种误解，那就是：“行列式的值“似乎”越小/越接近于0，则矩阵越有可能是奇异矩阵，越有可能不可逆。”

        但实际上，本例中的三个单位矩阵的实验告诉我们，事实上通过高斯消元，他们其实就是同一个矩阵，但他们的行列式却千差万别。

        这时，我们就要用到另外一个判断矩阵是否可逆的方法，条件数(condition number)：在Matlab的算法中，条件数接近 1 则表示该矩阵为良态矩阵(即可逆矩阵），而条件数越大则说明该矩阵越有可能是病态矩阵(趋向于不可逆矩阵)，当条件数接近无穷大时Inf时，该矩阵为奇异矩阵(不可逆矩阵)。他在判断矩阵是否可逆方面，比矩阵的行列式更加准确，也更加稳定，当然，最好的办法还是结合行列式和条件数一同使用。

Matlab code:

 Result: 

        三个矩阵的计算结果都是1，根据用条件数判定矩阵是否可逆的原则，矩阵的条件数接近1，表示该矩阵为可逆矩阵。

此外，我这里也写过一篇专门介绍条件数的文章，有兴趣的朋友可以看看：

     线性代数 --- 用条件数(condition number)来判断矩阵是否可逆_松下J27的博客-CSDN博客_matlab中判断矩阵是否可逆​现在我们介绍一种全新的判断矩阵是否可逆的方法，英文叫condition number，中文翻译为条件数。这也是我在matlab里面看到的一个方法，在matlab中的命令为cond(A)。它是方程组Ax=b中右端b的变换对于解x的影响的一个度量值，用希腊字母表示。​https://blog.csdn.net/daduzimama/article/details/120494425

（下图为早些时候的学习笔记）

（全文完）

作者 --- 松下J27

格言摘抄：

施比受更为有福。--- 徒20:35

参考文献（鸣谢）：

1, 矩阵行列式 - MATLAB det- MathWorks 中国

2,逆运算的条件数 - MATLAB cond- MathWorks 中国

（配图与本文无关） 

版权声明：所有的笔记，可能来自很多不同的网站和说明，在此没法一一列出，如有侵权，请告知，立即删除。欢迎大家转载，但是，如果有人引用或者COPY我的文章，必须在你的文章中注明你所使用的图片或者文字来自于我的文章，否则，侵权必究。 ----松下J27