| 快速幂实现pow函数(从二分和二进制两种角度理解快速幂) | 您所在的位置:网站首页 › 幂函数x的-2次方的图像 › 快速幂实现pow函数(从二分和二进制两种角度理解快速幂) |
快速幂实现pow函数(从二分和二进制两种角度理解快速幂)
|
文章目录
迭代实现快速幂思路int的取值范围快速幂从二进制的角度来理解从二分法的角度来理解
代码复杂度分析
进阶——超级次方思路倒序+快速幂正序+快速幂
代码复杂度分析
迭代实现快速幂
实现 pow(x, n) ,即计算 x 的 n 次幂函数(即,xn)。不得使用库函数,同时不需要考虑大数问题。 示例 1: 输入:x = 2.00000, n = 10 输出:1024.00000 示例 2: 输入:x = 2.10000, n = 3 输出:9.26100 示例 3: 输入:x = 2.00000, n = -2 输出:0.25000 解释:2-2 = 1/22 = 1/4 = 0.25 提示: -100.0 < x < 100.0 -231 if(x == 0) return 0; double sum = 1; long long m = n; if(n if(m & 1){ sum *= x; } x *= x; m >>= 1; } return sum; } }; 复杂度分析 时间复杂度 O(log_2 n): 二分的时间复杂度为对数级别。空间复杂度 O(1): sum, b 等变量占用常数大小额外空间。 进阶——超级次方 计算 ab 对 1337 取模,a 是一个正整数,b 是一个非常大的正整数且会以数组形式给出。 思路本题的难点在于对 数组b 的处理,显然无法将其转为 一个具体类型,因此解决方法无非就是 在 倒序 or 正序 遍历数组的同时进行次方处理。 倒序+快速幂本质无非就是把上面提到的二进制思想转为十进制,具体来说: 223 可以看作 2(10 * 2) + (1 * 3) ,也就是 10242 * 23 。 那么我们只需要在第 k 次 倒序遍历 数组 b 的同时,记录 a 的 10k-1 次方即可。 正序+快速幂思路源于秦九韶算法,一般地,一元 n 次多项式的求值需要经过 ( n + 1 ) ∗ n 2 \frac{(n+1)*n}{2} 2(n+1)∗n 次乘法和 n n n 次加法,而秦九韶算法只需要 n n n 次乘法和 n n n 次加法。大大简化了运算过程。 把一个 n 次多项式: 举个具体的例子,计算 2 234 2^{234} 2234: 2 234 = 2 200 + 30 + 4 = 2 200 ∗ 2 30 ∗ 2 4 = ( 2 20 ∗ 2 3 ) 10 ∗ 2 4 = [ ( 1 10 ∗ 2 2 ) 10 ∗ 2 3 ] 10 ∗ 2 4 2^{234} = 2^{200+30+4} = 2^{200} * 2^{30} * 2^4 = (2^{20} * 2^3)^{10} * 2^4 = [(1^{10} * 2^2)^{10} * 2^3]^{10} * 2^4 2234=2200+30+4=2200∗230∗24=(220∗23)10∗24=[(110∗22)10∗23]10∗24 最后一步推导实际上是对规律的归纳,即:以 1 作为初始值 res,每次有 新项 加入时,对 res 执行 r e s = r e s 10 ∗ 新 项 res = res^{10} * 新项 res=res10∗新项 的操作。 代码 class Solution { const int MOD = 1337; int quickmul(int x, int n){ // 快速幂实现pow功能 if(x == 0) return 0; int sum = 1; while(n){ if(n&1) sum = (long)sum * x % MOD; n >>= 1; x = (long)x * x % MOD; } return sum; } public: int superPow(int a, vector& b) { // 倒序 int res = 1, n = b.size(); for(int i=n-1; i>=0; i--){ res = (long)res * quickmul(a, b[i]) % MOD; a = quickmul(a, 10); // 记录当前 a 的幂 } return res; } int superPow(int a, vector& b) { // 正序 int res = 1, n = b.size(); for(int i : b){ res = (long)quickmul(res, 10) * quickmul(a, i) % MOD; // 加入新项时,对 res 执行 res = res^10 * 新项 的操作 } return res; } }; 复杂度分析 时间复杂度O( ∑ i = 0 n − 1 log b i \sum_{i=0}^{n-1}{\log{b_i}} ∑i=0n−1logbi): 其中 n 是数组 b 的长度,对每个 b i b_i bi 计算快速幂的时间为 O( log b i \log{b_i} logbi)。空间复杂度O(1): 过程由迭代实现,避免了递归方法对栈空间的占用,只需要常数的空间存放若干变量。 |
【本文地址】
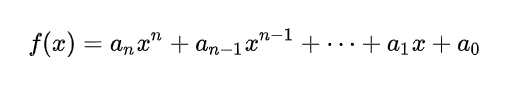 改写成如下形式:
改写成如下形式: 