[含Matlab程序]最小二乘法线性（以空间平面为例）与非线性（以二次函数为例）拟合，不看后悔

最小二乘法解决的是什么问题？使用最小二乘法求参数的关键是什么？ ○最小二乘法用于处理数据拟合问题，本质是实现向量向 X {\rm X} X矩阵的列空间投影 ○关键是找 X {\rm X} X矩阵

做两个假设 1.我们手中有m个散点，要想用一条直线去拟合，散点的形式是： X = [ x 0 x 1 ⋮ x m − 1 ] Y = [ y 0 y 1 ⋮ y m − 1 ] X = {\begin{bmatrix} {{x_0}}\\ {{x_1}}\\ \vdots \\ {{x_{m - 1}}} \end{bmatrix}} Y = {\begin{bmatrix} {{y_0}}\\ {{y_1}}\\ \vdots \\ {{y_{m - 1}}} \end{bmatrix}} X= ​x0​x1​⋮xm−1​​ ​Y= ​y0​y1​⋮ym−1​​ ​

2.假如这条直线的形式是已知的，如下： h = θ 0 x + θ 1 h = {\theta _0}x+{\theta _1} h=θ0​x+θ1​

将我们已知的点的自变量x代入，可以得到以下形式，因此由这条拟合直线可以给我们输出m个结果组成向量H：

h 0 = θ 0 x 0 + θ 1 h 1 = θ 0 x 1 + θ 1 ⋮ h m − 1 = θ 0 x m − 1 + θ 1 \begin{array}{l} {h_0} = {\theta _0}{x_0} + {\theta _1}\\ {h_1} = {\theta _0}{x_1} + {\theta _1}\\ \vdots \\ {h_{m-1}} = {\theta _0}{x_{m-1}} + {\theta _1} \end{array} h0​=θ0​x0​+θ1​h1​=θ0​x1​+θ1​⋮hm−1​=θ0​xm−1​+θ1​​ H = [ h 0 h 1 ⋮ h m − 1 ] = [ x 0 1 x 1 1 ⋮ ⋮ x m − 1 1 ] [ θ 0 θ 1 ] = X θ (1) {H}= \begin{bmatrix} h_0 \\ h_1 \\ \vdots \\ h_{m-1} \\ \end{bmatrix}=\begin{bmatrix} x_0 &1\\ x_1 &1\\ \vdots &\vdots\\ x_{m-1} &1\\ \end{bmatrix}\begin{bmatrix} \theta_0 \\ \theta_1 \\ \end{bmatrix}={\rm X}{\theta}\tag{1} H= ​h0​h1​⋮hm−1​​ ​= ​x0​x1​⋮xm−1​​11⋮1​ ​[θ0​θ1​​]=Xθ(1) 注意这个 X {\rm X} X从原来的 X X X向量的基础上扩展成mx2的矩阵。 用下面这个公式描述直线的输出值和真实散点的y值的差距：

J ( θ ) = ∥ H − Y ∥ 2 = ∥ H − Y ∥ 2 = ∥ X θ − Y ∥ 2 J(\theta) = {\left\| {H - Y} \right\|^2} = {\left\| {H - Y} \right\|^2} = {\left\| {{\rm X}\theta - Y} \right\|^2} J(θ)=∥H−Y∥2=∥H−Y∥2=∥Xθ−Y∥2 最小二乘法的目的就在于实现解出 θ \theta θ矩阵，使 J ( θ ) J(\theta ) J(θ)最小化，即： arg ⁡ min ⁡ θ J ( θ ) \mathop {\arg \min }\limits_\theta J(\theta ) θargmin​J(θ) 具体是通过矩阵求导实现解出 θ \theta θ矩阵的，参考这篇文章：一文让你彻底搞懂最小二乘法（超详细推导） 这里直接给出结果： θ = ( X T X ) − 1 X T Y (2) \theta = {({{\rm X}^T}{\rm X})^{ - 1}}{{\rm X}^T}Y\tag{2} θ=(XTX)−1XTY(2) 这个形式让人联想起投影矩阵。 H = X θ = X ( X T X ) − 1 X T Y = P Y H = {\rm X}\theta ={\rm X}{({{\rm X}^T}{\rm X})^{ - 1}}{{\rm X}^T}Y={P}Y H=Xθ=X(XTX)−1XTY=PY 其中的P就是常说的投影矩阵，即： P = X ( X T X ) − 1 X T P={\rm X}{({{\rm X}^T}{\rm X})^{ - 1}}{{\rm X}^T} P=X(XTX)−1XT 从形式上看，拟合的输出向量 H H H实际上是真实散点的因变量（对于直线来说就是 Y Y Y）向量向自变量 X {\rm X} X矩阵的列空间投影的结果。 对于直线而言， X {\rm X} X的列空间就是由下面两个向量张成的空间： [ x 0 x 1 ⋮ x m − 1 ] 和 [ 1 1 ⋮ 1 ] \begin{bmatrix} x_0 \\ x_1 \\ \vdots \\ x_{m-1} \\ \end{bmatrix}和\begin{bmatrix} 1 \\ 1 \\ \vdots \\ 1 \\ \end{bmatrix} ​x0​x1​⋮xm−1​​ ​和 ​11⋮1​ ​

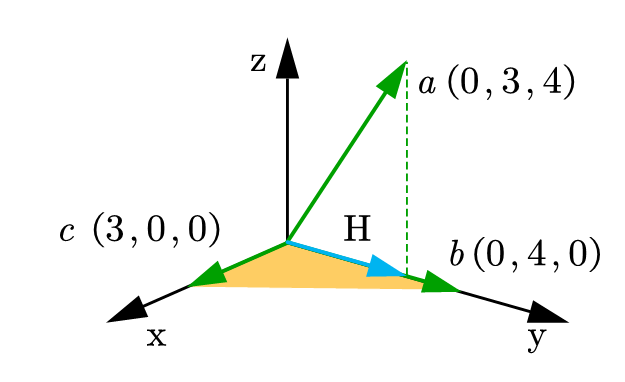
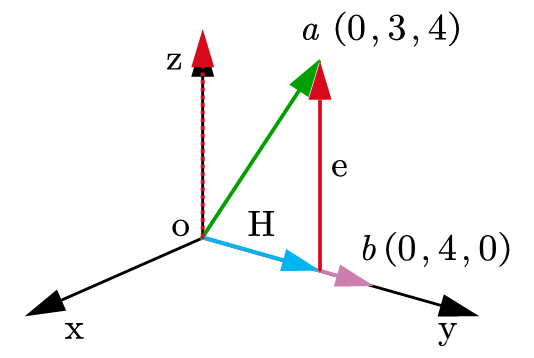
向量的投影可以用来对向量进行正交化。 矩阵的投影则可以把向量投影到空间。 线性代数（十三）投影 对于矩阵 [ 3 0 0 4 0 0 ] \begin{bmatrix} 3&0 \\ 0&4 \\ 0&0 \\ \end{bmatrix} ​300​040​ ​ 张成的空间，在下图中即是由向量 c c c和向量 b b b张成的黄色平面。图上标注的是一个三角，实际是一个平面，这个平面中的向量都可以用向量 c c c和向量 b b b线性组合的形式表达。

如果向量 a a a要向这个平面投影，根据投影矩阵：

H = X ( X T X ) − 1 X T Y = P Y H ={\rm X}{({{\rm X}^T}{\rm X})^{ - 1}}{{\rm X}^T}Y={P}Y H=X(XTX)−1XTY=PY 在本题中： Y = [ 0 3 4 ] X = [ 3 0 0 4 0 0 ] Y=\begin{bmatrix} 0 \\ 3 \\ 4\\ \end{bmatrix} {\rm X}=\begin{bmatrix} 3&0\\ 0&4 \\ 0&0\\ \end{bmatrix} Y= ​034​ ​X= ​300​040​ ​ 因此可以求出投影到 X {\rm X} X张成平面上的结果是: H = [ 0 3 0 ] H=\begin{bmatrix} 0\\ 3\\ 0\\ \end{bmatrix} H= ​030​ ​ 用这样一段程序（matlab）就能快速计算：

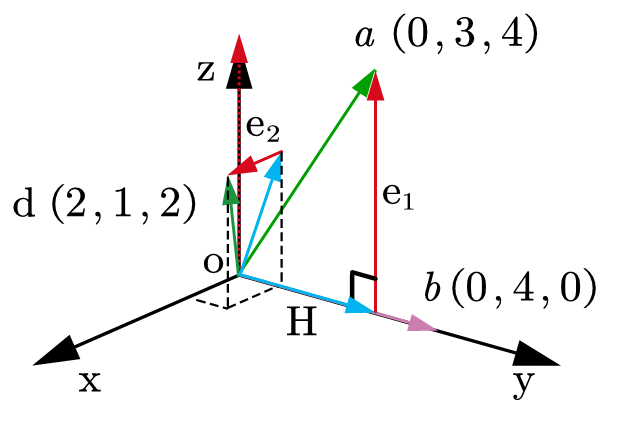
在这里顺势介绍一下向量的正交化，这块和最小二乘法关系不大但是和投影关系比较大。 如下图，向量 a a a和向量 b b b原本不是正交的（正交要求内积为0）， H H H是 a a a在 b b b上的投影，上一步我们已经求得，而 e = a − H e=a-H e=a−H且与 b b b是正交的， e e e很好求得，由于向量是可以平移的，把红色的 e e e向量的尾巴平移到原点处，就可以得到过原点的一个和 b b b正交的向量，这是对 a a a的正交化。

如果引入一个新的向量 d d d，要想使 d d d与正交化 a a a得到的 e 1 e_1 e1​以及 b b b都正交，要先作出 d d d到 e 1 e_1 e1​与 b b b张成平面的投影（下图中是一个蓝色的向量，没有字母标注），再用 d d d减去这个投影得到的向量就可以解出向量 e 2 e_2 e2​。最终 e 1 e 2 e_1e_2 e1​e2​和 b b b线性无关且两两正交。这三个向量分别除以各自的模长就得到两两正交的单位向量，这个操作也就是常说的单位化。

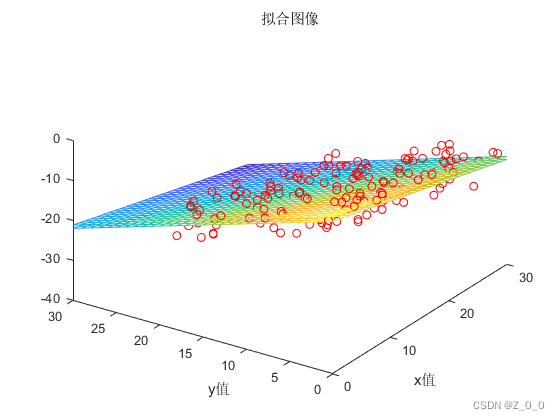
图片是本文原创，使用请标明出处。

注意平面环节中的符号和第一部分的直线环节的可能有相似之处，但意义不相同。 用不同的形式拟合散点，关键是构建 X {\rm X} X矩阵，对于平面， X {\rm X} X矩阵和直线是不同的。 平面的形式如下： a x + b y + c z + d = 0 或者用一个和直线环节介绍的类似的形式： h = θ 0 x 0 + θ 1 x 1 + θ 2 \begin{array}{l} ax + by +cz+d=0\\ \\ 或者用一个和直线环节介绍的类似的形式：\\ \\ h = {\theta _0}{x_0} + {\theta _1}{x_1} + {\theta _2} \end{array} ax+by+cz+d=0或者用一个和直线环节介绍的类似的形式：h=θ0​x0​+θ1​x1​+θ2​​ 可以看出如果找到一个平面去拟合散点，这个平面的因变量变成两个自变量线性组合的形式，而对于直线只有一个因变量。两个自变量 x 0 {x_0} x0​， x 1 {x_1} x1​分别对应着平面一般式中的 x x x和 y y y，而因变量 h h h则代表着一般式中的 z z z。 如果这时候我们手中有很多散点，把他们带入到平面方程中： h 0 = θ 0 x 0 , 0 + θ 1 x 0 , 1 + θ 2 h 1 = θ 0 x 1 , 0 + θ 1 x 1 , 1 + θ 2 ⋮ h m − 1 = θ 0 x m − 1 , 0 + θ 1 x m − 1 , 1 + θ 2 \begin{array}{l} {{h_0} = {\theta _0}{x_{0,0}} + {\theta _1}{x_{0,1}} + {\theta _2}}\\ {{h_1} = {\theta _0}{x_{1,0}} + {\theta _1}{x_{1,1}} + {\theta _2}}\\ \vdots \\ {{h_{m - 1}} = {\theta _0}{x_{m - 1,0}} + {\theta _1}{x_{m - 1,1}} + {\theta _2}} \end{array} h0​=θ0​x0,0​+θ1​x0,1​+θ2​h1​=θ0​x1,0​+θ1​x1,1​+θ2​⋮hm−1​=θ0​xm−1,0​+θ1​xm−1,1​+θ2​​

待求的参数是 θ 0 {\theta _0} θ0​， θ 1 {\theta _1} θ1​， θ 2 {\theta _2} θ2​，同样可以写成 H = X θ H={\rm X}{\theta} H=Xθ的形式，对于求解平面的这三个参数来说， X {\rm X} X矩阵是长得这个样子: [ x 0 , 0 x 0 , 1 1 x 1 , 0 x 1 , 1 1 ⋮ ⋮ ⋮ x m − 1 , 0 x m − 1 , 1 1 ] \begin{bmatrix} x_{0,0} &x_{0,1}&1\\ x_{1,0} &x_{1,1}&1\\ \vdots &\vdots &\vdots\\ x_{m-1,0} &x_{m-1,1}&1\\ \end{bmatrix} ​x0,0​x1,0​⋮xm−1,0​​x0,1​x1,1​⋮xm−1,1​​11⋮1​ ​ 而 Y {Y} Y矩阵就是我们手中散点的因变量，对于平面来说就是 z z z值，注意区分符号。 现在 X {\rm X} X和 Y {Y} Y矩阵都是已知的，根据 ( 2 ) (2) (2)式即可求解出 θ {\theta} θ矩阵（其实是向量）: [ θ 0 θ 1 θ 2 ] \begin{bmatrix} \theta_0 \\ \theta_1 \\ \theta_2 \\ \end{bmatrix} ​θ0​θ1​θ2​​ ​

假如手中一些散点，要用二次函数进行拟合，一个二次函数的典型形式如下： h = θ 0 x 2 + θ 1 x + θ 2 h = {\theta _0}x^2+{\theta _1} x+{\theta _2} h=θ0​x2+θ1​x+θ2​ 对于非线性的场景，关键仍然是找 X {\rm X} X矩阵，首先还是考虑怎么写成 ( 1 ) (1) (1)式的形式： H = [ h 0 h 1 ⋮ h m − 1 ] = [ x 0 2 x 0 1 x 1 2 x 1 1 ⋮ ⋮ ⋮ x m − 1 2 x m − 1 1 ] [ θ 0 θ 1 θ 2 ] = X θ {H}= \begin{bmatrix} h_0 \\ h_1 \\ \vdots \\ h_{m-1} \\ \end{bmatrix}=\begin{bmatrix} x_0^2 &x_0&1\\ x_1^2 &x_1&1\\ \vdots &\vdots&\vdots\\ x_{m-1}^2 &x_{m-1}&1\\ \end{bmatrix}\begin{bmatrix} \theta_0 \\ \theta_1 \\ \theta_2 \\ \end{bmatrix}={\rm X}{\theta} H= ​h0​h1​⋮hm−1​​ ​= ​x02​x12​⋮xm−12​​x0​x1​⋮xm−1​​11⋮1​ ​ ​θ0​θ1​θ2​​ ​=Xθ 对于更高次幂的函数，也是如此找 X {\rm X} X矩阵，因为对差距函数（损失函数） J ( θ ) J(\theta) J(θ)求导并使导函数等于零，这是一个对 θ \theta θ求导的过程，不管是线性还是非线性，结果都是 ( 2 ) (2) (2)式，因此只要找到 X {\rm X} X矩阵，就可以求出 θ {\theta} θ。

下面是matlab程序，首先介绍我自定义的LS_fit函数

LS_fit(自变量1,自变量2,因变量,是否是非线性,如果是非线性函数的话最高次项是几次)

新建一个脚本，调用刚才定义的LS_fit函数，首先展示平面拟合功能

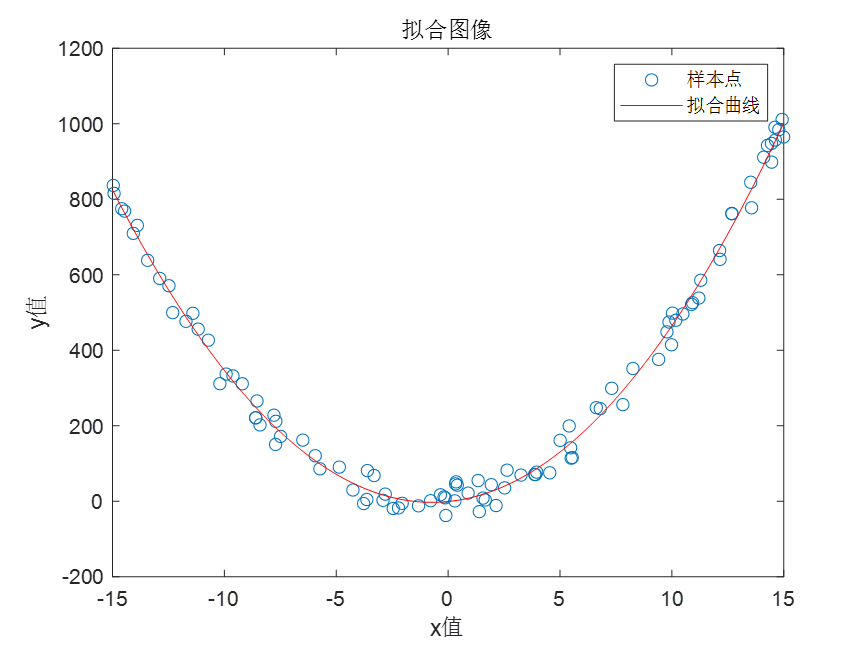
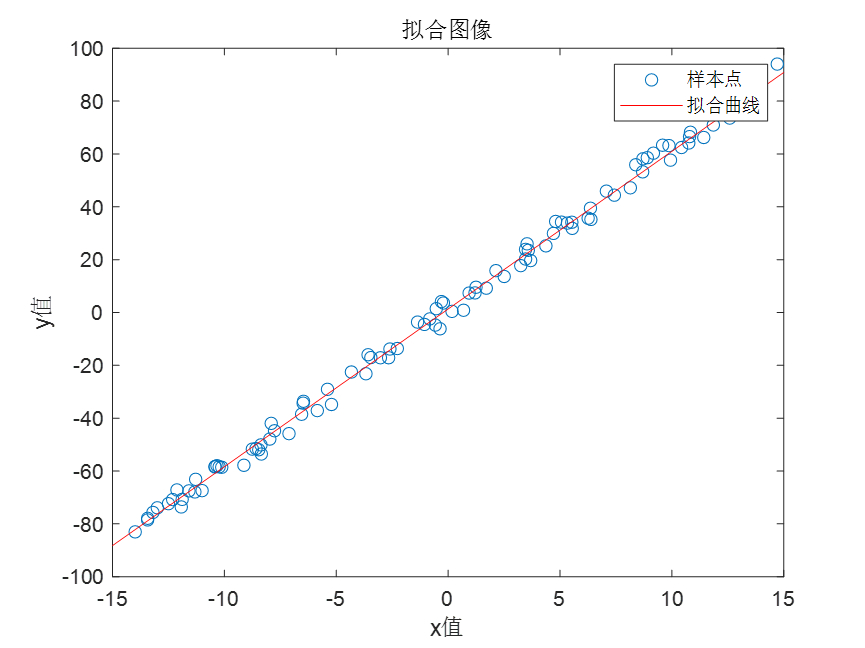
对于非线性的情况，以二次函数拟合为例，程序如下：

拟合的结果：

注意：即使是使用的函数的非线性模式，也可以解决一次函数拟合的问题，也就是一次函数是一种特殊的非线性函数。

针对 h = θ 0 e θ 1 x h = {\theta _0}{{\rm{e}}^{{\theta _1}x}} h=θ0​eθ1​x的形式，首先线性化，两边取对数可得 ln ⁡ h = ln ⁡ θ 0 + θ 1 x \ln h = \ln {\theta _0}{\rm{ + }}{\theta _{\rm{1}}}x lnh=lnθ0​+θ1​x，记 A = ln ⁡ θ 0 A=\ln {\theta _0} A=lnθ0​ ， h ˉ = ln ⁡ h \bar h=\ln h hˉ=lnh可得 h ˉ = θ 1 x + A \bar h = {\theta _{\rm{1}}}x{\rm{ + }}A hˉ=θ1​x+A，这是一个一次函数的形式。 当有多个样本点，需要提前把每个样本的 h ˉ \bar h hˉ解出来 h ˉ 0 = θ 1 x 0 + A h ˉ 1 = θ 1 x 1 + A ⋮ h ˉ m − 1 = θ 1 x m − 1 + A \begin{array}{l} {{\bar h_0} = {\theta _1}{x_0} +A}\\ {{\bar h_1} = {\theta _1}{x_1} +A}\\ \vdots \\ {{\bar h_{m - 1}} = {\theta _1}{x_{m - 1}} +A} \end{array} hˉ0​=θ1​x0​+Ahˉ1​=θ1​x1​+A⋮hˉm−1​=θ1​xm−1​+A​

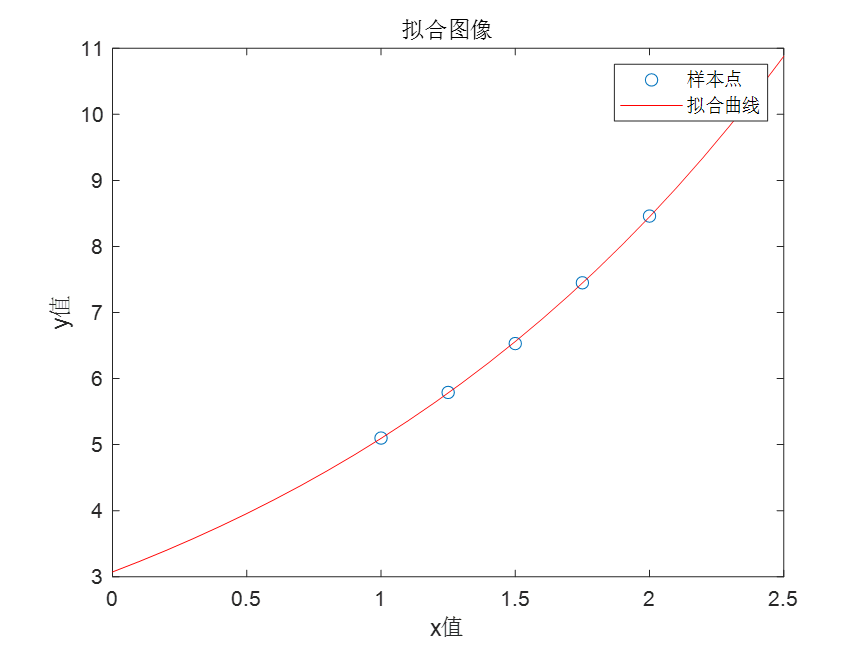
显然 X {\rm X} X矩阵和参数矩阵分别为： [ x 0 1 x 1 1 ⋮ ⋮ x m − 1 1 ] 以及 [ θ 1 A ] \begin{bmatrix} x_0 &1\\ x_1 &1\\ \vdots &\vdots \\ x_{m-1} &1\\ \end{bmatrix} 以及 \begin{bmatrix} {\theta_1} \\ A\\ \end{bmatrix} ​x0​x1​⋮xm−1​​11⋮1​ ​以及[θ1​A​] 用解一次函数的方式解出两个参数， θ 0 = e A {\theta_0}=e^A θ0​=eA解出 θ 0 {\theta_0} θ0​，这样两个参数就都求解出来了。

求得参数分别是 [ θ 1 θ 0 ] = [ 0.5057 3.0725 ] \begin{bmatrix} {\theta_1} \\ {\theta_0}\\ \end{bmatrix}= \begin{bmatrix} 0.5057 \\ 3.0725\\ \end{bmatrix} [θ1​θ0​​]=[0.50573.0725​] 注意参数 θ 0 {\theta_0} θ0​和 θ 1 {\theta_1} θ1​的输出顺序，代入待拟合的函数中得到 h = 3.0725 e 0.5057 x h=3.0725{\rm{e}^{0.5057{x}}} h=3.0725e0.5057x

参考文章： [1] 一文让你彻底搞懂最小二乘法（超详细推导） [2] 线性代数（十三）投影 [3] QR分解

码字不易难免打错, 发现错误欢迎指出， 万分感谢！！!