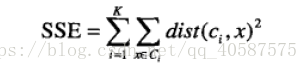| 数据挖掘 | 您所在的位置:网站首页 › 多维kmeans聚类 › 数据挖掘 |
数据挖掘
|
概念:
聚类分析(cluster analysis ):是一组将研究对象分为相对同质的群组(clusters)的统计分析技术。聚类分析也叫分类分析,或者数值分类。聚类的输入是一组未被标记的样本,聚类根据数据自身的距离或者相似度将其划分成若干个组,划分的原则是组内距离最小化而组间(外部)距离最大化。聚类和分类的不同在于:聚类所要求划分的类是未知的。
聚类度量的方法:分距离和相似度来度量。
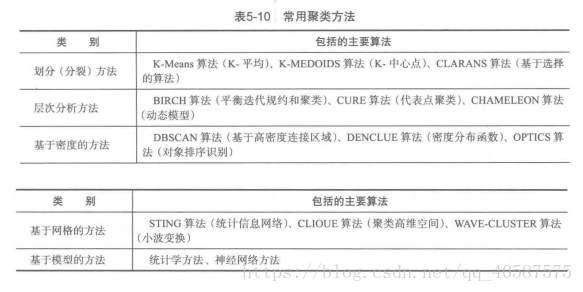
聚类研究分析的方法: 1.层次的方法(hierarchical method) 2.划分方法(partitioning method) 3.基于密度的方法(density-based method)DBSCAN 4.基于网格的方法(grid-based method) 5.基于模型的方法(model-based method) •受离群点的影响较大,由于其迭代每次的中心点到全部样本点的距离和的平均值。 优点: 原理简单 速度快 对大数据集有比较好的伸缩性缺点: 需要指定聚类 数量K 对异常值敏感 对初始值敏感•以欧式距离来衡量距离大小,使用误差平方和(Sum of the Squared Error,SSE)作为聚类的目标函数:
k表示k个聚类中心,ci表示第几个中心,dist表示的是欧几里得距离
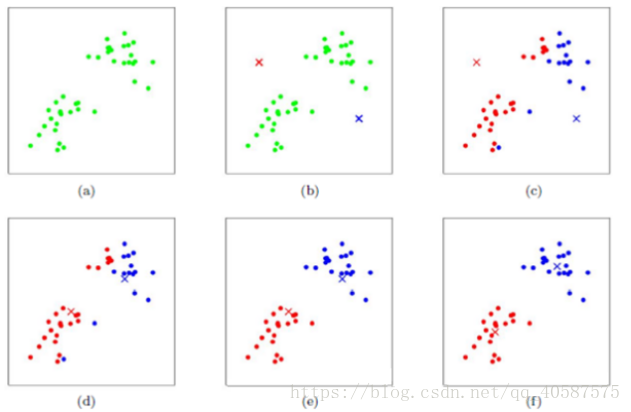
•算法步骤; •创建k个点作为初始的质心点(随机选择) •当任意一个点的簇分配结果发生改变时 • 对数据集中的每一个数据点 • 对每一个质心 • 计算质心与数据点的距离 • 将数据点分配到距离最近的簇 • 对每一个簇,计算簇中所有点的均值,并将均值作为质心 •算法图示:
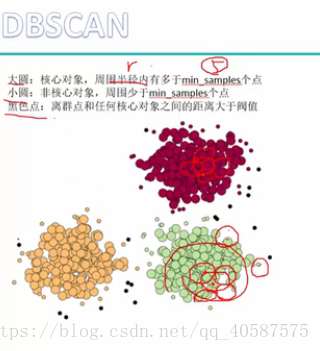
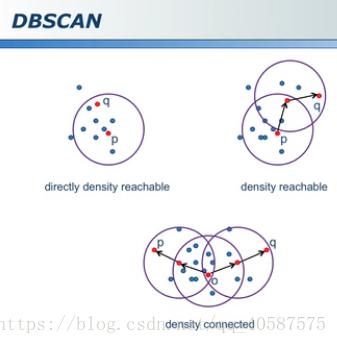
有关于 .A 的用法:(flatten()函数可以是多维数组变换成一维数组, .A 则使得matrix 形式转化成 array 形式) >>> import numpy as np >>> demo_a2 = np.mat([[1,3],[2,4],[3,5]]) >>> demo_a2 matrix([[1, 3], [2, 4], [3, 5]]) >>> demo_a2.flatten() matrix([[1, 3, 2, 4, 3, 5]]) >>> demo_a2.flatten().A array([[1, 3, 2, 4, 3, 5]]) >>> demo_a2.flatten().A[0] array([1, 3, 2, 4, 3, 5])#定义一个欧式距离的函数 : #coding=gbk ''' Created on 2018年7月17日 @author: Administrator ''' # k-means 算法python实现 import numpy as np def distEclud(vecA, vecB): #定义一个欧式距离的函数 return np.sqrt(np.sum(np.power(vecA - vecB, 2))) print('----test_distEclud-----') vecA, vecB = np.array([1,1]), np.array([2,1]) distance = distEclud(vecA, vecB) print(distance) # 1.0 计算两点之间的距离随机设置k个中心点: def randCent(dataSet, k): #第一个中心点初始化 n = np.shape(dataSet)[1] centroids = np.mat(np.zeros([k, n])) #创建 k 行 n列的全为0 的矩阵 for j in range(n): minj = np.min(dataSet[:,j]) #获得第j 列的最小值 rangej = float(np.max(dataSet[:,j]) - minj) #得到最大值与最小值之间的范围 #获得输出为 K 行 1 列的数据,并且使其在数据集范围内 centroids[:,j] = np.mat(minj + rangej * np.random.rand(k, 1)) return centroids print('----test_randCent-----') dataSet1 = np.array([[1,2],[3,6],[8,10],[12,23],[10,11],[13,18]]) print(dataSet1[1,:]) r = randCent(dataSet1, 2) print(r) # [[ 8.83544015 16.75467081] # [ 2.85688493 4.4799291 ]] np.random.seed(666) #定义一个随机种子 rand_num = np.random.rand(3,1) #输出为3行1 列,随机数在 0 到 1 之间 print(rand_num) # [[0.70043712] # [0.84418664] # [0.67651434]] test = np.mat(np.zeros([3,2])) #此处的 zeros 函数内的矩阵形式需要加中括号 [] print(test) # [[0. 0.] #打印出 3行 2列的矩阵 # [0. 0.] # [0. 0.]]定义KMeans函数: #参数: dataSet 样本点, K 簇的个数 #disMeans 距离, 默认使用欧式距离, createCent 初始中心点的选取 def KMeans(dataSet, k, distMeans= distEclud, createCent= randCent): m = np.shape(dataSet)[0] #得到行数,即为样本数 clusterAssement = np.mat(np.zeros([m,2])) #创建 m 行 2 列的矩阵 centroids = createCent(dataSet, k) #初始化 k 个中心点 clusterChanged = True while clusterChanged: clusterChanged = False for i in range(m): minDist = np.inf #初始设置值为无穷大 minIndex = -1 for j in range(k): # j循环,先计算 k个中心点到1 个样本的距离,在进行i循环,计算得到k个中心点到全部样本点的距离 distJ = distMeans(centroids[j,:], dataSet[i,:]) if distJ < minDist: minDist = distJ #更新 最小的距离 minIndex = j if clusterAssement[i,0] != minIndex: #如果中心点不变化的时候, 则终止循环 clusterChanged = True clusterAssement[i,:] = minIndex, minDist**2 #将 index,k值中心点 和 最小距离存入到数组中 print(centroids) #更换中心点的位置 for cent in range(k): ptsInClust = dataSet[np.nonzero(clusterAssement[:,0].A == cent)[0]] #分别找到属于k类的数据 centroids[cent,:] = np.mean(ptsInClust, axis = 0) #得到更新后的中心点 return centroids, clusterAssement print('------test-----') demo_a = np.array([[1,0],[0,2],[0,0]]) non_a = np.nonzero(demo_a) print(demo_a) # [[1 0] # [0 2] # [0 0]] print(non_a) # 输出的第一行为 行数, 第二行为列数,意思为 1行1列的数 和2行2列的数 是非0数 # (array([0, 1], dtype=int64), array([0, 1], dtype=int64)) demo_a1 = np.array([1,2,0,0,1]) #当只有一行时 non_a1 = np.nonzero(demo_a1) print(non_a1) # (array([0, 1, 4], dtype=int64),) a1 = np.inf > 100000 print(a1) # True inf 是无穷大 print('---------- test KMeans ---------') dataSet = np.mat([[ 0.90796996 ,5.05836784],[-2.88425582 , 0.01687006], [-3.3447423 , -1.01730512],[-0.32810867 , 0.48063528] ,[ 1.90508653 , 3.530091 ] ,[-3.00984169 , 2.66771831] ,[-3.38237045 ,-2.9473363 ] ,[ 2.22463036 ,-1.37361589] ,[ 2.54391447 , 3.21299611] ,[-2.46154315 , 2.78737555] ,[-3.38237045 ,-2.9473363 ] ,[ 2.8692781 ,-2.54779119] ,[ 2.6265299 , 3.10868015] ,[-2.46154315 , 2.78737555] ,[-3.38237045 ,-2.9473363 ] ,[ 2.80293085 ,-2.7315146 ]]) print(dataSet) center, cluster = KMeans(dataSet, 2) print('----') print(center) # [[-1.05990877 -2.0619207 ] # [-0.03469197 2.95415497]] print('----') print(cluster) # [[ 1. 5.31632331] # [ 0. 7.6496132 ] # [ 0. 6.31168598] # [ 1. 6.20439303] # [ 1. 4.09444295] # [ 1. 8.93356179] # [ 0. 6.17778903] # [ 0. 11.26196081] # [ 1. 6.71620993] # [ 1. 5.917422 ] # [ 0. 6.17778903] # [ 0. 15.67457959] # [ 1. 7.1059799 ] # [ 1. 5.917422 ] # [ 0. 6.17778903] # [ 0. 15.36988591]]python中kmeans的参数: sklearn.cluster.KMeans( n_clusters=8, init='k-means++', n_init=10, max_iter=300, tol=0.0001, precompute_distances='auto', verbose=0, random_state=None, copy_x=True, n_jobs=1, algorithm='auto' ) n_clusters: 簇的个数,即你想聚成几类 init: 初始簇中心的获取方法 n_init: 获取初始簇中心的更迭次数,为了弥补初始质心的影响,算法默认会初始10个质心,实现算法,然后返回最好的结果。 max_iter: 最大迭代次数(因为kmeans算法的实现需要迭代) tol: 容忍度,即kmeans运行准则收敛的条件 precompute_distances:是否需要提前计算距离,这个参数会在空间和时间之间做权衡,如果是True 会把整个距离矩阵都放到内存中,auto 会默认在数据样本大于featurs*samples 的数量大于12e6 的时候False,False 时核心实现的方法是利用Cpython 来实现的 verbose: 冗长模式(不太懂是啥意思,反正一般不去改默认值) random_state: 随机生成簇中心的状态条件。 copy_x: 对是否修改数据的一个标记,如果True,即复制了就不会修改数据。bool 在scikit-learn 很多接口中都会有这个参数的,就是是否对输入数据继续copy 操作,以便不修改用户的输入数据。这个要理解Python 的内存机制才会比较清楚。 n_jobs: 并行设置 algorithm: kmeans的实现算法,有:’auto’, ‘full’, ‘elkan’, 其中 ‘full’表示用EM方式实现 虽然有很多参数,但是都已经给出了默认值。所以我们一般不需要去传入这些参数,参数的。可以根据实际需要来调用。 •基于密度的方法; •DBSCAN (需要指定半径,对离群点的寻找作用很大): •大圆:核心对象,周围半径内有多于min_samples 个点 •小圆:非核心对象,周围少于 min_samples 个点 •黑色点:离群点和任何核心对象之间的距离大于阈值
参考:https://blog.csdn.net/taoyanqi8932/article/details/53727841 |
【本文地址】