| 【通信原理 入坑之路】 | 您所在的位置:网站首页 › 复数对应的点怎么看 › 【通信原理 入坑之路】 |
【通信原理 入坑之路】
|
写在前面:本博客是《深入浅出通信原理》的学习笔记,仅供个人学习参考使用 文章目录 一. IQ调制与解调的原理与过程1.1 利用旋转向量理解IQ调制(正交调制)1.2 利用旋转向量理解IQ解调 二.PSK(相移键控)和IQ调制的关系:2.1 用IQ调制实现QPSK调制2.2 用IQ调制实现8PSK调制 三. QAM调制与IQ调制的关系四.星座图一些性质的分析4.1 星座图受不同噪声干扰的情况分析 一. IQ调制与解调的原理与过程IQ调制的定义是:“IQ调制就是数据分为两路,分别进行载波调制,两路载波相互正交。I是in-phase(同相), q是 quadrature(正交)” 我们通过下面的示意图介绍IQ调制的过程: 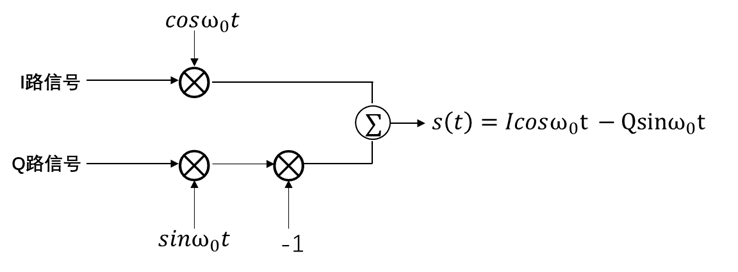
首先,信号分成两路:I路和Q路(为了方便理解我们把这两路信号先用字母I和Q代替) I路信号与 c o s ω 0 t cosω_0t cosω0t相乘,变成: I c o s ω 0 t Icosω_0t Icosω0t;Q路信号先与 s i n ω 0 t sinω_0t sinω0t相乘,再乘上-1,变成 − Q s i n ω 0 t -Qsinω_0t −Qsinω0t 接着,两路信号回合求和,变成IQ调制信号 s ( t ) = I c o s ω 0 t − Q s i n ω 0 t s(t) = Icosω_0t - Qsinω_0t s(t)=Icosω0t−Qsinω0t 有没有更加简单的表示方法?—— 有! 还记得我们在复变函数里面的知识吗? e j ω 0 t = c o s ω 0 t + j s i n ω 0 t e^{jω_0t} = cosω_0t + jsinω_0t ejω0t=cosω0t+jsinω0t 而我们可以把IQ信号用一个复数: I + j Q I + jQ I+jQ来表示,那么这个 I + j Q I + jQ I+jQ信号在复平面上就对应一个点 ( I + j Q ) e j ω 0 t = ( I + j Q ) ( c o s ω 0 t + j s i n ω 0 t ) = I c o s ω 0 t + j I s i n ω 0 t + j Q c o s ω 0 t − Q s i n ω 0 t (I + jQ)e^{jω_0t}\\ =(I+jQ)(cosω_0t + jsinω_0t)\\ =Icosω_0t + jIsinω_0t + jQcosω_0t - Qsinω_0t (I+jQ)ejω0t=(I+jQ)(cosω0t+jsinω0t)=Icosω0t+jIsinω0t+jQcosω0t−Qsinω0t 如果我们取运算结果的实部Re,就有: R e [ ( I + j Q ) e j ω 0 t ] = I c o s ω 0 t − Q s i n ω 0 t Re[(I + jQ)e^{jω_0t}] = Icosω_0t - Qsinω_0t Re[(I+jQ)ejω0t]=Icosω0t−Qsinω0t 那么,IQ调制的过程就可以简化为下图所示: 
对于IQ解调,也不困难,就是对 s ( t ) s(t) s(t)信号乘上 c o s ω 0 t cosω_0t cosω0t,再进行: 2 T ∫ − T 2 T 2 s ( t ) c o s ω 0 t \frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}s(t)cosω_0t T2∫−2T2Ts(t)cosω0t 这样的积分,就可以换原得到 I I I信号 对 s ( t ) s(t) s(t)信号乘以 − s i n ω 0 t -sinω_0t −sinω0t,再进行: 2 T ∫ − T 2 T 2 s ( t ) s i n ω 0 t \frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}s(t)sinω_0t T2∫−2T2Ts(t)sinω0t 这样的积分,即可换原得到 Q Q Q信号 1.1 利用旋转向量理解IQ调制(正交调制)我们回顾一下IQ调制的框图: 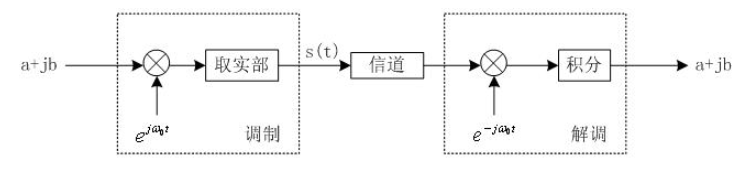
如果我们设I路信号a的值为 + 1 2 +\frac{1}{\sqrt{2}} +2 1,Q路信号b的值为 + 1 2 +\frac{1}{\sqrt{2}} +2 1,那么a+jb就可以用下面的旋转向量表示: 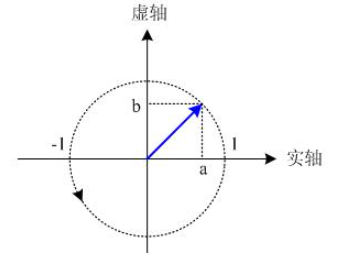
根据IQ调制的框图,我们需要将a + jb 与旋转向量 e j ω 0 t e^{jω_0t} ejω0t相乘,那么根据复数的乘法意义: 复数乘法中,积的模等于模的积;积的相位角等于两个乘数相位角的加和! 因此,a+jb和 e j ω 0 t e^{jω_0t} ejω0t相乘,得到的依然是在上图那个位置的向量,并且会绕逆时针旋转! 该旋转向量在实轴上的投影,就等于我们的调制信号 s ( t ) = a c o s ( ω 0 t ) − b s i n ( ω 0 t ) s(t) = acos(ω_0t) - bsin(ω_0t) s(t)=acos(ω0t)−bsin(ω0t)! 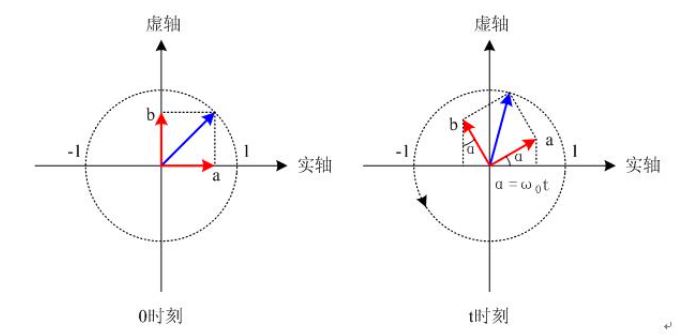
合成蓝色向量的两个红色向量分别代表I路信号和Q路信号。(而蓝色向量也可以看作是a+jb信号和 e j ω 0 t e^{jω_0t} ejω0t相乘的结果)在蓝色信号逆时针旋转的过程中,两个红色信号(I, Q信号)总时保持相互垂直),因此,IQ调制就被叫做正交调制了 1.2 利用旋转向量理解IQ解调和BPSK解调类似,假设我们接收到的
s
(
t
)
s(t)
s(t)信号是一个个的旋转向量,它们在不同接受时间(下图所示为t = 0和某t时刻)的位置如下: 不过,真实情况下,我们就受到的并不是旋转向量,(旋转向量只是我们便于理解设想出来的) 实际上接收到的是 s ( t ) = a c o s ( ω 0 t ) − b s i n ( ω 0 t ) s(t) = acos(ω_0t) - bsin(ω_0t) s(t)=acos(ω0t)−bsin(ω0t),应该怎么做呢? 下面揭晓: s ( t ) = a c o s ( ω 0 t ) − b s i n ( ω 0 t ) = a 2 ( e j ω 0 t + e − j ω 0 t ) + j b 2 ( e j ω 0 t − e − j ω 0 t ) = ( a 2 + j b 2 ) e j ω 0 t + ( a 2 − j b 2 ) e − j ω 0 t \begin{aligned} s(t) &= acos(ω_0t) - bsin(ω_0t)\\ &=\frac{a}{2}(e^{jω_0t} + e^{-jω_0t}) +\frac{jb}{2}(e^{jω_0t} - e^{-jω_0t})\\ &=(\frac{a}{2} + \frac{jb}{2})e^{jω_0t} + (\frac{a}{2} - \frac{jb}{2})e^{-jω_0t} \end{aligned} s(t)=acos(ω0t)−bsin(ω0t)=2a(ejω0t+e−jω0t)+2jb(ejω0t−e−jω0t)=(2a+2jb)ejω0t+(2a−2jb)e−jω0t 我们乘上一个 e − j ω 0 t e^{-jω_0t} e−jω0t,就变成了: ( a 2 + j b 2 ) + ( a 2 − j b 2 ) e − 2 j ω 0 t (\frac{a}{2} + \frac{jb}{2}) + (\frac{a}{2} - \frac{jb}{2})e^{-2jω_0t} (2a+2jb)+(2a−2jb)e−2jω0t 再乘以2后再经过积分或者低通滤波,就可以得到a+jb,即I, Q信号了 1 T ∫ − T 2 T 2 [ 2 ( a 2 + j b 2 ) + ( a 2 − j b 2 ) e − 2 j ω 0 t ] d t = a + j b \frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}[2(\frac{a}{2} + \frac{jb}{2}) + (\frac{a}{2} - \frac{jb}{2})e^{-2jω_0t}]dt = a+jb T1∫−2T2T[2(2a+2jb)+(2a−2jb)e−2jω0t]dt=a+jb 二.PSK(相移键控)和IQ调制的关系:PSK:相移键控方法是通过改变载波信号的相位值来表示数字信号 1,0的。当然,在实际信号的传输过程中,经常会把二进制信号按照M个比特作为一组传输,这就是MPSK。(PSK调制幅度不变,改变相位) 比如说:如果我们把2个比特作为一组,那么每一组二进制信号就会有00,01,10,11四种组合方式,那么我们就需要 s ( t ) s(t) s(t)用4种不同的相位值分别来表示00,01,10和11,这样的调制方式我们成为QPSK调制。 2.1 用IQ调制实现QPSK调制首先,我们假设输入的 I I I路和 Q Q Q路信号分别为:+1+1、+1-1、-1+1、-1-1。那么根据上面IQ调制的流程图,我们分别看看输出的 s ( t ) s(t) s(t)信号是怎么样的: I I I路信号 Q Q Q路信号 s ( t ) s(t) s(t)+1+1 c o s ω 0 t − s i n ω 0 t = 2 c o s ( ω 0 t + Π 4 ) cosω_0t - sinω_0t = \sqrt{2}cos(ω_0t + \frac{Π}{4}) cosω0t−sinω0t=2 cos(ω0t+4Π)+1-1 c o s ω 0 t + s i n ω 0 t = 2 c o s ( ω 0 t + 3 Π 4 ) cosω_0t + sinω_0t = \sqrt{2}cos(ω_0t + \frac{3Π}{4}) cosω0t+sinω0t=2 cos(ω0t+43Π)-1+1 − c o s ω 0 t − s i n ω 0 t = 2 c o s ( ω 0 t + 5 Π 4 ) -cosω_0t - sinω_0t = \sqrt{2}cos(ω_0t + \frac{5Π}{4}) −cosω0t−sinω0t=2 cos(ω0t+45Π)-1-1 − c o s ω 0 t + s i n ω 0 t = 2 c o s ( ω 0 t + 7 Π 4 ) -cosω_0t + sinω_0t = \sqrt{2}cos(ω_0t + \frac{7Π}{4}) −cosω0t+sinω0t=2 cos(ω0t+47Π)如果我们要把 s ( t ) s(t) s(t)的幅度变成1,那么只需要将上面 I , Q I, Q I,Q信号对应第改为 + 1 2 +\frac{1}{\sqrt{2}} +2 1和 − 1 2 -\frac{1}{\sqrt{2}} −2 1即可 而我们发现: + 1 2 +\frac{1}{\sqrt{2}} +2 1 = s i n Π 4 sin\frac{Π}{4} sin4Π = c o s Π 4 cos\frac{Π}{4} cos4Π 下面,我们就可以建立二进制序列、I,Q信号和相位的对应关系了: 二进制序列IQ信号 s ( t ) s(t) s(t)相位00 + 1 2 +\frac{1}{\sqrt{2}} +2 1, + 1 2 +\frac{1}{\sqrt{2}} +2 1 Π 4 \frac{Π}{4} 4Π01 − 1 2 -\frac{1}{\sqrt{2}} −2 1, + 1 2 +\frac{1}{\sqrt{2}} +2 1 3 Π 4 \frac{3Π}{4} 43Π11 − 1 2 -\frac{1}{\sqrt{2}} −2 1, − 1 2 -\frac{1}{\sqrt{2}} −2 1 5 Π 4 \frac{5Π}{4} 45Π10 + 1 2 +\frac{1}{\sqrt{2}} +2 1, − 1 2 -\frac{1}{\sqrt{2}} −2 1 7 Π 4 \frac{7Π}{4} 47Π因此,MPSK调制的过程中,我们需要将输入信号(二进制序列)经过一定的映射(上表所示的映射关系)映射成对应的IQ信号,再经过运算得到 s ( t ) s(t) s(t)信号 因此,QPSK信号的正弦载波有4个可能的离散相位状态,每个载波相位携带2个二进制符号,其信号表示式为: s ( t ) = A c o s ( ω 0 t + θ ) s(t) = Acos(ω_0t + θ) s(t)=Acos(ω0t+θ) 下图是QPSK调制的星座图: 
而对于通过接受信号的星座图判断信号,则是看接收数据点距00,01,11,10这四个点的距离来判断接受信号到底是哪个。 2.2 用IQ调制实现8PSK调制在上面分析QPSK调制星座图的特征时,我们发现:发射信号点都是在单位圆的 1 4 \frac{1}{4} 41位置,那么同理,对于8PSK,发射信号点都是在单位圆的 1 8 \frac{1}{8} 81位置处。 输入信号被划分为3个比特一组,如果我们按照下面的对应关系,就可以得到星座图了: 输入信号IQ信号 s ( t ) s(t) s(t)相位000 c o s Π 8 , s i n Π 8 cos\frac{Π}{8}, sin\frac{Π}{8} cos8Π,sin8Π Π 8 \frac{Π}{8} 8Π001 s i n Π 8 , c o s Π 8 sin\frac{Π}{8},cos\frac{Π}{8} sin8Π,cos8Π 3 Π 8 \frac{3Π}{8} 83Π011 − s i n Π 8 , c o s Π 8 -sin\frac{Π}{8},cos\frac{Π}{8} −sin8Π,cos8Π 5 Π 8 \frac{5Π}{8} 85Π010 − c o s Π 8 , s i n Π 8 -cos\frac{Π}{8}, sin\frac{Π}{8} −cos8Π,sin8Π 7 Π 8 \frac{7Π}{8} 87Π110 − c o s Π 8 , − s i n Π 8 -cos\frac{Π}{8}, -sin\frac{Π}{8} −cos8Π,−sin8Π 9 Π 8 \frac{9Π}{8} 89Π111 − s i n Π 8 , − c o s Π 8 -sin\frac{Π}{8},-cos\frac{Π}{8} −sin8Π,−cos8Π 11 Π 8 \frac{11Π}{8} 811Π101 s i n Π 8 , − c o s Π 8 sin\frac{Π}{8},-cos\frac{Π}{8} sin8Π,−cos8Π 13 Π 8 \frac{13Π}{8} 813Π100 c o s Π 8 , − s i n Π 8 cos\frac{Π}{8}, -sin\frac{Π}{8} cos8Π,−sin8Π 15 Π 8 \frac{15Π}{8} 815Π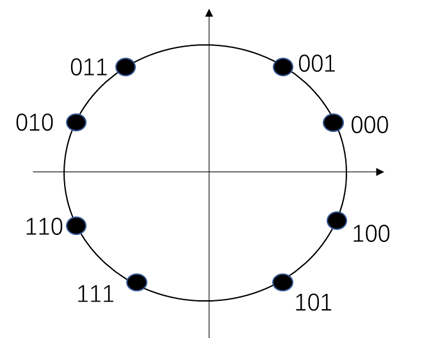
因此星座图的作用主要是在调制时用于映射(比如QPSK,16QAM,64QAM等),而接收时用于判断发送的到底是哪个点,从而正确解调数据。 三. QAM调制与IQ调制的关系本节的学习中,我们想通过QAM的矩形星座图分析星座图的结构: 
我们看看用IQ调制实现16QAM调制时,输入比特(被划分为4个4个一组)和IQ信号的映射关系: 输入比特I、Q信号0000+3A、+3A0001+A、+3A0011-A、+3A0010-3A、+3A0110-3A、+A0111-A、+A0101+A、+A0100+3A、+A1100+3A、-A1101+A、-A1111-A、-A1110-3A、-A1010-3A、-3A1011-A、-3A1001+A、-3A1000+3A、-3A那么,我们通过这个表可以知道,矩形16-QAM星座图有3个幅值,分别是: 3 2 A 3\sqrt{2}A 32 A、 10 A \sqrt{10}A 10 A、 2 A \sqrt{2}A 2 A 当然,我们通过矩形星座图也能够一目了然: 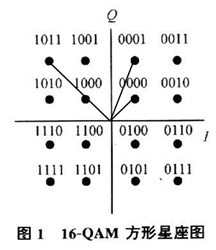
注意:对于16QAM调制,我们不是将4个bit划分为一组吗,那么它们在输入后“兵分两路”时,是把这4个bit分两路,一路2个bit,分别给I和Q,这样,I路就会有 2 2 = 4 2^2 = 4 22=4个不同幅度的电平、Q路也会有4个不同幅度的电平,又由于I,Q信号正交(互不相关),因此任意一个I的幅度和任意一个Q幅度的组合都会对应一个星座点。一共就会有4x4 = 16种组合状态 四.星座图一些性质的分析星座图有几个重要的参数: 最小欧几里德距离:它是M-QAM信号星座图上星座点之间的最小距离。该参数反映了M-QAM信号抗高斯白噪声的能力(最小欧几里德距离越大,信号抗高斯白噪声的能力越强),可以通过优化星座图的分布来获得最大值。最小相位偏移:最小相位偏移是M-QAM信号星座点相位的最小偏移,该参数反映了MQAM信号抗相对抖动能力和对时钟恢复精确度的敏感性,同样地,可以通过优化星座点的分布来获得最大值,以获得更优的传输性能。我们来看看16QAM的两种星座图: 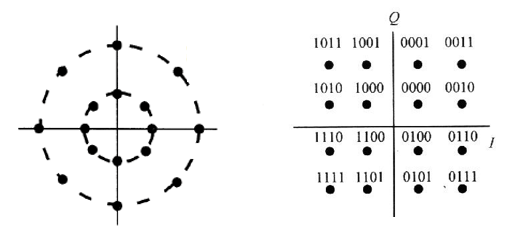
通过刚刚的分析我们可以知道: 矩形星座图有3个幅值,圆形星座图有2个幅值。矩形星座图有12个相位值,而圆形星座图有8个相位值。圆形的最小相位偏移为45°,而矩形星座图的最小相位偏移为18°(由此可见,圆形星座图的最小相位偏移比矩形星座图大,其抗相位抖动的能力较强) 4.1 星座图受不同噪声干扰的情况分析【1】白噪声干扰:噪声随机,落点会围绕理想值成云状分布(awgn加性高斯白噪声) 
【2】相位噪声:相位噪声是一段期间内振荡器的相对相位不稳定的情况,在星座图上显示出围绕图形中心旋转的情况,如下图所示: 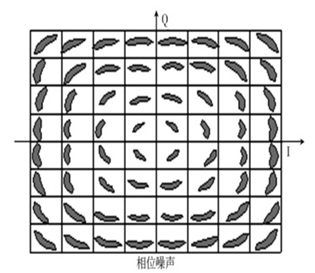
【3】增益压缩: 由于信号压缩失真,出现非方正星座图。QAM峰值越大,失真越大 
【4】载波抑制: 表现为星座图整体平移 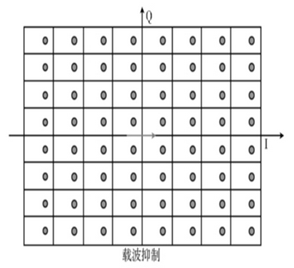
【5】I、Q 幅度不平衡 
【6】I、Q 正交不平衡 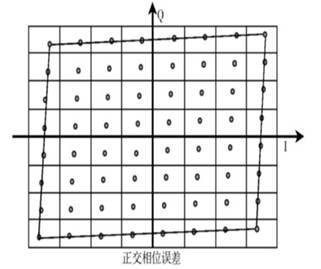
|
【本文地址】
 相同地,我们会用一个和接收到的向量旋转方向相反的,幅值相同,频率相同的旋转向量与它相乘: 对应上图的,我们所用的本地旋转向量如图所示:
相同地,我们会用一个和接收到的向量旋转方向相反的,幅值相同,频率相同的旋转向量与它相乘: 对应上图的,我们所用的本地旋转向量如图所示:  那么,它们相乘,就可以得到静止的向量,整个静止的向量对应的实部就是I路信号,对应的虚部就是Q路信号。
那么,它们相乘,就可以得到静止的向量,整个静止的向量对应的实部就是I路信号,对应的虚部就是Q路信号。