| 复三角函数 | 您所在的位置：网站首页 › 复指数函数如何化成三角函数 › 复三角函数 |
复三角函数
|
在复变函数中，我们借助复指数函数将三角函数的定义域延拓到复数域上去，得到复三角函数。 目录 1 定义 2 性质 3 几何意义 4 上下节 定义[]我们定义如下形式的两个复变函数为正弦函数以及余弦函数： sin z = e i z − e − i z 2 i , cos z = e i z + e − i z 2 {\displaystyle \sin z={\dfrac {{\text{e}}^{{\text{i}}z}-{\text{e}}^{-{\text{i}}z}}{2{\text{i}}}},\quad \cos z={\dfrac {{\text{e}}^{{\text{i}}z}+{\text{e}}^{-{\text{i}}z}}{2}}} 这两个函数称为基本三角函数（也有加上后面定义的正切函数一起称呼的说法），我们用这两个函数表示其余四个三角函数，如下，分别称作正切函数、余切函数、正割函数以及余割函数： tan z = sin z cos z = e i z − e − i z i ( e i z + e − i z ) cot z = cos z sin z = i ( e i z + e − i z ) e i z − e − i z sec z = 1 cos z = 2 e i z + e − i z csc z = 1 sin z = 2 i e i z − e − i z . {\displaystyle {\begin{aligned}\tan z&={\dfrac {\sin z}{\cos z}}={\dfrac {{\text{e}}^{{\text{i}}z}-{\text{e}}^{-{\text{i}}z}}{{\text{i}}({\text{e}}^{{\text{i}}z}+{\text{e}}^{-{\text{i}}z})}}\\\cot z&={\dfrac {\cos z}{\sin z}}={\dfrac {{\text{i}}({\text{e}}^{{\text{i}}z}+{\text{e}}^{-{\text{i}}z})}{{\text{e}}^{{\text{i}}z}-{\text{e}}^{-{\text{i}}z}}}\\\sec z&={\dfrac {1}{\cos z}}={\dfrac {2}{{\text{e}}^{{\text{i}}z}+{\text{e}}^{-{\text{i}}z}}}\\\csc z&={\dfrac {1}{\sin z}}={\dfrac {2{\text{i}}}{{\text{e}}^{{\text{i}}z}-{\text{e}}^{-{\text{i}}z}}}.\end{aligned}}} 以上六个复变函数统称为复三角函数，当 z {\displaystyle z} 取实数时就是普通的实三角函数。 性质[]由于上述六个复三角函数都是复指数函数通过有限次四则运算得到的，因此在定义域上都是解析的，它们的定义域是除去使得分母为零的点的 z {\displaystyle z} 平面。 特别地，如果 z = x + i y , x , y ∈ R {\displaystyle z=x+{\text{i}}y,x,y\in \mathbb {R} } ，那么下面的式子成立 sin z = sin x cosh y + i cos x sinh y ; {\displaystyle \sin z=\sin x\cosh y+{\text{i}}\cos x\sinh y;} cos z = cos x cosh y − i sin x sinh y . {\displaystyle \cos z=\cos x\cosh y-{\text{i}}\sin x\sinh y.}由于它是通过实三角函数延拓来的，因此也有很多性质和实三角函数类似，例如它们的奇偶性、周期性、零点、导数以及三角恒等式都可以不加修改的推广过来。唯一不同的是，它们都是无界函数，包括正弦函数以及余弦函数。 此外，还有下面的性质 ∀ z 1 , z 2 ∈ C , sin z 1 = sin z 2 ⟺ z 1 − z 2 = 2 k π ∨ z 1 + z 2 = ( 2 k + 1 ) π , k ∈ Z ; {\displaystyle \forall z_{1},z_{2}\in \mathbb {C} ,\sin z_{1}=\sin z_{2}\iff z_{1}-z_{2}=2k\pi \vee z_{1}+z_{2}=(2k+1)\pi ,k\in \mathbb {Z} ;} ∀ z 1 , z 2 ∈ C , cos z 1 = cos z 2 ⟺ z 1 − z 2 = 2 k π ∨ z 1 + z 2 = 2 k π , k ∈ Z ; {\displaystyle \forall z_{1},z_{2}\in \mathbb {C} ,\cos z_{1}=\cos z_{2}\iff z_{1}-z_{2}=2k\pi \vee z_{1}+z_{2}=2k\pi ,k\in \mathbb {Z} ;} ∀ z 1 , z 2 ∈ C , tan z 1 = tan z 2 ⟺ z 1 − z 2 = k π , k ∈ Z . {\displaystyle \forall z_{1},z_{2}\in \mathbb {C} ,\tan z_{1}=\tan z_{2}\iff z_{1}-z_{2}=k\pi ,k\in \mathbb {Z} .} 几何意义[]如果说复指数函数是将实部和虚部直线变为了极坐标上的射线和圆，那么复正弦函数就是将实部和虚部直线变为了椭圆和双曲线（的一支），我们还是按照复指数的讨论思路来讨论复正弦函数：①虚部不变改变实部；②实部不变改变虚部。以下我们假设 z = a + i b {\displaystyle z=a+{\text{i}}b} ，复三角函数 z 2 = sin z 1 {\displaystyle z_{2}=\sin z_{1}} ，我们依旧用虚线表示自变量曲线，实线表示因变量曲线。 ①先考虑特殊情况： a {\displaystyle a} 从 − π {\displaystyle -\pi } 变化到 π {\displaystyle \pi } ， b = 0 {\displaystyle b=0} ，其图象是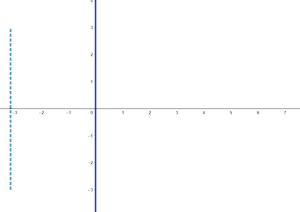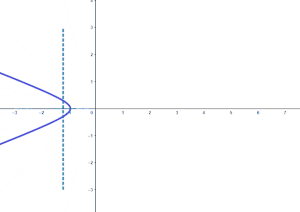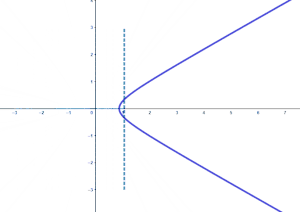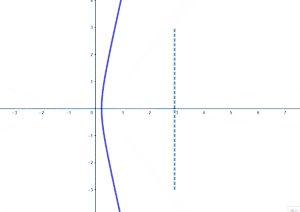 
可以发现其图像按照周期 2 π {\displaystyle 2\pi } 循环变化，实际上，经过推理可得出因变量曲线的方程是 ( x sin a ) 2 − ( y cos a ) 2 = 1 {\displaystyle \left({\dfrac {x}{\sin a}}\right)^{2}-\left({\dfrac {y}{\cos a}}\right)^{2}=1} ，它是双曲线（的一支）。实部决定了双曲线的轴长。 这种情况下因变量曲线是双曲线，它的运动周期是自变量 z {\displaystyle z} 的实部，这是复正弦函数的一个主要特点。 ②如果只改变实部，那么我们假设 a = 1 {\displaystyle a=1} ， b {\displaystyle b} 在某个原点的邻域内变化，有下面的图象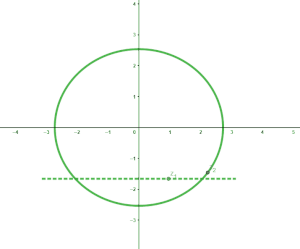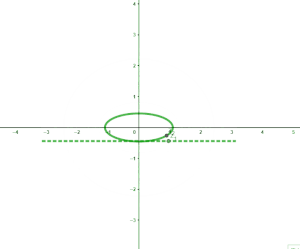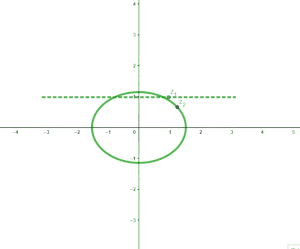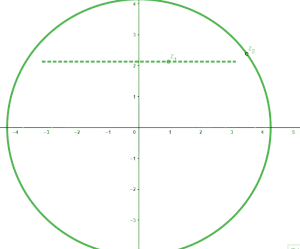 
自然，这是一个椭圆，可以证明它的方程是 ( x cosh b ) 2 + ( y sinh b ) 2 = 1 {\displaystyle \left({\dfrac {x}{\cosh b}}\right)^{2}+\left({\dfrac {y}{\sinh b}}\right)^{2}=1} ，它的轴长仅由自变量的虚部决定。 而整体的图像就是椭圆以及双曲线的矢量叠加，这两个是正交的。由于椭圆的交点与双曲线的焦点都是 ( ± 1 , 0 ) {\displaystyle (\pm 1,0)} ，因此实际上这个图象组成的是一个椭圆坐标系，这也是复正弦函数在椭圆坐标系上最直观的表现。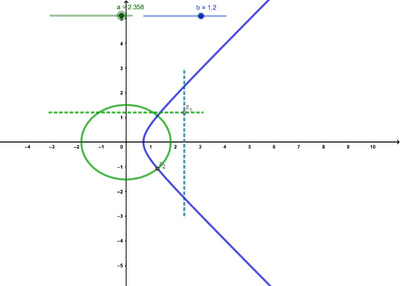 
上下节[]
上一节：复指数函数
下一节：复双曲函数
单复变函数论（学科代码：1104120，GB/T 13745—2009）
复数理论
复平面 ▪ 复数列 ▪ 棣莫弗公式 ▪ 复球面 ▪ 欧拉公式 ▪ 复几何
复变函数以及微分理论
复变函数的极限 ▪ 复变函数的连续性 ▪ 复变函数的导数 ▪ 解析函数 ▪ 复指数函数 ▪ 复三角函数 ▪ 复双曲函数 ▪ 复指数系函数的几何形态 ▪ 多值函数 ▪ 辐角函数 ▪ 复对数函数 ▪ 复根式函数 ▪ 复幂以及一般幂函数 ▪ 复反三角函数
复变函数的积分理论
复变函数的积分 ▪ Cauchy 积分定理 ▪ 复变函数的不定积分 ▪ Cauchy 积分公式 ▪ Liouville 定理 ▪ Cauchy 型积分
复变函数的级数理论
复数项级数 ▪ 复函数项级数、复幂级数 ▪ 解析函数的泰勒展式 ▪ 解析函数的零点性质 ▪ 解析函数的洛朗展式 ▪ 解析函数的孤立奇点 ▪ 解析函数的无穷远点性质 ▪ 留数理论 ▪ 留数的应用 ▪ 对数留数
复变函数的几何理论
解析变换 ▪ 分式线性变换 ▪ 共形映射 ▪ 解析开拓 ▪ 完全解析函数 ▪ 整函数 ▪ 亚纯函数
所在位置：数学（110）→ 函数论（11041）→ 单复变函数论（1104120）
|
这两个函数称为基本三角函数（也有加上后面定义的正切函数一起称呼的说法），我们用这两个函数表示其余四个三角函数，如下，分别称作正切函数、余切函数、正割函数以及余割函数：
tan
z
=
sin
z
cos
z
=
e
i
z
−
e
−
i
z
i
(
e
i
z
+
e
−
i
z
)
cot
z
=
cos
z
sin
z
=
i
(
e
i
z
+
e
−
i
z
)
e
i
z
−
e
−
i
z
sec
z
=
1
cos
z
=
2
e
i
z
+
e
−
i
z
csc
z
=
1
sin
z
=
2
i
e
i
z
−
e
−
i
z
.
{\displaystyle {\begin{aligned}\tan z&={\dfrac {\sin z}{\cos z}}={\dfrac {{\text{e}}^{{\text{i}}z}-{\text{e}}^{-{\text{i}}z}}{{\text{i}}({\text{e}}^{{\text{i}}z}+{\text{e}}^{-{\text{i}}z})}}\\\cot z&={\dfrac {\cos z}{\sin z}}={\dfrac {{\text{i}}({\text{e}}^{{\text{i}}z}+{\text{e}}^{-{\text{i}}z})}{{\text{e}}^{{\text{i}}z}-{\text{e}}^{-{\text{i}}z}}}\\\sec z&={\dfrac {1}{\cos z}}={\dfrac {2}{{\text{e}}^{{\text{i}}z}+{\text{e}}^{-{\text{i}}z}}}\\\csc z&={\dfrac {1}{\sin z}}={\dfrac {2{\text{i}}}{{\text{e}}^{{\text{i}}z}-{\text{e}}^{-{\text{i}}z}}}.\end{aligned}}}
以上六个复变函数统称为复三角函数，当
z
{\displaystyle z}
取实数时就是普通的实三角函数。
性质[]
，那么下面的式子成立
cos
z
=
cos
x
cosh
y
−
i
sin
x
sinh
y
.
{\displaystyle \cos z=\cos x\cosh y-{\text{i}}\sin x\sinh y.}
∀
z
1
,
z
2
∈
C
,
cos
z
1
=
cos
z
2
⟺
z
1
−
z
2
=
2
k
π
∨
z
1
+
z
2
=
2
k
π
,
k
∈
Z
;
{\displaystyle \forall z_{1},z_{2}\in \mathbb {C} ,\cos z_{1}=\cos z_{2}\iff z_{1}-z_{2}=2k\pi \vee z_{1}+z_{2}=2k\pi ,k\in \mathbb {Z} ;}
∀
z
1
,
z
2
∈
C
,
tan
z
1
=
tan
z
2
⟺
z
1
−
z
2
=
k
π
,
k
∈
Z
.
{\displaystyle \forall z_{1},z_{2}\in \mathbb {C} ,\tan z_{1}=\tan z_{2}\iff z_{1}-z_{2}=k\pi ,k\in \mathbb {Z} .}
几何意义[]
，复三角函数
z
2
=
sin
z
1
{\displaystyle z_{2}=\sin z_{1}}
，我们依旧用虚线表示自变量曲线，实线表示因变量曲线。
从
−
π
{\displaystyle -\pi }
变化到
π
{\displaystyle \pi }
，
b
=
0
{\displaystyle b=0}
，其图象是
循环变化，实际上，经过推理可得出因变量曲线的方程是
(
x
sin
a
)
2
−
(
y
cos
a
)
2
=
1
{\displaystyle \left({\dfrac {x}{\sin a}}\right)^{2}-\left({\dfrac {y}{\cos a}}\right)^{2}=1}
，它是双曲线（的一支）。实部决定了双曲线的轴长。
，
b
{\displaystyle b}
在某个原点的邻域内变化，有下面的图象
，它的轴长仅由自变量的虚部决定。
，因此实际上这个图象组成的是一个椭圆坐标系，这也是复正弦函数在椭圆坐标系上最直观的表现。
【本文地址】