| 有限元误差分析 | 您所在的位置:网站首页 › 固有频率分析 › 有限元误差分析 |
有限元误差分析
|
1. 前言
本文主要讨论有限元分析中的剪切自锁,体积自锁,沙漏模式和零能模式,这些问题通常会造成较大的计算误差,在有限元分析过程中要重点关注。 本文从有限元基础理论开始,首先介绍形函数与高斯积分,在求解高斯积分过程中,根据积分点的选择可以分为完全积分和缩减积分,而上述这些问题就出现于完全积分和缩减积分的过程中。在这之后重点描述剪切和体积自锁,沙漏模式和零能模式的概念,原理以及相应的工程案例,最后讨论如何避免和解决该类问题。 2. 有限元基础理论 2.1 形函数在有限元分析中,通过节点位移和(位移)形函数便可以确定单元内任意一点的位移分布。仅以位移形函数为例,从字面上看就是定义了位移场形状的函数,即一种以节点位移为基础的插值关系。形函数是有限元的基石,在形式上是一个多项式。需要注意,相同种类的单元具有相同的形函数,因此在单元相连的节点处,位移形函数是连续的。但是当模型中存在多种类型的单元时,如处理梁单元和实体单元连接的问题,这时需要使用MPC添加某些节点间的位移关系,来保证(实体单元和梁单元)位移形函数在节点处连续。 如果想快速了解形函数可以阅读下面几篇文章,如果想深入了解形函数的构造可以查阅有限元理论的相关书籍。 《有限元简单科普之——形函数》 《05 -- 常见单元的形函数和坐标变换》 《7. 形函数、标准形以及等参元》 2.2 高斯积分高斯积分是一种求解数值积分的方法,非常适合对多项式或近似多项式形式的函数进行数值积分。 关于高斯积分的原理可以参考《有限元高斯积分点是什么?》 那么高斯积分是如何在有限元分析中应用的呢? 有限元分析的一般过程如下: 首先建立位移函数,之后通过几何方程建立位移与应变的关系,再通过平衡方程使用虚功原理求解单元的刚度矩阵: 其中,[B]矩阵为几何方程的矩阵,由形函数的偏导数构成,[D]矩阵表达了应力和应变的关系,仅与材料属性有关。通过高斯积分求解上式,得到单元的刚度矩阵。之后组装刚度矩阵,加上边界条件后就可以求得节点位移值。 因此,在有限元分析中,节点上的位移量是我们得到的最直接也是最精确的计算结果,应力和应变值是由位移值进一步计算得到的。所以在ANSYS APDL的后处理中,可以输出应力和应变的节点解与单元解,但是位移只能输出节点解(位移在节点处是连续的,无需区分节点解和单元解)。那么为什么应力和应变会有多种形式的解呢? 有限元软件得到节点的位移解之后,通过弹性力学方程先计算高斯积分点处的应力和应变,再通过相应的形函数插值到节点处。有的文章中将高斯点处的应力/应变解称为“单元解”,这个概念在ABAQUS中是正确的,但是在ANSYS APDL中,将插值得到的节点处的解称为“单元解”(或“单元角节点解”),而高斯点的解在后处理中并不能直接输出。 在ANSYS经典中如何查看高斯点的解可以参考《ansys查看积分点(高斯点)上应力的方法》 有了“单元解”后“节点解”是如何得到的呢? 上文提到位移场在节点处是连续的,而应力场和应变场是通过位移场求导得到,因此在节点处并不能保证连续。这时就会出现一个情况,当多个单元共用一个节点时,从不同单元推导得到的应力值无法保持一致。为了保证数值连续,通常会做平均处理,处理后得到的解就是“节点解”。 例如:单元A和单元B存在公共节点1, case1:查看单元解时,单元A上节点1的应力为11MPa,单元B上节点1的应力为9MPa; case2:查看节点解时,公共节点1的应力为10MPa; 关于后处理部分的详细介绍可参考: 《ANSYS 有限元分析 后处理 结点解与单元解》 3. 剪切自锁,体积自锁,沙漏模式和零能模式在描述剪切&体积自锁之前,还需要明确一些概念,包括单元的阶次,完全积分和缩减积分。 关于单元的阶次,根据划分后单元是否存在中节点可分为低阶单元和高阶单元,相信绝大部分的有限元学习者对这部分概念都很熟悉,所以不再赘述,重点说一下完全积分和缩减积分。 完全积分是指在高斯积分的过程中所采用的积分点数目足以对单元刚度矩阵的多项式进行精确求解,规则为N个高斯点可以对2N-1阶多项式函数精确求解。以四边形单元为例,低阶单元和高阶单元的积分点布置如下图所示,低阶单元每个方向2个积分点,高阶单元每个方向3个积分点。 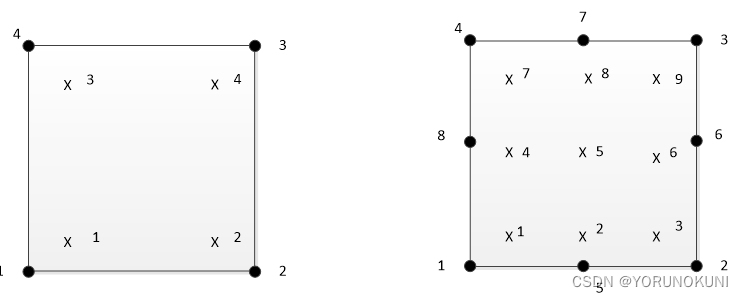 图3.1 完全积分时四边形单元的积分点布置
图3.1 完全积分时四边形单元的积分点布置
缩减积分即采用的积分点不足以对多项式函数进行精确求解,以四边形单元为例,低阶单元和高阶单元的积分点布置如下图所示。 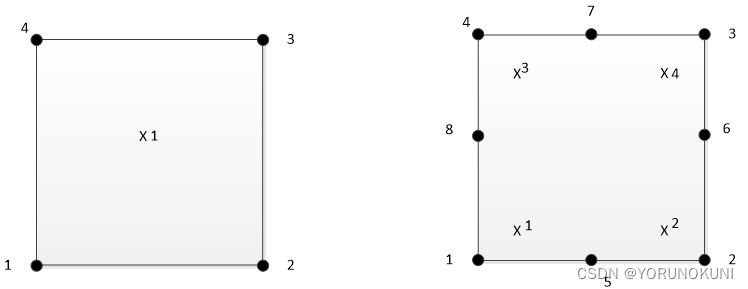 图3.2 缩减积分时四边形单元的积分点布置
图3.2 缩减积分时四边形单元的积分点布置
那么在完全积分和缩减积分的过程中,剪切自锁等一系列现象是如何发生的呢? 3.1 剪切自锁 3.1.1 原理剪切自锁是在以弯曲变形为主的问题中,完全积分低阶单元呈现出的“刚度过硬”现象。经常使用纯弯曲梁的例子来讨论剪切自锁问题,以低阶四边形单元为例,纯弯曲状态下的理想的变形如图3.3a所示,弯曲后侧面两条边的夹角仍是90°,不存在剪切变形。如果使用完全积分的低阶单元,由于低阶单元的边不能弯曲,侧面两条边的夹角发生了变化不再是90°,因此产生了剪切变形,如图3.3b所示。由于剪切变形的存在消耗了部分应变能,导致弯曲变形减少,结构弯曲刚度增大。当发生剪切自锁时,计算得到的弯曲变形会小于理论值。 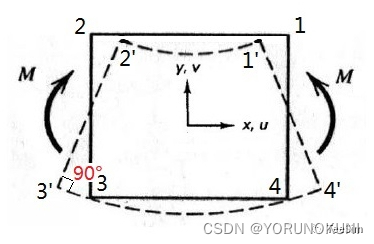 图3.3a 纯弯曲下的理想变形
图3.3a 纯弯曲下的理想变形
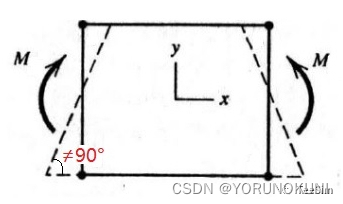 图3.3b 纯弯曲下低阶单元的变形
3.1.2 实例
图3.3b 纯弯曲下低阶单元的变形
3.1.2 实例
模型:纯弯曲梁,一端固定,一端受到1e6N·mm的力矩,梁的长度为1500mm,截面为100mm×100mm,材料为默认结构钢。 根据梁的挠度计算公式: 下面将建立多个算例研究剪切自锁的产生条件与解决方法。 实例1:使用beam188单元 默认网格,求解后查看Y轴定向变形和切应力 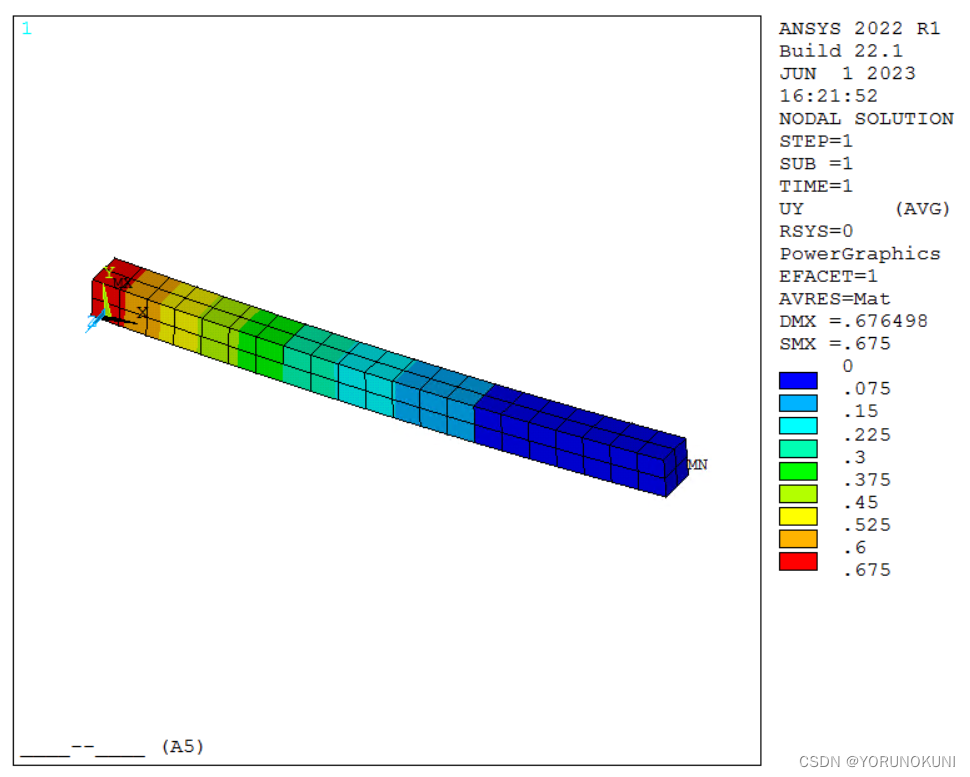 图3.4a beam188下变形结果
图3.4a beam188下变形结果
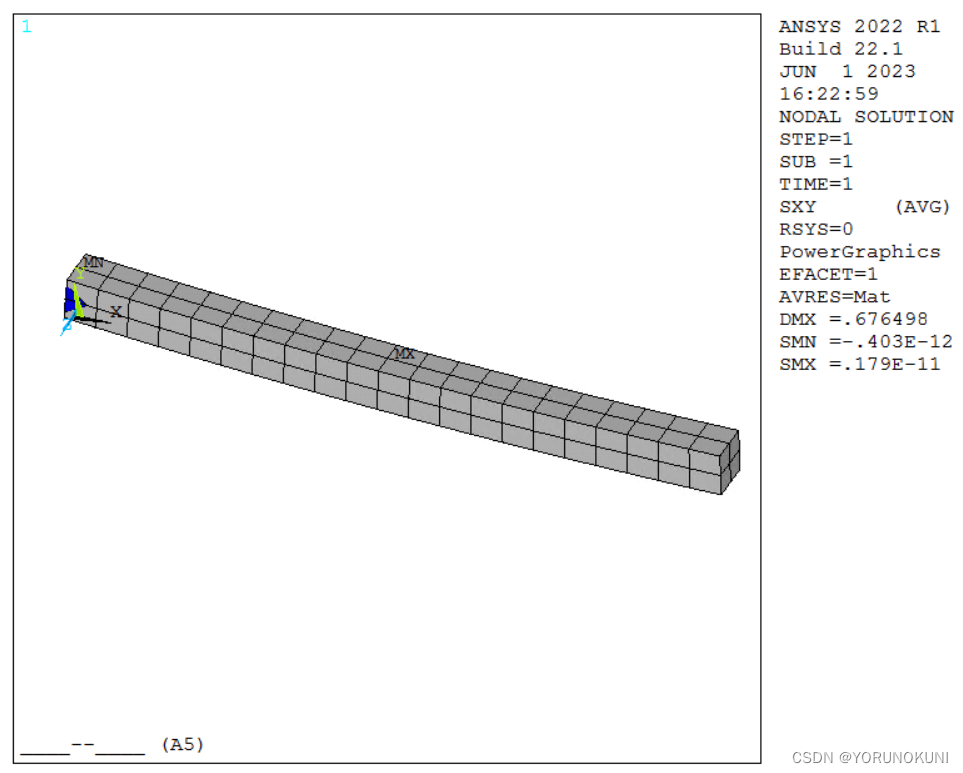 图3.4b beam188下切应力结果
图3.4b beam188下切应力结果
实例2:使用默认设置(缩减积分,solid186单元) 使用默认网格(全局75mm),查看Y轴定向变形和切应力,如下图所示。可以看出,梁的最大变形为0.672mm,虽然网格密度不大,但计算结果与理论解的相对误差仅为-0.44%。在查看切应力时发现固定约束处出现了应力奇异,因此选择梁的中间段输出切应力值。当采用实体186单元并缩减积分时,梁中间段出现了切应力但数值很小,且随着网格密度的增加逐渐趋近于0。 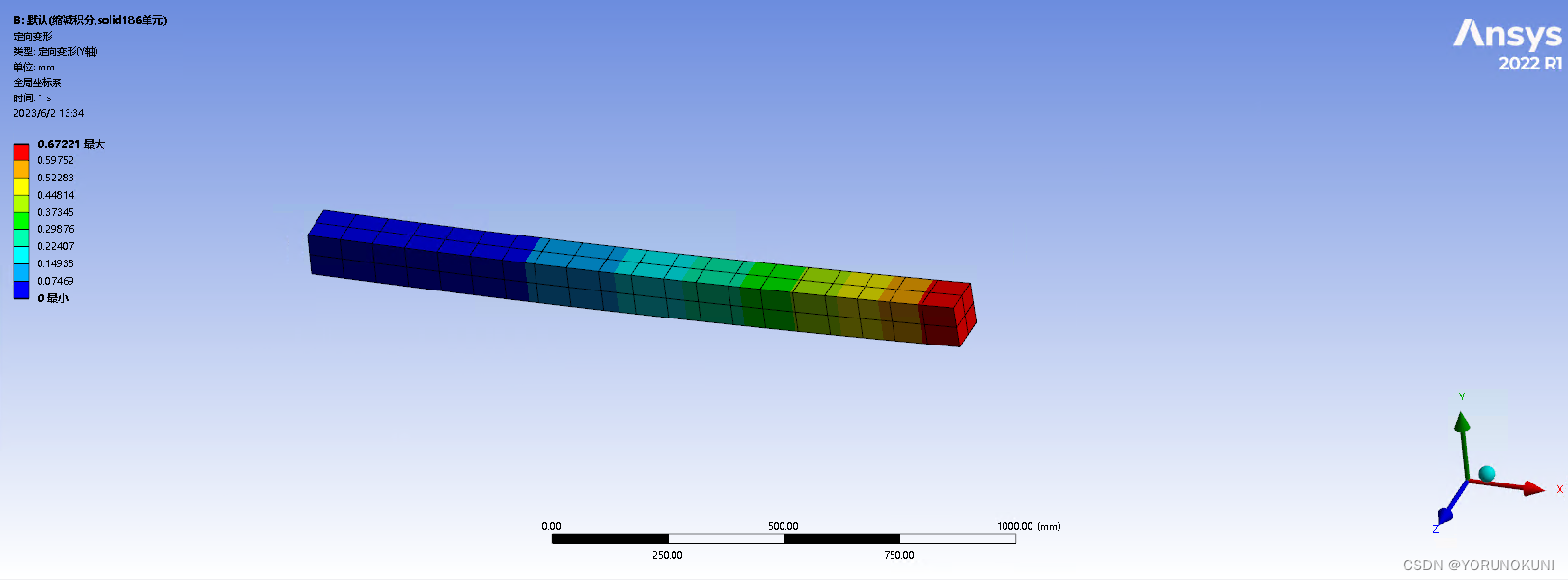 图3.5a 186单元缩减积分下变形结果
图3.5a 186单元缩减积分下变形结果
 图3.5b 186单元缩减积分下切应力结果
图3.5b 186单元缩减积分下切应力结果
实例3:使用完全积分solid185单 默认网格,查看Y轴定向变形和切应力,如下图所示。可以看出,梁的最大变形为0.592mm,与理论解的相对误差为-12.3%,此时的计算结果已经存在很大误差了。同样输出梁中间段的切应力,此时切应力的最大值为1.52MPa,可以说明当使用完全积分的低阶单元时,算例中发生了剪切自锁。 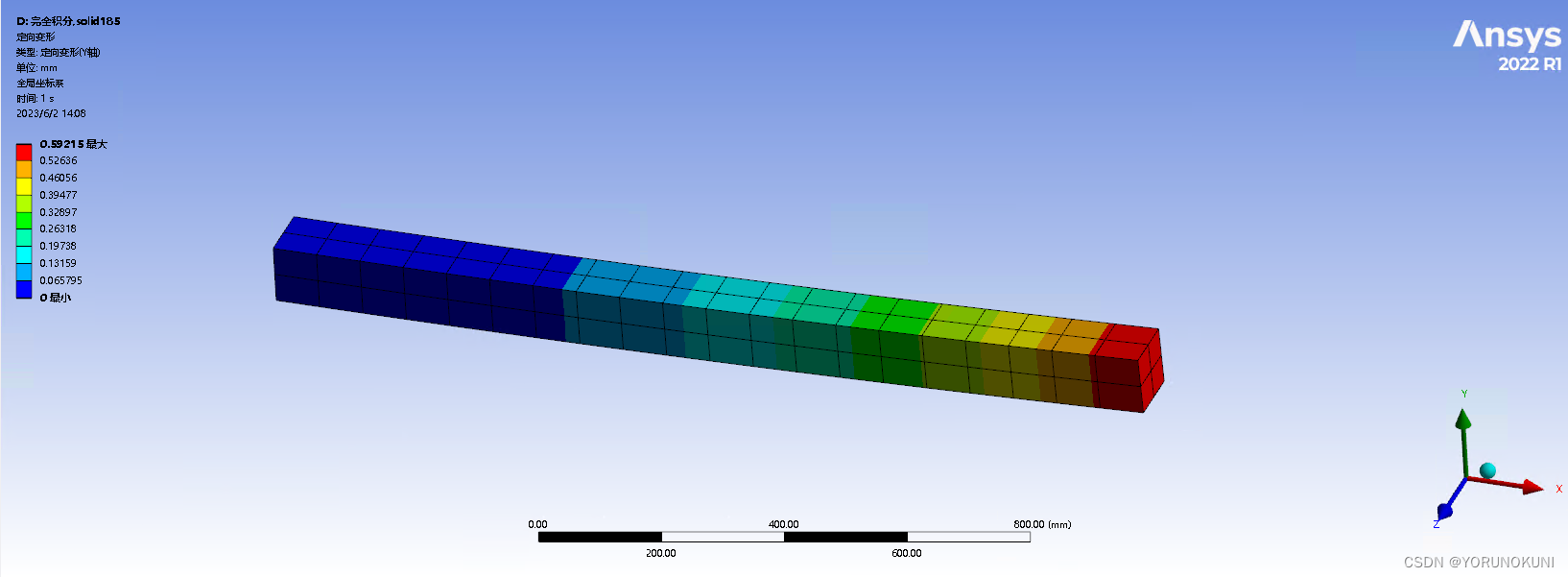 图3.6a 185单元完全积分下变形结果
图3.6a 185单元完全积分下变形结果
 图3.6b 185单元完全积分下切应力结果
3.1.3 解决方法
图3.6b 185单元完全积分下切应力结果
3.1.3 解决方法
在ANSYS APDL中针对剪切自锁问题给出了多种解决办法,如选择缩减积分,使用增强应变积分或简单增强应变积分等,这些方法可通过控制单元类型中的K2关键字进行选择。详细内容可查看ANSYS非线性部分的帮助文档。 在Workbench中为解决剪切自锁问题可采用如下办法: 1.使用高阶单元:已知剪切自锁一般发生在完全积分的低阶单元中,因此使用高阶单元可以在一定程度上消除剪切自锁现象,但由于单元节点的增加,计算量也会有相应提高。案例如下: 实例4:使用完全积分solid186单元 基于实例3,仅将185单元改为186单元,其余条件不变进行求解。从图中可以看出,使用高阶单元后最大位移值变为了0.6715mm,与理论解的相对误差为-0.52%,计算精度相较于实例3的结果有了大幅度提高,切应力的数值也大幅度减小。可见使用高阶单元可以在一定程度上消除剪切自锁现象。 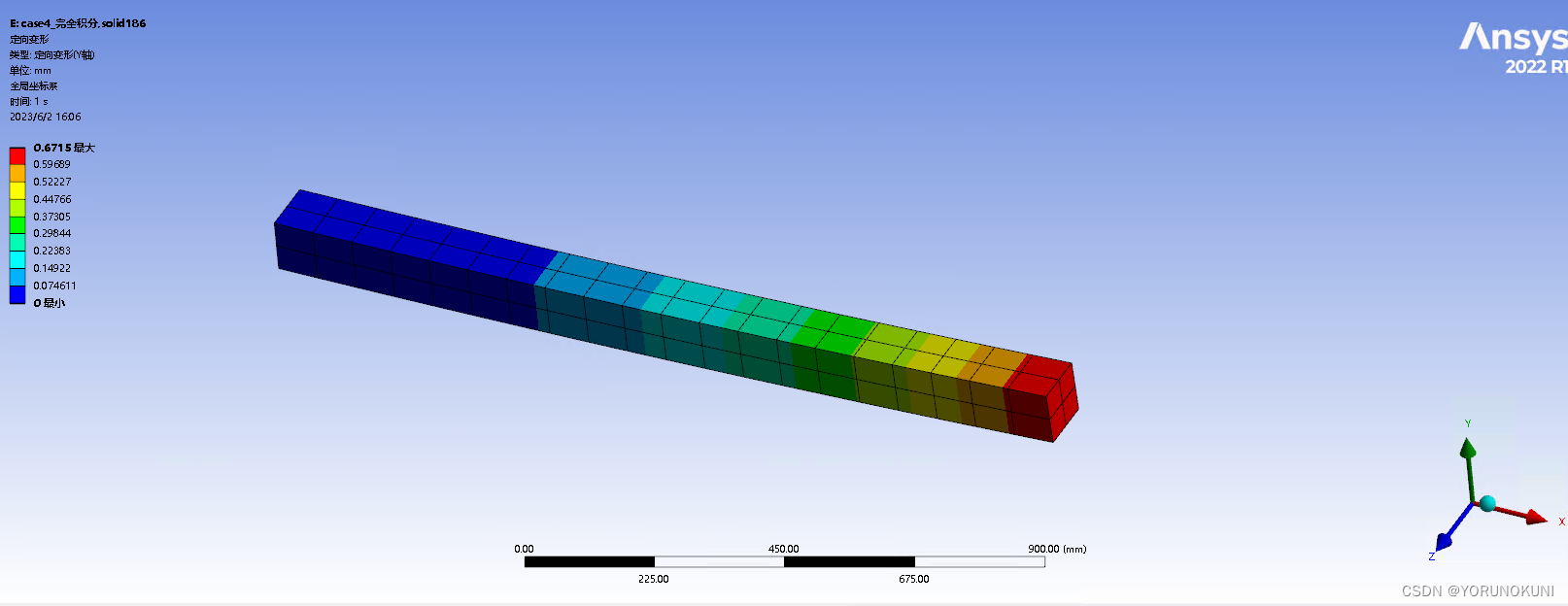 图3.7a 186单元完全积分下变形结果
图3.7a 186单元完全积分下变形结果
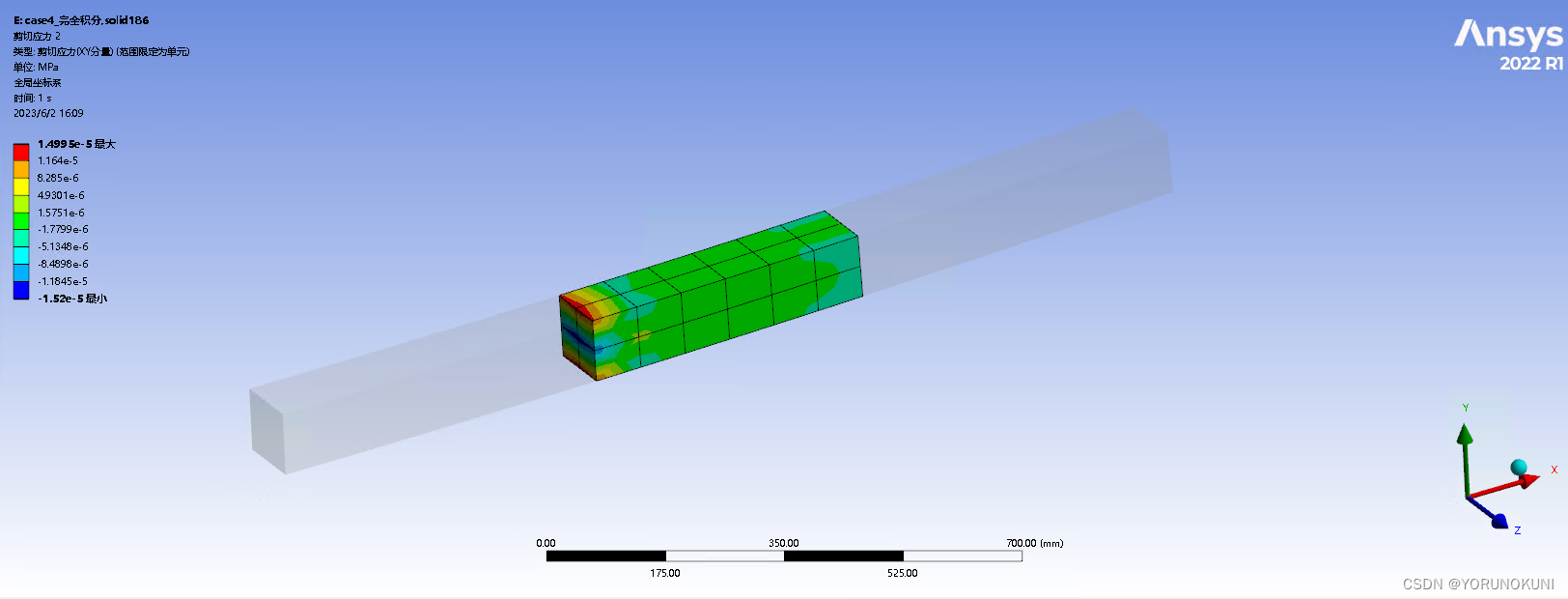 图3.7b 186单元完全积分下切应力结果
图3.7b 186单元完全积分下切应力结果
2.使用缩减积分:缩减积分可处理剪切自锁问题,但是在上文的图3.2中显示,如果对低阶单元使用缩减积分,则在单元中心只有1个积分点,因此该方法会导致零能模式。 所谓零能模式是指在只有一个积分点的低阶单元中,此积分点未获得任何单元应变能,即所有的应力分量都是零。而沙漏模式通常只是低阶缩减积分单元中的问题,如下图所示,对于单个积分点的低阶单元,如果对角线的节点产生相同的位移,则积分点位置处即中间的横线没有伸长也没有缩短,所以单元没有产生正应力,此外横线和竖线的夹角也没有变化,所以单元也没有产生切应力,单元不能承受任何载荷,刚度为零。下面看一个会出现沙漏的例子:  图3.8 沙漏模式
图3.8 沙漏模式
实例5:使用缩减积分solid185单元 基于实例3,仅将完全积分改为缩减积分,其余条件不变计算结果。从图中可以看出,使用缩减积分后最大位移值变为了0.897mm,与理论解相差较大,但是切应力的数值大幅减小。猜测应该是出现了沙漏现象,在下文将会对沙漏模式进行详述。 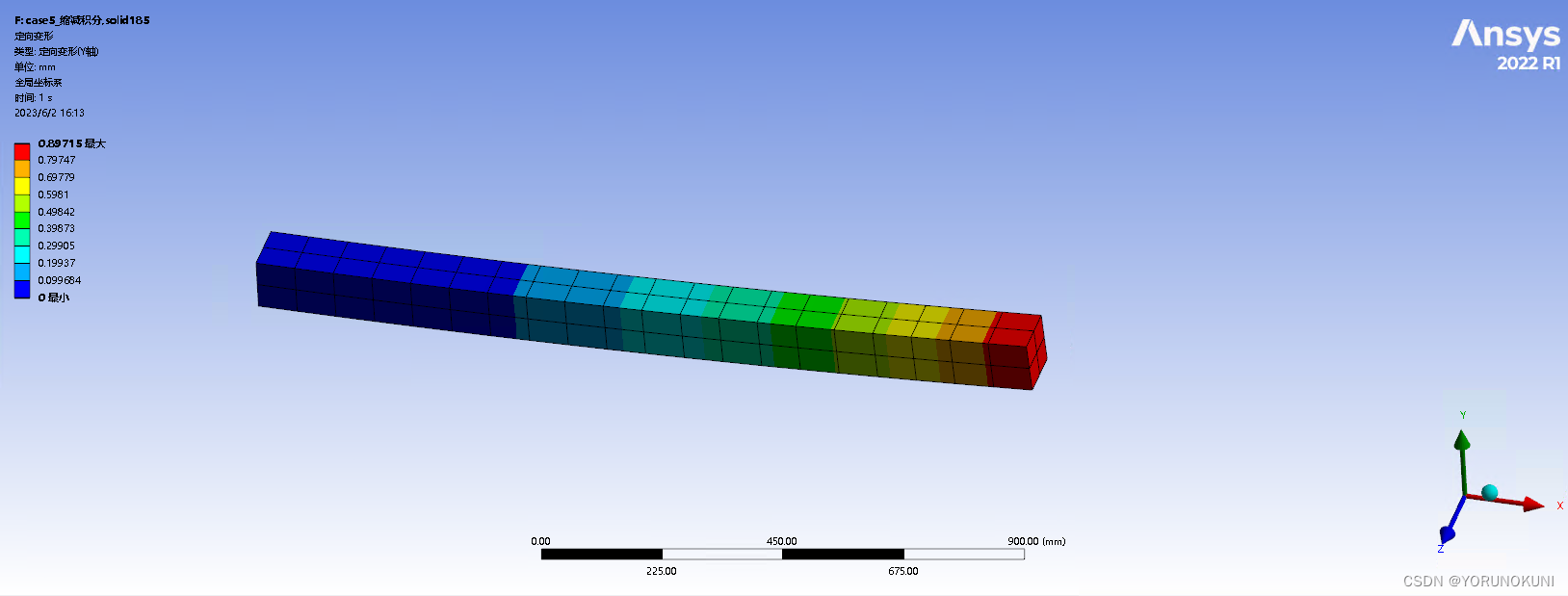 图3.9a 185单元缩减积分下变形结果
图3.9a 185单元缩减积分下变形结果
 图3.9a 185单元缩减积分下切应力结果
图3.9a 185单元缩减积分下切应力结果
3.细化网格:在此将对实例3(完全积分185)和实例5(缩减积分185)进行网格加密,加密后的结果云图可通过附件中的算例查看,在此仅使用表格统计加密后的结果数据。在实例6中对实例5进行网格加密,在实例7中对实例3进行网格加密,可以看出,随着网格密度的增加,最大位移值逐渐趋近于理论解,但是这两个模型的收敛速度却不一样。处于默认网格下实例7也存在剪切自锁,但随着网格密度的增加,计算结果快速收敛于理论值,剪切自锁现象很快消失了。处于默认网格下实例6存在沙漏效应,随着网格密度的增加,虽然计算结果也逐渐收敛于理论解,但是收敛速度相较于实例7要慢很多。可见,为缓解沙漏造成的计算误差,需要较大的网格量。 表3.1 细化网格后的结果数据 网格/mm实例6位移/mm误差实例7位移/mm误差75(默认)0.89732.89%0.592-12.30%500.89732.89%0.662-1.93%300.7186.37%0.662-1.93%200.7024.00%0.67-0.74%100.680.74%0.672-0.44% 3.2 沙漏模式在上文的缩减积分中已经对沙漏模式进行了详细描述,如果把剪切自锁称为“刚度过硬”现象,那么沙漏模式可以理解为“刚度过软”。沙漏模式出现于缩减积分的情况下,通常只是低阶单元中的问题,只要在每个方向上有多于一个的单元,高阶缩减积分单元的零能模式就不会传播。在此用实例5的模型观察沙漏的产生与解决方法。 3.2.1 实例实例8:改变实例5的网格验证沙漏模式 在模态分析中,刚度对结果的影响很大,因此使用模态分析对沙漏效应进行描述。在实例5后建立预应力模态分析,计算前6阶固有频率。由于该算例出现了沙漏效应,所以计算出的固有频率要小于实际。已知在实例1下,第1阶模态频率为36.112Hz。从图中可以看出,实例5的第1阶固有频率为31.345Hz,确实要小于实例1的结果。 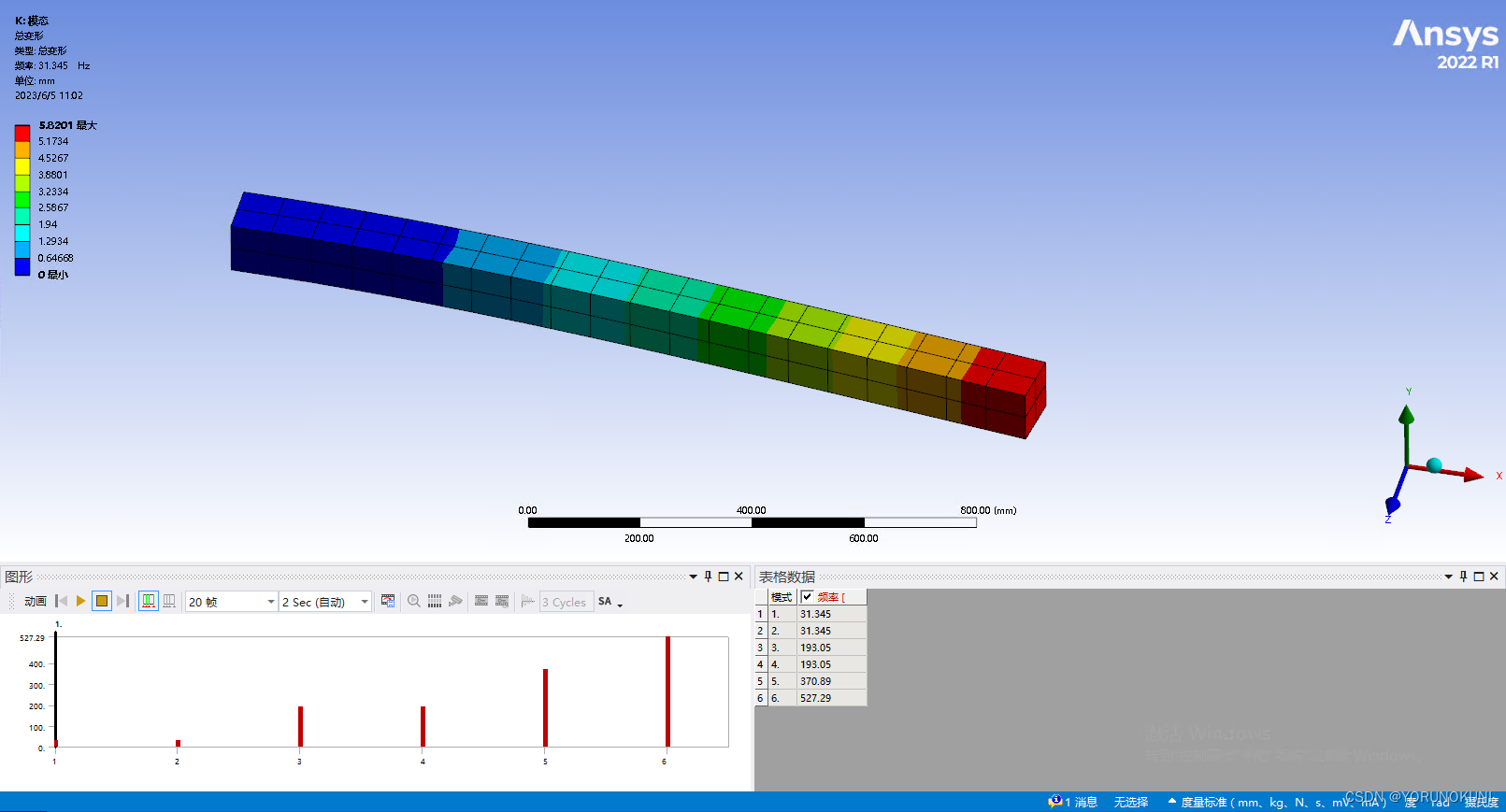 图3.10 沙漏模式下的固有频率
图3.10 沙漏模式下的固有频率
为了使沙漏效应更加明显,将全局网格尺寸改为100mm,重新计算结构的变形和模态,结果如下所示。网格稀疏后沙漏效应进一步放大,由于结构刚度变小导致变形大幅增加,最大位移值为119mm,变形已经非常夸张了,与此同时第1阶固有频率变为了2.742Hz,出现了大幅减小。大家可以通过修改实例9中的网格参数进行验证。 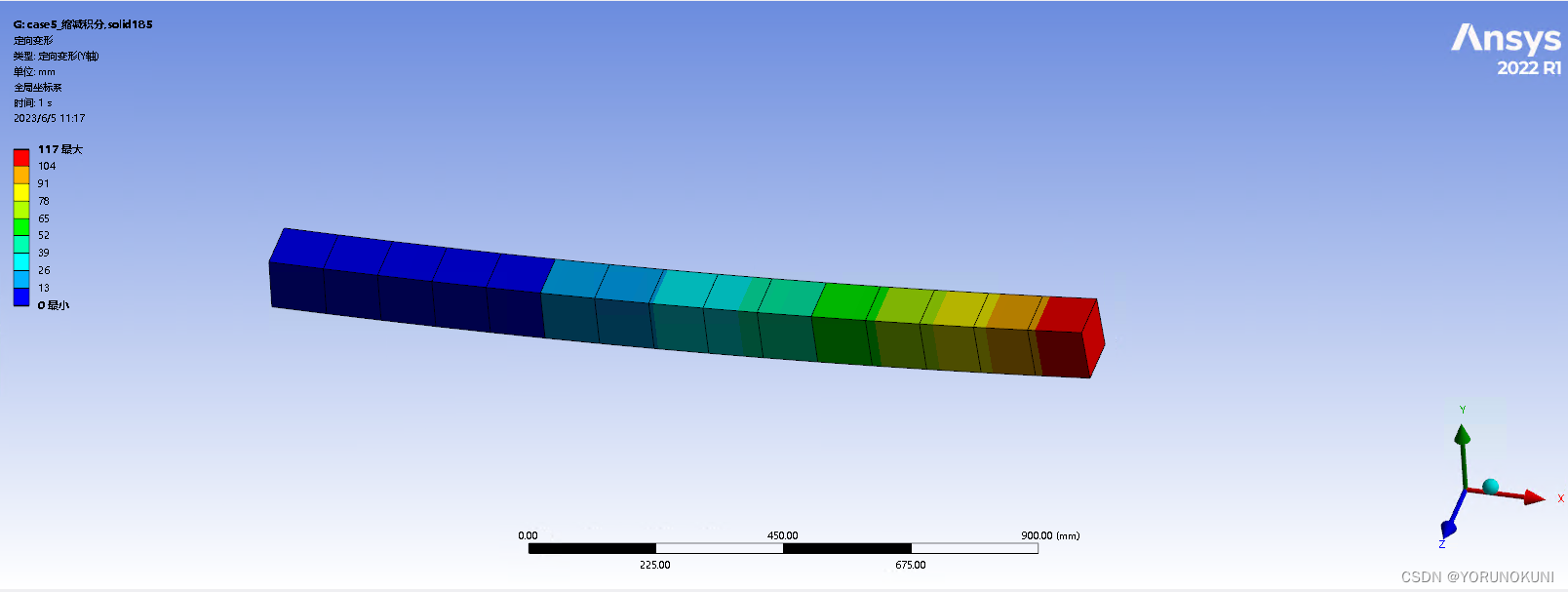 图3.11a 减少网格后的变形结果
图3.11a 减少网格后的变形结果
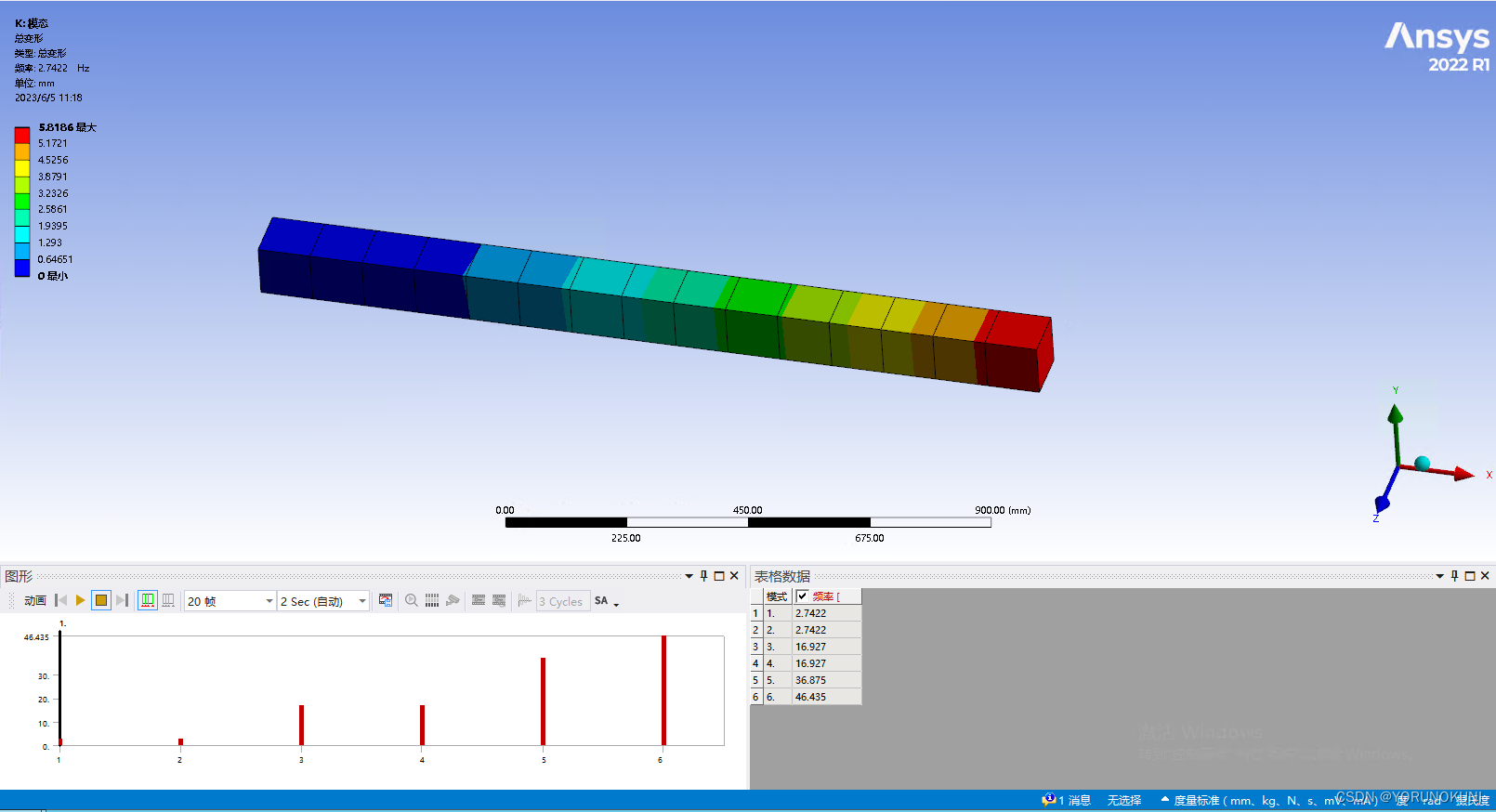 图3.11b 减少网格后的固有频率
图3.11b 减少网格后的固有频率
若将实例5中的网格设为高阶单元(即缩减积分186单元—实例2),则计算结果与36.112Hz非常接近;若将实例5中的积分方式变为完全积分(即完全积分185单元——实例3),则计算结果要大于36.112Hz,因为此时结构发生了剪切自锁,刚度变大了,大家可自行验证。 3.2.2 解决方法沙漏模式可以通过细化网格得到解决,在缩减积分时低阶单元只有一个积分点,所以也要避免使用点载荷,同时在大应变区域或大应变梯度区域使用线性单元。上述沙漏效应可以通过细化网格得到解决,大家可自行验证。 3.3 体积自锁体积自锁问题常发生于不可压缩材料的计算过程中,若使用完全积分单元则会造成体积自锁,与剪切自锁相似,此时单元中产生的伪压应力导致单元不会发生任何变形,出现“刚度过硬”。体积自锁问题同样可以通过细化网格得到解决,相关案例在后续会进行补充...... 附录剪切自锁:实例1-7 沙漏模式:实例8 |
【本文地址】