| 回归模型常见的损失函数 | 您所在的位置:网站首页 › 回归模型公式有哪些 › 回归模型常见的损失函数 |
回归模型常见的损失函数
|
注意:如果图片不显示,请建议科学上网或者使用VPN。 机器学习中的所有算法都依赖于最小化或最大化函数,我们将其称为“目标函数”。最小化的函数组称为“损失函数”。损失函数是衡量预测模型在能够预测预期结果方面的表现有多好的指标。寻找最小值的最常用方法是“梯度下降”。想想这个函数的作用,如起伏的山脉和梯度下降就像滑下山到达最低点。 没有一种损失函数适用于所有类型的数据。它取决于许多因素,包括异常值的存在,机器学习算法的选择,梯度下降的时间效率,易于找到衍生物和预测的置信度。 损失函数可大致分为两类:分类和回归损失。在这篇文章中,专注于讨论回归损失函数。
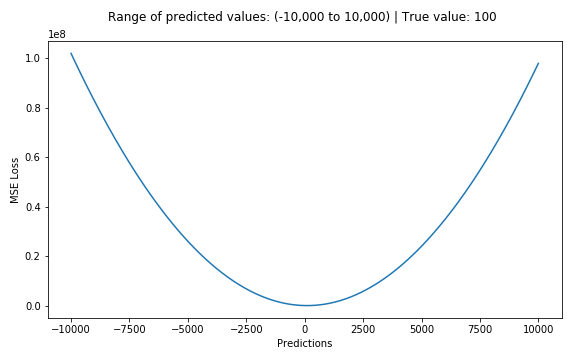
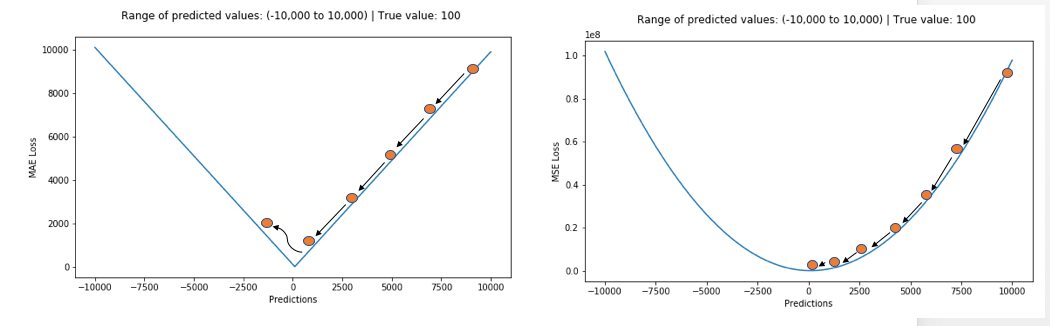
均方误差(MSE)(又称二次损失,L2损失)是最常用的回归损失函数。MSE是目标变量和预测值之间的平方距离之和。 M S E = ∑ i = 1 n ( y i − y i p ) 2 n M S E=\frac{\sum_{i=1}^{n}\left(y_{i}-y_{i}^{p}\right)^{2}}{n} MSE=n∑i=1n(yi−yip)2 下面是MSE函数的图,其中真实目标值为100,预测值范围在-10,000到10,000之间。MSE损失(Y轴)在预测(X轴)= 100时达到其最小值。其范围是0到∞。
MSE损失(Y轴)与预测(X轴)的关系图 2. 平均绝对误差平均绝对误差(MAE)(又称L1损失)是用于回归模型的另一种损失函数。MAE是我们的目标和预测变量之间的绝对差异的总和。因此,它在不考虑方向的情况下测量一组预测中的平均误差大小。(如果我们也考虑方向,那将被称为平均偏差误差(MBE),它是残差/误差的总和)。其范围也是0到∞。
M
A
E
=
∑
i
=
1
n
∣
y
i
−
y
i
p
∣
n
M A E=\frac{\sum_{i=1}^{n}\left|y_{i}-y_{i}^{p}\right|}{n}
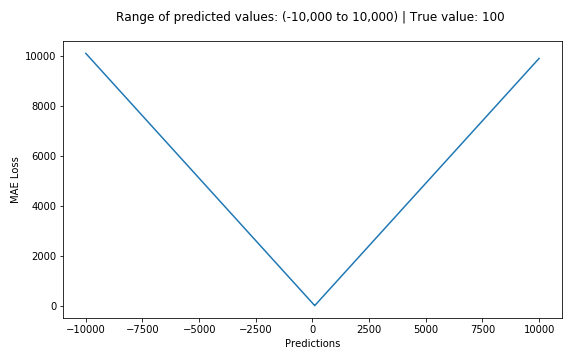
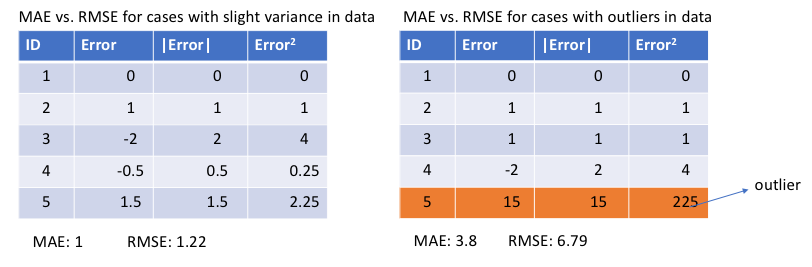
MAE=n∑i=1n∣yi−yip∣ MAE损失(Y轴)与预测(X轴)的关系图 MSE与MAE(L2损失与L1损失) 简而言之, 使用平方误差更容易解决,但使用绝对误差对异常值更为稳健。但是让我们明白为什么! 每当我们训练机器学习模型时,我们的目标是找到最小化损失函数的点。当然,当预测完全等于真实值时,两个函数都达到最小值。 这里是两个python代码的快速回顾。 import numpy as np #true:真实目标变量的数组 #prep:预测数组 def mse(true,pred): return np.sum((true - pred)** 2) def mae(true,pred): return np.sum(np.abs(true - pred))让我们看看MAE和均方根误差的值(RMSE,它只是MSE的平方根,使其与MAE的比例相同)。在第一种情况下,预测接近真实值,并且误差在观察值之间具有小的差异。在第二个,有一个异常值观察,误差很高。
我们从中观察到了什么,它如何帮助我们选择使用哪种损失函数? 由于MSE平方误差(y-y_predicted = e),如果e> 1,则误差(e)的值会增加很多。如果我们的数据中有异常值,则e的值将为高,e²将为>> | E |。这将使具有MSE损失的模型比具有MAE损失的模型对异常值更敏感。在上面的第二种情况中,将调整RMSE作为损失的模型,以便以牺牲其他常见示例为代价来最小化单个异常情况,这将降低其整体性能。 如果训练数据被异常值破坏(即我们在训练环境中存在错误较大的正值或负值,而不是我们的测试环境),则MAE损失很有用。 直观地说,我们可以考虑一下这样的:如果我们只给一个预测为所有尽量减少MSE的意见,那么预测应该是所有目标值的均值。但是,如果我们试图最小化MAE,那么预测将是所有观测的中位数。我们知道,中值对异常值的影响比均值更强,因此使用MAE对异常值处理效果要比MSE更好。 使用MAE损失(尤其是神经网络)的一个大问题是它的梯度始终是相同的,这意味着即使对于小的损耗值,梯度也会很大。这对学习不利。为了解决这个问题,我们可以使用随着我们接近最小值而降低的动态学习率。在这种情况下,MSE表现良好,即使具有固定的学习速率也会收敛。MSE损失的梯度对于较大的损失值是高的,并且随着损失接近0而降低,使其在训练结束时更精确(见下图)。
决定使用哪种损失函数如果异常值表示对业务很重要且应该检测到的异常,那么我们应该使用MSE。另一方面,如果我们认为异常值只表示损坏的数据,那么我们应该选择MAE作为损失。 我建议阅读这篇文章,并进行一项很好的研究,比较在有异常值存在和不存在的情况下使用L1损失和L2损失的回归模型的性能。请记住,L1和L2损失只是MAE和MSE的另一个名称。 L1损失对异常值更为稳健,但其衍生物不连续,使得找到解决方案效率低下。L2损失对异常值敏感,但提供更稳定和封闭的形式解决方案(通过将其导数设置为0)。 **两者都有问题:**可能存在损失函数都没有给出理想预测的情况。例如,如果我们数据中90%的观察值具有150的真实目标值,则剩余的10%具有0-30之间的目标值。然后,MAE作为损失的模型可能预测所有观察值为150,忽略10%的离群值情况,因为它将试图达到中值。在相同的情况下,使用MSE的模型会给出0到30范围内的许多预测,因为它会偏向异常值。 **在这种情况下该怎么办?**一个简单的解决方法是转换目标变量。另一种方法是尝试不同的损失功能。这是我们的第三次亏损功能背后的动机,Huber损失。 3. Huber损失Huber损失(又称平滑平均绝对误差)对数据中的异常值的敏感性低于平方误差损失。它在0处也是可微分的。它基本上是绝对误差,当误差很小时变为二次曲线。该误差必须多小才能使其成为二次方取决于可以调整的超参数δ(delta)。当δ0时,**Huber损失接近**MAE,当δ∞(大数)时, Huber损耗接近MSE。
L
δ
(
y
,
f
(
x
)
)
=
{
1
2
(
y
−
f
(
x
)
)
2
for
∣
y
−
f
(
x
)
∣
≤
δ
δ
∣
y
−
f
(
x
)
∣
−
1
2
δ
2
otherwise
L_{\delta}(y, f(x))=\left\{\begin{array}{ll}{\frac{1}{2}(y-f(x))^{2}} ; {\text { for }|y-f(x)| \leq \delta} \\ {\delta|y-f(x)|-\frac{1}{2} \delta^{2}} ; {\text { otherwise }}\end{array}\right.
Lδ(y,f(x))={21(y−f(x))2δ∣y−f(x)∣−21δ2 for ∣y−f(x)∣≤δ otherwise δ的选择至关重要,因为它决定了你愿意考虑的异常值。大于δ的残差最小化为L1(对大异常值不敏感),而小于δ的残差最小化为“适当”L2。 **为什么要使用Huber Loss?**使用MAE训练神经网络的一个大问题是其持续的大梯度,这可能导致在训练结束时使用梯度下降丢失最小值。对于MSE,随着损失接近其最小值,梯度减小,使其更精确。 在这种情况下,胡贝尔损失确实很有用,因为它在最小值附近弯曲,从而降低了梯度。而且它比MSE更强大。因此,它结合了MSE和MAE的良好特性。然而,Huber损失的问题是我们可能需要训练超参数δ,这是一个迭代过程。 4. Log-Cosh损失Log-cosh是回归任务中使用的另一个函数,比L2更平滑。Log-cosh是预测误差的双曲余弦的对数。
L
(
y
,
y
p
)
=
∑
i
=
1
n
log
(
cosh
(
y
i
p
−
y
i
)
)
L\left(y, y^{p}\right)=\sum_{i=1}^{n} \log \left(\cosh \left(y_{i}^{p}-y_{i}\right)\right)
L(y,yp)=i=1∑nlog(cosh(yip−yi)) **优点:**当x值较小 时,log(cosh(x))约等于(x ** 2) / 2;当x值较大时,约等于abs(x) - log(2)。这意味着’logcosh’的作用大部分类似于均方误差,但不会受到偶然误差预测的强烈影响。它具有Huber损失的所有优点,并且它在各处都是可区分的,与Huber损失不同。 **为什么我们需要二阶导数?**像XGBoost这样的许多ML模型实现使用牛顿方法来找到最优,这就是为什么需要二阶导数(Hessian)。对于像XGBoost这样的ML框架,两个可区分的函数更有利。
XgBoost中使用的目标函数。注意对1阶和2阶导数的依赖性 但Log-cosh损失并不完美。对于非常大的脱靶预测是恒定的,它仍然存在梯度和粗麻布的问题,因此导致没有XGBoost的分裂。 Huber和Log-cosh损失函数的Python代码: # huber loss def huber(true, pred, delta): loss = np.where(np.abs(true-pred) |
【本文地址】
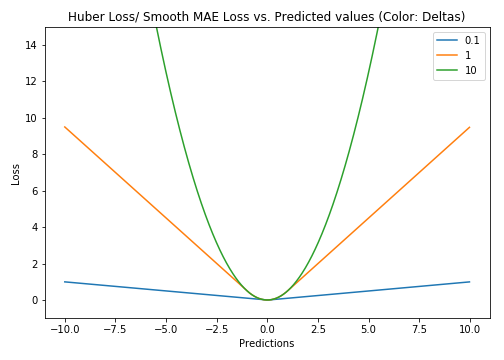 Hoss损失(Y轴)与预测(X轴)的关系图。
Hoss损失(Y轴)与预测(X轴)的关系图。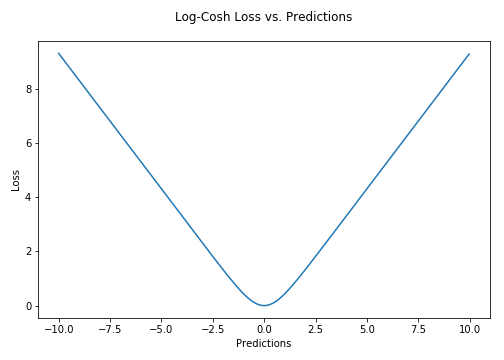 Log-cosh Loss(Y轴)与预测(X轴)的关系图。
Log-cosh Loss(Y轴)与预测(X轴)的关系图。