| 6.3 平面向量的基本定理及坐标表示 | 您所在的位置:网站首页 › 向量a的表示方式 › 6.3 平面向量的基本定理及坐标表示 |
6.3 平面向量的基本定理及坐标表示
|
\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\) 【高分突破系列】数学下学期同步知识点剖析精品讲义! \(\mathbf{{\large {{\color{Red} {跟贵哥学数学,so \quad easy!}} }}}\) 必修第二册同步拔高,难度3颗星! 模块导图 知识剖析
平面向量的基本定理
知识剖析
平面向量的基本定理
1 平面向量的基本定理
设\(\overrightarrow{e_{1}}\),\(\overrightarrow{e_{2}}\)同一平面内的两个不共线向量, \(\vec{a}\)是该平面内任一向量,则存在唯一实数对$ (λ,μ)$,使 \(\vec{a}=\lambda \overrightarrow{e_{1}}+\mu \overrightarrow{e_{2}}\).
我们把\(\{\vec{e_1},\vec{e_2}\}\)叫做表示这个平面内所有向量的一个基底.
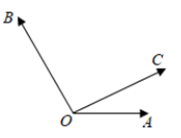
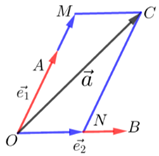
如下图,\(\vec{a}=\overrightarrow{O M}+\overrightarrow{O N}=\lambda \overrightarrow{e_{1}}+\mu \overrightarrow{e_{2}}\),其中\(\lambda=\dfrac{|O M|}{|O A|}\),\(\mu=\dfrac{|O N|}{|O B|}\).
2 正交分解及其坐标表示
① 正交分解
把一个向量分解为两个互相垂直的向量,叫做把向量作正交分解;
② 向量的坐标表示 在平面内建立直角坐标系,以与\(x\)轴、\(y\)轴方向相同的两个单位向量\(\vec{i}\) ,\(\vec{j}\)为基底,则平面内的任一向量\(\vec{a}\)表示为\(\vec{a}=x \vec{i}+y \vec{j}=(x, y)\),\((x ,y)\)称为向量\(\vec{a}\)的坐标,\(\vec{a}=(x, y)\)叫做向量\(\vec{a}\)的坐标表示. 向量\(\vec{a}=(x, y)\),就是以原点\((0,0)\)为起点,点\((x ,y)\)为终点的向量. 平面向量数乘运算与数量积的坐标表示1 坐标运算
设\(\vec{a}=\left(x_{1}, y_{1}\right)\) ,\(\vec{b}=\left(x_{2}, y_{2}\right)\),则
\((1)\)向量的模\(|\vec{a}|=\sqrt{x_{1}^{2}+y_{1}^{2}}\)
\((2)\)向量的加减法运算 \(\vec{a}+\vec{b}=\left(x_{1}+x_{2}, y_{1}+y_{2}\right)\),\(\vec{a}-\vec{b}=\left(x_{1}-x_{2}, y_{1}-y_{2}\right)\)
\((3)\)若\(A(x_1 ,y_1)\),\(B(x_2 ,y_2)\),则\(\overrightarrow{A B}=\left(x_{2}-x_{1}, y_{2}-y_{1}\right)\)
\((4)\)实数与向量的积 \(\lambda \vec{a}=\lambda\left(x_{1}, y_{1}\right)=\left(\lambda x_{1}, \lambda y_{1}\right)\)
\((5)\)数量积\(\vec{a} \cdot \vec{b}=x_{1} x_{2}+y_{1} y_{2}\)
\((6)\)夹角余弦值\(\cos =\dfrac{\vec{a} \cdot \vec{b}}{|\vec{a}| \vec{b} \mid}=\dfrac{x_{1} x_{2}+y_{1} y_{2}}{\sqrt{x_{1}^{2}+y_{1}^{2}} \cdot \sqrt{x_{2}^{2}+y_{2}^{2}}}\)
\({\color{Red}{拓展}}\) 定比分点
线段\(P_1P_2\)的端点\(P_1\)、\(P_2\)的坐标分别是\((x_1 ,y_1)\),\((x_2 ,y_2)\),点\(P\)是直线\(P_1 P_2\)上的一点,
当\(\overrightarrow{P_{1} P}=\lambda \overrightarrow{P P_{2}}\)时,点\(P\)的坐标是\(\left(\dfrac{x_{1}+\lambda x_{2}}{1+\lambda}, \dfrac{y_{1}+\lambda y_{2}}{1+\lambda}\right)\)
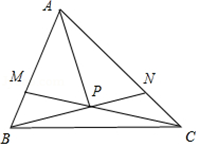
2 平面向量位置关系 若\(\vec{a}\left(x_{1}, y_{1}\right)\),\(\vec{b}\left(x_{2}, y_{2}\right)\), \(\vec{a} \| \vec{b} \Leftrightarrow x_{1} y_{2}=x_{2} y_{1}\), \(\vec{a} \perp \vec{b} \Rightarrow \vec{a} \cdot \vec{b}=0 \Rightarrow x_{1} x_{2}+y_{1} y_{2}=0\). 经典例题 【题型一】平面向量的基本定理的理解【典题1】 如果\(\overrightarrow{e_{1}}\),\(\overrightarrow{e_{2}}\)是平面内一组不共线的向量,那么下列四组向量中,不能作为平面内所有向量的一组基底的是( ) A.\(\overrightarrow{e_{1}}\)与\(\overrightarrow{e_{1}}+\overrightarrow{e_{2}}\) B.\(\overrightarrow{e_{1}}-2 \overrightarrow{e_{2}}\)与\(\overrightarrow{e_{1}}+2 \overrightarrow{e_{2}}\) C.\(\overrightarrow{e_{1}}+\overrightarrow{e_{2}}\)与\(\overrightarrow{e_{1}}-\overrightarrow{e_{2}}\) D.\(\overrightarrow{e_{1}}-2 \overrightarrow{e_{2}}\)与\(-\overrightarrow{e_{1}}+2 \overrightarrow{e_{2}}\) 【解析】\(\overrightarrow{e_{1}}\),\(\overrightarrow{e_{2}}\)是平面内一组不共线的向量,作为基底的向量,前提为不共线向量,所以对于选项\(ABC\)都为不共线向量,选项\(D\) \(\overrightarrow{e_{1}}-2 \overrightarrow{e_{2}}\)与\(-\overrightarrow{e_{1}}+2 \overrightarrow{e_{2}}\)为共线向量. 故选 \(D\). 【典题2】已知方程\(\vec{a} x^{2}+\vec{b} x+\vec{c}=0\),其中\(\vec{a}\),\(\vec{b}\),\(\vec{c}\)是非零向量,且\(\vec{a}\),\(\vec{b}\)不共线,则该方程( ) A.至多有一个解 \(\qquad \qquad \qquad \qquad\) B.至少有一个解 C.至多有两个解 \(\qquad \qquad \qquad \qquad\) D.可能有无数多个解 【解析】\(∵\vec{a} x^{2}+\vec{b} x+\vec{c}=0\),\(\therefore \vec{c}=-\vec{a} x^{2}-\vec{b} x\), \(∵\vec{a}\),\(\vec{b}\)不共线, 故存在唯一一对实数\(λ ,μ\)使\(\vec{c}=\lambda \vec{a}+\mu \vec{b}\) 若\(λ\)满足\(λ=-μ^2\),则方程有一个解; \(λ\)不满足\(λ=-μ^2\),则方程无解;所以至多一个解, 故选 \(A\). 【点拨】本题考核对平面向量的基本定理中的”存在性、唯一性”的理解. 【题型二】平面向量的基本定理的运用 【典题1】已知在\(△ABC\)中,\(M ,N\)分别是边\(AB\),\(AC\)上的点,且\(\overrightarrow{A M}=2 \overrightarrow{M B}\),\(\overrightarrow{A N}=3 \overrightarrow{N C}\),\(BN\)与\(CM\)相交于点\(P\) , 记\(\vec{a}=\overrightarrow{A B}\),\(\vec{b}=\overrightarrow{A C}\),用\(\vec{a}, \quad \vec{b}\)表示\(\overrightarrow{A P}\)的结果是( )
A.\(\overrightarrow{A P}=\dfrac{1}{3} \vec{a}+\dfrac{2}{3} \vec{b}\)
B.\(\overrightarrow{A P}=\dfrac{1}{2} \vec{a}+\dfrac{1}{3} \vec{b}\)
C.\(\overrightarrow{A P}=\dfrac{2}{5} \vec{a}+\dfrac{1}{3} \vec{b}\)
D.\(\overrightarrow{A P}=\dfrac{1}{3} \vec{a}+\dfrac{1}{2} \vec{b}\)
【解析】 由题意,可知\(\overrightarrow{A M}=\dfrac{2}{3} \overrightarrow{A B}\),\(\overrightarrow{A N}=\dfrac{3}{4} \overrightarrow{A C}\) 设\(\overrightarrow{B P}=\lambda \overrightarrow{B N}\), 则有\(\overrightarrow{A P}=\overrightarrow{A B}+\overrightarrow{B P}=\overrightarrow{A B}+\lambda \overrightarrow{B N}\)\(=\overrightarrow{A B}+\lambda(\overrightarrow{A N}-\overrightarrow{A B})\) \(=\overrightarrow{A B}+\lambda \overrightarrow{A N}-\lambda \overrightarrow{A B}\)\(=(1-\lambda) \overrightarrow{A B}+\lambda \cdot \dfrac{3}{4} \overrightarrow{A C}\)\(=(1-\lambda) \vec{a}+\dfrac{3}{4} \lambda \vec{b}\) ① 又设\(\overrightarrow{C P}=\mu \overrightarrow{C M}\), 则有\(\overrightarrow{A P}=\overrightarrow{A C}+\overrightarrow{C P}=\overrightarrow{A C}+\mu \overrightarrow{C M}\)\(=\overrightarrow{A C}+\mu(\overrightarrow{A M}-\overrightarrow{A C})\)\(=\overrightarrow{A C}+\mu \overrightarrow{A M}-\mu \overrightarrow{A C}\) \(=(1-\mu) \overrightarrow{A C}+\mu \cdot \dfrac{2}{3} \overrightarrow{A B}\)\(=\dfrac{2}{3} \mu \vec{a}+(1-\mu) \vec{b}\) ② 通过比较①②,可得关于\(λ ,μ\)的二元一次方程组:\(\left\{\begin{array}{l} 1-\lambda=\dfrac{2}{3} \mu \\ \dfrac{3}{4} \lambda=1-\mu \end{array}\right.\), 解此二元一次方程组,得\(\left\{\begin{array}{l} \lambda=\dfrac{2}{3} \\ \mu=\dfrac{1}{2} \end{array}\right.\), 将结果带入①式,可得\(\overrightarrow{A P}=\dfrac{1}{3} \vec{a}+\dfrac{1}{2} \vec{b}\),故选:\(D\). 【点拨】 ① 这里给到的方法是以不共线向量\(\vec{a}, \vec{b}\)为基底,通过两个方式得到向量\(\overrightarrow{A P}\)的表达式,即\((1-\lambda) \vec{a}+\dfrac{3}{4} \lambda \vec{b}=\dfrac{2}{3} \mu \vec{a}+(1-\mu) \vec{b}\),再由平面向量的基本定理求出\(\overrightarrow{A P}\). ② 本题方法很多也可以用平行四边形法则求解. 【典题2】 如图,两块斜边长相等的直角三角板拼在一起.若\(\overrightarrow{A D}=x \overrightarrow{A B}+y \overrightarrow{A C}\),求\(x ,y\).
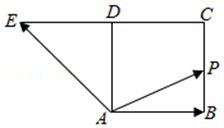
【典题3】 在直角梯形\(ABCD\)中,\(AB⊥AD\),\(AD∥BC\),\(AB=BC=2AD=2\),\(E\),\(F\)分别为\(BC\),\(CD\)的中点,以\(A\)为圆心,\(AD\)为半径的半圆分别交\(BA\)及其延长线于点\(M\),\(N\),点\(P\)在\(\widehat{M D N}\)上运动(如图).若\(\overrightarrow{A P}=\lambda \overrightarrow{A E}+\mu \overrightarrow{B F}\),其中\(λ ,μ∈R\),则\(2λ-5μ\)的取值范围是\(\underline{\quad \quad}\).
1(★) 下列各组向量中,可以作为基底的是( ) A.\(\overrightarrow{e_{1}}=(0,0), \overrightarrow{e_{2}}=(1,2)\) B.\(\overrightarrow{e_{1}}=(-1,2), \overrightarrow{e_{2}}=(5,7)\) C.\(\overrightarrow{e_{1}}=(3,5), \overrightarrow{e_{2}}=(6,10)\) D.\(\overrightarrow{e_{1}}=(2,-3), \overrightarrow{e_{2}}=(-6,9)\)
2 (★★) 如图,四边形\(ABCD\)是正方形,延长\(CD\)至\(E\),使得\(DE=CD\).若动点\(P\)从点A出发,沿正方形的边按逆时针方向运动一周回到\(A\)点,其中\(\overrightarrow{A P}=\lambda \overrightarrow{A B}+\mu \overrightarrow{A E}\),下列判断正确的是( )
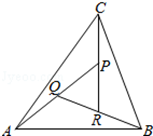
3 (★★)如图,在\(△ABC\)中,设\(\overrightarrow{A B}=\vec{a}\),\(\overrightarrow{A C}=\vec{b}\),\(AP\)的中点为\(Q\),\(BQ\)的中点为\(R\),\(CR\)的中点为\(P\),若\(\overrightarrow{A P}=m \vec{a}+n \vec{b}\),则\(m、n\)对应的值为\(\underline{\quad \quad}\).
4 (★★)如图,已知\(|\overrightarrow{O A}|=|\overrightarrow{O B}|=1\),\(|\overrightarrow{O C}|=\sqrt{3}\),\(\overrightarrow{O C} \perp \overrightarrow{O B}\),\(\langle\overrightarrow{O A}, \overrightarrow{O C}\rangle=30^{\circ}\),若\(\overrightarrow{O C}=x \overrightarrow{O A}+y \overrightarrow{O B}\),则\(x+y=\)\(\underline{\quad \quad}\).
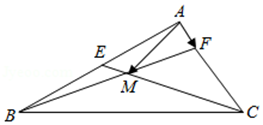
5(★★★) 在平面向量中有如下定理:设点\(O\)、\(P\)、\(Q\)、\(R\)为同一平面内的点,则\(P\)、\(Q\)、\(R\)三点共线的充要条件是:存在实数\(t\),使\(\overrightarrow{O P}=(1-t) \overrightarrow{O Q}+t \overrightarrow{O R}\).试利用该定理解答下列问题:如图,在\(△ABC\)中,点\(E\)为\(AB\)边的中点,点\(F\)在\(AC\)边上,且\(CF=2FA\),\(BF\)交\(CE\)于点\(M\),设\(\overrightarrow{A M}=x \overrightarrow{A E}+y \overrightarrow{A F}\),则\(x+y=\)\(\underline{\quad \quad}\).
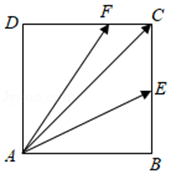
6(★★★) 在梯形\(ABCD\)中,\(\overrightarrow{A B}=2 \overrightarrow{D C}\),\(\overrightarrow{B E}=\dfrac{1}{3} \overrightarrow{B C}\),\(P\)为线段\(DE\)上的动点(包括端点),且\(\overrightarrow{A P}=\lambda \overrightarrow{A B}+\mu \overrightarrow{B C}\)\((\lambda, \mu \in \boldsymbol{R})\),则\(λ^2+μ\)的最小值为\(\underline{\quad \quad}\). 7(★★★)如图,正方形\(ABCD\)的边长为\(2\),\(E\) ,\(F\)分别为\(BC\),\(CD\)的动点,且\(|BE|=2|CF|\),设\(\overrightarrow{A C}=x \overrightarrow{A E}+y \overrightarrow{A F}\)\((x, y \in R)\),则\(x+y\)的最大值是\(\underline{\quad \quad}\).
8(★★★)如图,在平面四边形\(ABCD\)中,\(∠CBA=∠CAD=90°\),\(∠ACD=30°\),\(AB=BC\),点\(E\)在线段\(BC\)上,且\(\overrightarrow{B C}=3 \overrightarrow{B E}\),若\(\overrightarrow{A C}=\lambda \overrightarrow{A D}+\mu \overrightarrow{A E}\)\((\lambda, \mu \in \boldsymbol{R})\),则\(\dfrac{\mu}{\lambda}\)的值为\(\underline{\quad \quad}\).
【典题1】 已知平面内三向量\(\vec{a}=(2,1)\),\(\vec{b}=(-1,3)\),\(\vec{c}=(-2,2)\) (1)求满足\(\vec{a}=m \vec{b}+n \vec{c}\)的实数\(m ,n\); (2)若\((2 \vec{a}+k \vec{c} \|(\vec{b}+\vec{c})\),求实数\(k\)的值; (3)若\((2 \vec{a}+k \vec{c}) \perp(\vec{b}+\vec{c})\),求实数\(k\)的值. 【解析】 (1) \(m \vec{b}+n \vec{c}=m(-1,3)+n(-2,2)\)\(=(-m-2 n, 3 m+2 n)=(2,1)\), \(\therefore\left\{\begin{array}{l} -m-2 n=2 \\ 3 m+2 n=1 \end{array}\right.\),解得\(m=\dfrac{3}{2}\),\(n=-\dfrac{7}{4}\). (2) \(2 \vec{a}+k \vec{c}=2(2,1)+k(-2,2)=(4-2 k, 2+2 k)\), \(\vec{b}+\vec{c}=(-3,5)\), \(\because(2 \vec{a}+k \vec{c}) / /(\vec{b}+\vec{c})\),\(∴5(4-2k)-(-3)(2+2k)=0\),解得\(k=\dfrac{13}{2}\). (3)\(\because(2 \vec{a}+k \vec{c}) \perp(\vec{b}+\vec{c})\),由(2)可得\(-3(4-2k)+5(2+2k)=0\). \(\therefore k=\dfrac{1}{8}\). 【典题2】 设向量\(\overrightarrow{O A}=(1,-2)\),\(\overrightarrow{O B}=(a,-1)\),\(\overrightarrow{O C}=(-b, 0)\),其中 \(O\)为坐标原点,\(b>0\),若 \(A ,B ,C\)三点共线,则\(\dfrac{1}{a}+\dfrac{2}{b}\)的最小值为\(\underline{\quad \quad}\). 【解析】\(\overrightarrow{A B}=(a-1,1)\),\(\overrightarrow{A C}=(-b-1,2)\). \(∵A ,B ,C\) 三点共线,\(∴2(a-1)-(-b-1)=0\),化为\(2a+b=1\). 则\(\dfrac{1}{a}+\dfrac{2}{b}=(2 a+b)\left(\dfrac{1}{a}+\dfrac{2}{b}\right)\)\(=4+\dfrac{b}{a}+\dfrac{4 a}{b} \geq 4+2 \sqrt{\dfrac{b}{a} \cdot \dfrac{4 a}{b}}=8\), 当且仅当\(b=2 a=\dfrac{1}{2}\)时取等号. 【点拨】\(A ,B ,C\)三点共线,即\(\overrightarrow{A B} / / \overrightarrow{A C}\). 【典题3】 已知向量\(\vec{a}=(2,1)\),\(\vec{b}=(-1, m)\),若\(\vec{a}\)与\(\vec{b}\)夹角为钝角,则\(m\)的取值范围是\(\underline{\quad \quad}\). 【解析】 向量\(\vec{a}=(2,1)\),\(\vec{b}=(-1, m)\), 若\(\vec{a}\)与\(\vec{b}\)夹角为钝角,则\(\left\{\begin{array}{l} \vec{a} \cdot \vec{b} |
【本文地址】
 \({\color{Red}{PS}}\) 唯一性的解释
若\(\overrightarrow{e_{1}}\),\(\overrightarrow{e_{2}}\)不共线,且\(\lambda_{1} \overrightarrow{e_{1}}+\mu_{1} \overrightarrow{e_{2}}=\lambda_{2} \overrightarrow{e_{1}}+\mu_{2} \overrightarrow{e_{2}}\), 则\(λ_1=λ_2\) ,\(μ_1=μ_2\).
\({\color{Red}{PS}}\) 唯一性的解释
若\(\overrightarrow{e_{1}}\),\(\overrightarrow{e_{2}}\)不共线,且\(\lambda_{1} \overrightarrow{e_{1}}+\mu_{1} \overrightarrow{e_{2}}=\lambda_{2} \overrightarrow{e_{1}}+\mu_{2} \overrightarrow{e_{2}}\), 则\(λ_1=λ_2\) ,\(μ_1=μ_2\). 如上图,重力\(G\)分解成平行斜面的力\(F_1\)和垂直于斜面的压力\(F_2\).
如上图,重力\(G\)分解成平行斜面的力\(F_1\)和垂直于斜面的压力\(F_2\).
 【解析】以\(AB\)所在直线为\(x\)轴,以\(A\)为原点建立平面直角坐标系(如图).
【解析】以\(AB\)所在直线为\(x\)轴,以\(A\)为原点建立平面直角坐标系(如图).
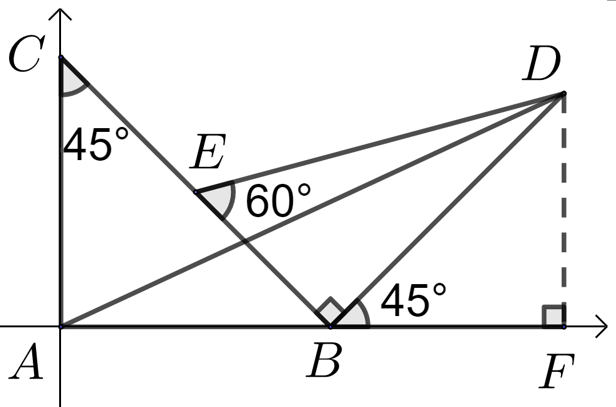 令\(AB=2\),则\(\overrightarrow{A B}=(2,0)\),\(\overrightarrow{A C}=(0,2)\)
过\(D\)作\(DF⊥AB\)交\(AB\)的延长线为\(F\),由已知得\(D E=B C=2 \sqrt{2}\),故\(DB=\sqrt{6}\),
则\(D F=B F=\sqrt{3}\),则\(\overrightarrow{A D}=(2+\sqrt{3}, \sqrt{3})\).
\(\because \overrightarrow{A D}=x \overrightarrow{A B}+y \overrightarrow{A C}\),\(\therefore(2+\sqrt{3}, \sqrt{3})=(2 x, 2 y)\).
即有\(x=1+\dfrac{\sqrt{3}}{2}\),\(y=\dfrac{\sqrt{3}}{2}\)
【点拨】
① 本题也可以用平行四边形法则求解;
② 这里讲解的方法是建系法,常见步骤如下
(1) 找到合适的方式(一般是利用题中垂直关系等)建系;
(2) 通过一些几何的知识点求出线段的长度,进而得到关键点的坐标;
(3) 关键向量用坐标形式表示,比如本题中的\(\overrightarrow{A B}=(2,0)\),\(\overrightarrow{A D}=(2+\sqrt{3}, \sqrt{3})\)等;
(4) 得到方程组求解(其实就是利用平面向量的基本定理的唯一性).
③ 当根据题意发现容易建系(比如有明显的垂直关系等),可考虑建系法,它充分体现了“解析几何的优势”.
令\(AB=2\),则\(\overrightarrow{A B}=(2,0)\),\(\overrightarrow{A C}=(0,2)\)
过\(D\)作\(DF⊥AB\)交\(AB\)的延长线为\(F\),由已知得\(D E=B C=2 \sqrt{2}\),故\(DB=\sqrt{6}\),
则\(D F=B F=\sqrt{3}\),则\(\overrightarrow{A D}=(2+\sqrt{3}, \sqrt{3})\).
\(\because \overrightarrow{A D}=x \overrightarrow{A B}+y \overrightarrow{A C}\),\(\therefore(2+\sqrt{3}, \sqrt{3})=(2 x, 2 y)\).
即有\(x=1+\dfrac{\sqrt{3}}{2}\),\(y=\dfrac{\sqrt{3}}{2}\)
【点拨】
① 本题也可以用平行四边形法则求解;
② 这里讲解的方法是建系法,常见步骤如下
(1) 找到合适的方式(一般是利用题中垂直关系等)建系;
(2) 通过一些几何的知识点求出线段的长度,进而得到关键点的坐标;
(3) 关键向量用坐标形式表示,比如本题中的\(\overrightarrow{A B}=(2,0)\),\(\overrightarrow{A D}=(2+\sqrt{3}, \sqrt{3})\)等;
(4) 得到方程组求解(其实就是利用平面向量的基本定理的唯一性).
③ 当根据题意发现容易建系(比如有明显的垂直关系等),可考虑建系法,它充分体现了“解析几何的优势”.
 【解析】 建立如图所示的坐标系,
【解析】 建立如图所示的坐标系,
 则\(A(0 ,0)\),\(B(2 ,0)\) ,\(D(0 ,1)\),\(C(2 ,2)\),\(E(2 ,1)\),\(F\left(1, \dfrac{3}{2}\right)\),
\(P(\cos α ,\sin α)\) \((0≤α≤π)\),
\({\color{Red}{(因为P在单位圆上,α为∠PAM)}}\)
由\(\overrightarrow{A P}=\lambda \overrightarrow{A E}+\mu \overrightarrow{B F}\)得\((\cos \alpha, \sin \alpha)\)\(=\lambda(2,1)+\mu\left(-1, \dfrac{3}{2}\right)=\left(2 \lambda-\mu, \lambda+\dfrac{3}{2} \mu\right)\)
\(\Rightarrow \cos \alpha=2 \lambda-\mu, \sin \alpha=\lambda+\dfrac{3}{2} \mu\)
\(\Rightarrow \lambda=\dfrac{3}{8} \cos \alpha+\dfrac{1}{4} \sin \alpha, \quad \mu=\dfrac{1}{2} \sin \alpha-\dfrac{1}{4} \cos \alpha\)
\(\therefore 2 \lambda-5 \mu\)\(=2\left(\dfrac{3}{8} \cos \alpha+\dfrac{1}{4} \sin \alpha\right)-5\left(\dfrac{1}{2} \sin \alpha-\dfrac{1}{4} \cos \alpha\right)\)
\(=-2(\sin \alpha-\cos \alpha)=-2 \sqrt{2} \sin \left(\alpha-\dfrac{\pi}{4}\right)\)
\(\because \alpha-\dfrac{\pi}{4} \in\left[-\dfrac{\pi}{4}, \dfrac{3 \pi}{4}\right]\) , \(\therefore-2 \sqrt{2} \sin \left(\alpha-\dfrac{\pi}{4}\right) \in[-2 \sqrt{2}, 2]\)
即\(2λ-5μ\)的取值范围是\([-2 \sqrt{2}, 2]\).
【点拨】 利用建系法求解,点\(P\)在单位圆上,巧妙的设为\(P(\cosα ,\sinα)\),引入参数\(α\),此处要注意\(0≤α≤π\),则\(2λ-5μ\)是\(α\)的函数,求最值不难了.
则\(A(0 ,0)\),\(B(2 ,0)\) ,\(D(0 ,1)\),\(C(2 ,2)\),\(E(2 ,1)\),\(F\left(1, \dfrac{3}{2}\right)\),
\(P(\cos α ,\sin α)\) \((0≤α≤π)\),
\({\color{Red}{(因为P在单位圆上,α为∠PAM)}}\)
由\(\overrightarrow{A P}=\lambda \overrightarrow{A E}+\mu \overrightarrow{B F}\)得\((\cos \alpha, \sin \alpha)\)\(=\lambda(2,1)+\mu\left(-1, \dfrac{3}{2}\right)=\left(2 \lambda-\mu, \lambda+\dfrac{3}{2} \mu\right)\)
\(\Rightarrow \cos \alpha=2 \lambda-\mu, \sin \alpha=\lambda+\dfrac{3}{2} \mu\)
\(\Rightarrow \lambda=\dfrac{3}{8} \cos \alpha+\dfrac{1}{4} \sin \alpha, \quad \mu=\dfrac{1}{2} \sin \alpha-\dfrac{1}{4} \cos \alpha\)
\(\therefore 2 \lambda-5 \mu\)\(=2\left(\dfrac{3}{8} \cos \alpha+\dfrac{1}{4} \sin \alpha\right)-5\left(\dfrac{1}{2} \sin \alpha-\dfrac{1}{4} \cos \alpha\right)\)
\(=-2(\sin \alpha-\cos \alpha)=-2 \sqrt{2} \sin \left(\alpha-\dfrac{\pi}{4}\right)\)
\(\because \alpha-\dfrac{\pi}{4} \in\left[-\dfrac{\pi}{4}, \dfrac{3 \pi}{4}\right]\) , \(\therefore-2 \sqrt{2} \sin \left(\alpha-\dfrac{\pi}{4}\right) \in[-2 \sqrt{2}, 2]\)
即\(2λ-5μ\)的取值范围是\([-2 \sqrt{2}, 2]\).
【点拨】 利用建系法求解,点\(P\)在单位圆上,巧妙的设为\(P(\cosα ,\sinα)\),引入参数\(α\),此处要注意\(0≤α≤π\),则\(2λ-5μ\)是\(α\)的函数,求最值不难了.
 A.满足\(λ+μ=2\)的点\(P\)必为\(BC\)的中点
B.满足\(λ+μ=1\)的点\(P\)有且只有一个
C.满足\(λ+μ=a(a>0)\)的点\(P\)最多有\(3\)个
D.\(λ+μ\)的最大值为\(3\)
A.满足\(λ+μ=2\)的点\(P\)必为\(BC\)的中点
B.满足\(λ+μ=1\)的点\(P\)有且只有一个
C.满足\(λ+μ=a(a>0)\)的点\(P\)最多有\(3\)个
D.\(λ+μ\)的最大值为\(3\)