卡方分布怎么理解？

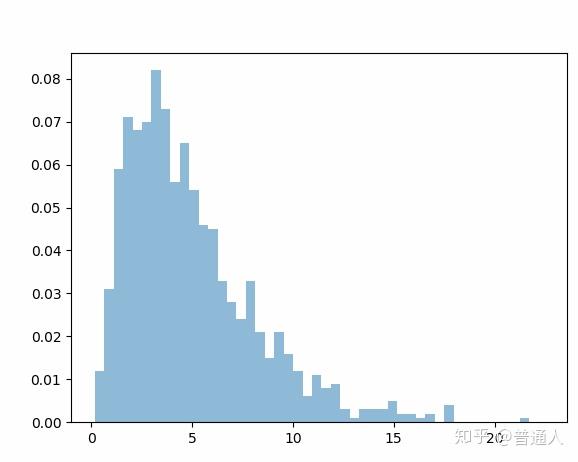而早期研究中心极限定理（那个时候的中心极限定理证明不是用的现代数学证明）的数学家斯特林得出了n！的近似值（这个时候的近似值还是基于整数）而之前研究数列牛顿插值公式来确定近似函数（如泰勒公式）数学家想能否用插值得出一个阶乘的近似函数，于是经过数学家的不懈努力最后确定了积分形式下的伽马函数将阶乘扩展到实数域上（说实话每当我去了解数学史时由衷的钦佩这些数学家）于是得出了大名鼎鼎的伽马函数。

第二个是证明自由度为1的卡方分布

第三个用卷积公式证明多个卡方样本连加下的结果

之后卡方分布概率密度的一般形式的公式就可以证明出来:

我们这里也可以随机模拟一下随机变量服从正态分布不同下的自由度卡方频率分布图。

自由度为1

自由度为2

自由度为5

很明显和概率论不同自由度下的密度曲线是很吻合的：

这里的自由度要理解的话可以参考无偏估计，其中方差的的无偏估计是最经典的，我这里只提及一下，有兴趣研究的可以深入查阅资料。

以上是方差的无偏估计。这也是为啥我们估计方差的时候要减去1/n个方差，所以方差的无偏估计自由度为n-1

好了得到这个公式有什么用，之所以要摆出卡方概率密度函数是用来做假设检验的（我们后面再说），在数学中我们知道如果A，B两个事件独立那么P(AB)=P(A)*P(B)，我们高中如果接触的是人教版的数学中，数学书中肯定有列联表这个东西。

如果相互独立那理论上可以得出P(男同时喜欢逛街)如下：

P（男）=52/87 P（喜欢逛街）=87/100

P(男同时喜欢逛街)= P（男）* P（喜欢逛街）

如果列联表共有 r 行 c 列，那么在独立事件的假设下，每个字段的“理论次数”（或期望次数）为：

我们之前在文章中是提出了一下两个公式的

所以（参考维基百科上如下得出了一个卡方的统计值）

自由度=(r-1)(c-1)

那我们有了卡方分布的概率密度曲线可以用来假设检验了，如下图我们知道概率是概率密度曲线下的面积（积分计算）我们画线的地方也就是卡方分布的随机变量小于等于这条线的概率为95%，如果你的卡方随机变量超过了这条线发生的概率为小概率事件，我们可以假定为不可能事件。

我们计算机模拟计算一下（代码如下）：

# -*- coding: UTF-8 -*-

import numpy as np

import matplotlib.pyplot as plt

import random

from copy import deepcopy

import scipy as sy

from scipy.stats import chi2 #导入卡方分布常见需要的包

from scipy.stats import norm

from scipy import integrate #某些包需要单独的导入

from sympy.integrals.transforms import mellin_transform

from sympy import exp

from sympy.abc import x, s

from scipy.special import gamma

#数学带符号运算库---考虑性能暂时不启用

#import sympy as smy

def fxNormal(x,sigma,mu):

'''

正态分布的密度函数

:param x: 随机变量

:param sigma: 标准差

:param mu: 均值

:return: 返回正态分布的密度函数计算过的值（区间上的积分才是概率）

'''

left=1 / (sigma * np.sqrt(2 * np.pi))

right=np.exp(- (x - mu) ** 2 / (2 * sigma ** 2))

result=left*right

return result;

def getNormalXY(xmin,xmax,step ,sigma,mu):

'''

分布调用函数

x,y=getNormalXY(-100,100,0.01,1,0)

plt.xlim(-2,2)

plt.plot(x,y);

plt.show()

:param xmin: 最小的x值

:param xmax: 最大的x值

:param step: 描点分割

:param sigma: 标准差

:param mu: 均值

:return: 返回区间描点的图

'''

x = np.arange(xmin, xmax, step);

y = []

for xi in x:

y.append(fxNormal(xi,sigma,mu))

return x,y

def drawDistribution():

'''

标准化分布的检验

:return:

'''

mu, sigma = 0, 1 # mean and standard deviation

#产生正态分布的随机数 r = norm.rvs(size=1000) 等同

s = np.random.normal(mu, sigma, 10000)

#和标准正态分布的均值比较

print(abs(mu - np.mean(s)))

#和正态分布的标准差做比较---这里ddof表示的是自由度

print(abs(sigma - np.std(s, ddof=1)))

#得到计数，区间

count, bins, ignored = plt.hist(s, 30, normed=True)

plt.plot(bins,fxNormal(bins,sigma,mu),linewidth=2, color='r')

plt.show()

def takeArrayValue(arr,n):

'''

随机放回抽样拿取数组n次

:param arr: 抽样数据的数组

:param n: 次数

:return: 返回抽样好的数组

'''

max=arr.__len__()-1;

resultArr=[]

while n>0:

index=random.randint(0,max)

resultArr.append(arr[index])

n=n-1

return resultArr

def chiSquareDistribution(chiSquareNum,n):

'''

生成卡方分布

:param chiSquareNum: 生成卡方随机数个数

:param n: 卡方分布随机数n值

:return: 返回生成卡方分布随机的大小

'''

chiSquareDisArr=[]

for i in range(chiSquareNum):

# 产生正态分布的随机数

randomNormalArr = np.random.normal(0, 1, n)

#将卡方值加入数组

chiSquareDisArr.append(np.sum(randomNormalArr*randomNormalArr))

return chiSquareDisArr

def draw_hist(limit_distribution):

'''

卡方检验的直方图绘制

:param limit_distribution: 分布数组

:return:

'''

minx=min(limit_distribution)

print(minx)

maxx=max(limit_distribution)

difference=maxx-minx

segmentation=difference/300

bins = np.arange(minx,maxx,segmentation) # 固定落区域

# 限制x轴范围

plt.xlim((-1,minx+difference))

#直接按照直方图频率显示，而不是频数

plt.hist(limit_distribution, bins=bins,weights=[1.0/ len(limit_distribution)] * len(limit_distribution), alpha=0.5)

#plt.plot(bins,chiSquareFunc(100,bins), linewidth=2, color='r')

plt.show()

# def gammaIntegral(s):

# '''

# 计算伽马函数积分值

# :param s: 伽马含参量变量

# :param integralCeiling: 积分上限

# :return:

# '''

# # # 第一种计算伽马函数办法

# # gama = lambda x: sy.exp(-x) * sy.power(x, s - 1)

# # print(integrate.quad(gama, 0, sy.inf))#返回积分值 返回误差

# # #第二种计算伽马函数的办法

# # print(mellin_transform(exp(-x), x, s))

# #第三种直接调用伽马函数库

# #gamma(5)

# result=mellin_transform(exp(-x), x, s)

# return result[0]

# def chiSquareFunc(n,y):

# '''

# 卡方分布的概率密度函数

# :param n: 自由度

# :param y: 函数变量值数组

# :return: 返回概率密度计算的具体值按传入变量数组计算

# '''

# result = 0

# if y > 0:

# #result =1/ (sy.power(2, n / 2) * gamma(n / 2))* sy.power(y, n / 2 - 1) * sy.exp(-y / 2)

# #等同于调用一下函数---chi2.pdf(0.01,1)

# result =1 / (np.power(2,n/2)*gamma(n/2)) * (y)**(n/2-1) * exp(-y/2)

# return result

# print(chi2.pdf(0.01,1))

def draw_chi(n):

'''

卡方分布曲线图

:param n:

:return:

'''

chiarr=np.linspace(0,50,1000)

plt.plot(chiarr, chi2.pdf(chiarr,n), linewidth=2, color='r')

plt.show()

def chiSquareDistTest(n):

'''

测试方法，用来测试卡方频率分布的,得到卡方图

:param n: 自由度

:return:

'''

limit_distribution=chiSquareDistribution(10000,n)

draw_hist(limit_distribution)

if __name__ == '__main__':

#绘制卡方分布密度曲线

#draw_chi(1)

#绘制卡方分布概率频率图

#chiSquareDistTest(5)

#cdf(x, df, loc=0, scale=1)

#计算分位点

print(chi2.ppf(0.95,1))

可以看到自由度为1时的分位点为3.84145882069

而计算的卡方值为1.77，我们有充分理由无法说明这个两个类别不相互独立。

所以卡方检验在数理统计中占有及其重要的作用，接下来我们还会用到这个写另外几篇单身狗系列。

参考文章：

（皮尔森卡方检验）

http://www.flickering.cn/%E6%95%B0%E5%AD%A6%E4%B9%8B%E7%BE%8E/2014/06/%E7%A5%9E%E5%A5%87%E7%9A%84%E4%BC%BD%E7%8E%9B%E5%87%BD%E6%95%B0%E4%B8%8A/

（卡方检验）

https://zh.wikipedia.org/wiki/卡方检验

（神奇的伽马函数）

http://www.flickering.cn/%E6%95%B0%E5%AD%A6%E4%B9%8B%E7%BE%8E/2014/06/%E7%A5%9E%E5%A5%87%E7%9A%84%E4%B

该文章来自：